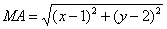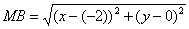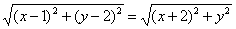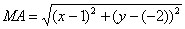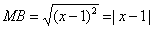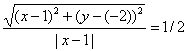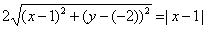Пример №1 . Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как
то
После возведения левой и правой частей в квадрат и упрощений получим:
(x-1) 2 + (y-2) 2 = (x + 2) 2 + y 2
x 2 — 2x + 1 + y 2 — 4y + 4 = x 2 + 4x + 4 + y 2
или
— 6x — 4y + 1 = 0
Ответ: — 6x — 4y + 1 = 0.
Пример №2 .
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1 /2.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1 /2. Так как:
то
или
Возведя левую и правую части в квадрат и упрощая, получим:
4(x — 1) 2 + 4(y + 2) 2 = |x — 1| 2
т.е.
4(x 2 — 2x + 1) + 4(y 2 + 4y + 4) = x 2 — 2x + 1
или
3x 2 + 4y 2 — 6x +16y +19 = 0
Ответ: 3x 2 + 4y 2 — 6x +16y +19 = 0.
Пример №3 . Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4 .
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.
Пример №4 . Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6 , λ=1.
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать
Составить уравнение множества точек,равноудаленных от двух данных точек М1 (-4;3) и
Составить уравнение множества точек,равноудаленных от 2-ух данных точек М1 (-4;3) и М2(2;5).
- София Полинко
- Математика 2019-10-09 09:56:41 0 1
1. Расстояние меж точками с координатами A1(x1; y1) и A2(x2, y2) определяется формулой:
A1A2 = ((x2 — x1)^2 + (y2 — y1))^2. (1)
2. Исходя из формулы (1), составим уравнение огромного количества точек, равноудаленных от 2-ух данных точек М1(-4; 3) и М2(2; 5):
- (x + 4)^2 + (y — 3)^2 = (x — 2)^2 + (y — 5)^2;
- x^2 + 8x + 16 + y^2 — 6y + 9 = x^2 — 4x + 4 + y^2 — 10y + 25;
- 8x — 6y + 25 = -4x — 10y + 29;
- 12x + 4y — 4 = 0;
- 3x + y — 1 = 0;
- y = 1 — 3x. (2)
3. Как видно из уравнения (2), обильем всех точек является ровная с угловым коэффициентом -3.
Видео:Составляем уравнение прямой по точкамСкачать
Составить уравнение множества точек,равноудаленных от двух данных точек М1 (-4;3) и
Составить уравнение множества точек,равноудаленных от двух данных точек М1 (-4;3) и М2(2;5).
1. Расстояние между точками с координатами A1(x1; y1) и A2(x2, y2) определяется формулой:
A1A2 = √((x2 — x1)^2 + (y2 — y1))^2. (1)
2. Исходя из формулы (1), составим уравнение множества точек, равноудаленных от двух данных точек М1(-4; 3) и М2(2; 5):
- (x + 4)^2 + (y — 3)^2 = (x — 2)^2 + (y — 5)^2;
- x^2 + 8x + 16 + y^2 — 6y + 9 = x^2 — 4x + 4 + y^2 — 10y + 25;
- 8x — 6y + 25 = -4x — 10y + 29;
- 12x + 4y — 4 = 0;
- 3x + y — 1 = 0;
- y = 1 — 3x. (2)
3. Как видно из уравнения (2), множеством всех точек является прямая с угловым коэффициентом -3.
📽️ Видео
Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Уравнения стороны треугольника и медианыСкачать
Найти точку пересечения прямой и плоскостиСкачать
Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
Математика без Ху!ни. Уравнение плоскости.Скачать
18. Расстояние от точки до прямой в пространствеСкачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Видеоурок "Канонические уравнения прямой"Скачать
9 класс, 2 урок, Множества и операции над нимиСкачать
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать
Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
Уравнение плоскости. 11 класс.Скачать
Множества и операции над нимиСкачать
