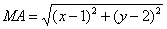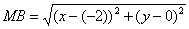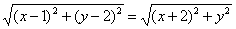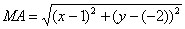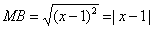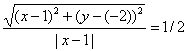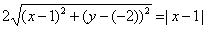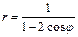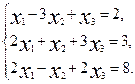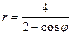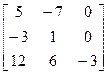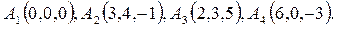Составить уравнение множества точек расстояние которых от точки a 0 1 в два раза меньше

Пример №1 . Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как


то

После возведения левой и правой частей в квадрат и упрощений получим:
(x-1) 2 + (y-2) 2 = (x + 2) 2 + y 2
x 2 — 2x + 1 + y 2 — 4y + 4 = x 2 + 4x + 4 + y 2
или
— 6x — 4y + 1 = 0
Ответ: — 6x — 4y + 1 = 0.

Пример №2 .
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1 /₂.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1 /₂. Так как:


то

или

Возведя левую и правую части в квадрат и упрощая, получим:
4(x — 1) 2 + 4(y + 2) 2 = |x — 1| 2
т.е.
4(x 2 — 2x + 1) + 4(y 2 + 4y + 4) = x 2 — 2x + 1
или
3x 2 + 4y 2 — 6x +16y +19 = 0
Ответ: 3x 2 + 4y 2 — 6x +16y +19 = 0.

Пример №3 . Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4 .
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.

Пример №4 . Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6 , λ=1.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Составить уравнение линии, для каждой точки которой расстояние до точки А (0 ; 1) вдвое меньше расстояния до прямой y = 4 ?

Математика | 10 — 11 классы

Составить уравнение линии, для каждой точки которой расстояние до точки А (0 ; 1) вдвое меньше расстояния до прямой y = 4 .

Пусть М(Xm ; Ym) — точка искомой линии, уравнение которой мы ищем.

Мы знаем, что расстояние между точками А и М — это модуль вектора АМ, координаты которого находятся, как разность координат его конца и начала.

Итак, |АМ| = √[(Xm — Xa)² + (Ym — Ya)²] = √[Xm² + (Ym — 1)²].

Формула расстояния от точки до прямой, заданной уравнением прямой АХ + ВY + C = 0 имеет вид : d = |A * Xm + B * Ym + C| / √(A² + B²).

В нашем случае d = |Ym — 4| / 1 = |Ym — 4|.

По условию 2 * |АМ| = |Ym — 4|.

То есть 2√[Xm² + (Ym — 1)²] = Ym — 4 или, если возвести в квадрат обе части уравнения,

4(Xm² + Ym² — 2Ym + 1) = Ym² — 8Ym + 16 = &gt ; 4Xm² + 3Ym² = 12 или

Xm² / 3 + Ym² / 4 = 1.

А это — каноническое уравнение эллипса.

Его полуоси а = √3 и b = 2.

Видео:Составляем уравнение прямой по точкамСкачать

На гиперболе 9х² — 16у² = 144 найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого?

На гиперболе 9х² — 16у² = 144 найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Проведите прямую a (не по линиям сетки)?

Проведите прямую a (не по линиям сетки).

На прямой а отметьте точку С.

Через точку С проведите прямую б, перпендикулярную прямой а.

Отметьте точку D, не лежащую на прямых а и b.

Измерьте и запишите расстояние от точки D до прямой b.

Видео:Уравнение окружности (1)Скачать

Найдите расстояние от точки А(4, 3) до точки с наименьшей целой координатой, модуль который меньше координаты точки А?

Найдите расстояние от точки А(4, 3) до точки с наименьшей целой координатой, модуль который меньше координаты точки А.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Точки А, В и С лежат на одной прямой?

Точки А, В и С лежат на одной прямой.

Расстояние между точками А и В равно 10 см, а между точками В и С — 3 см.

Найдите расстояние между точками А и С.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Определить уравнение траектории точки M(x?

Определить уравнение траектории точки M(x.

Y), которая движется так, что ее расстояние от точки F( — 1.

0) остается вдвое меньше расстояния от прямой x = — 4.

Видео:9 класс, 2 урок, Множества и операции над нимиСкачать

Помогите пожалуйста?

Через точку В, отстаящую на 5 см от цента О окружности, проведена прямая, которая касается этой окружности в точке А.

Найдите расстояние от точки В до точки С.

В которой прямая Во пересекает окружность, учитывая, что АВ = 4 см.

Видео:Задачи на движение. Учимся решать задачи на движение. Способы решения задач на движение.Скачать

Прямая а пересекает отрезок kl в его середине точка b?

Прямая а пересекает отрезок kl в его середине точка b.

Найдите расстояние от точки k до прямой а, если расстояние от точки l до этой прямой 55 см.

Видео:7 класс, 11 урок, Смежные и вертикальные углыСкачать

Расстояние между двумя точками прямой?

Расстояние между двумя точками прямой.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Линия все точки которой находятся на одном и том же расстоянии от точки называемой центром 10 букв?

Линия все точки которой находятся на одном и том же расстоянии от точки называемой центром 10 букв.

Видео:Решение неравенства методом интерваловСкачать

Расстояние от точки до прямой -?

Расстояние от точки до прямой -.

Вы открыли страницу вопроса Составить уравнение линии, для каждой точки которой расстояние до точки А (0 ; 1) вдвое меньше расстояния до прямой y = 4 ?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

задача по математике Составить уравнение линии, расстояние каждой точки которой от точкиF(0; −1) втрое меньше, чем

Составить уравнение линии, расстояние каждой точки которой от точки
F(0; -1) втрое меньше, чем от прямой y — 36 = 0. Сделать чертеж.

меня интересует как составить уравнение

Решение с рисунком отправил на почту. Возможность разместить тут ограничена.

Видео:Движение тела, брошенного под углом к горизонтуСкачать

Контрольная работа №1 3 страница

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.

А =

Найти пределы функции, не пользуясь правилом Лопиталя.

а)	в)
б)	г)

Дано комплексное число z = -6 / (1- i ). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w 3 +z =0.

Вариант 15

Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.

Даны векторы a (1; 2; 1), b (2; -1; 3), c (3; -1; 4), d (5; 1; 6) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.

Найти:1)длину ребра А₁А₂; 2)угол между ребрами А₁А_{2 И} А₁А₄; 3)угол между ребром А₁А₄ и гранью А₁А₂А₃; 4)площадь грани А₁А₂А₃; 5)объем пирамиды; 6)уравнение прямой А₁А_2; 7)уравнение плоскости А₁А₂А₃; 8)уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертеж.

Дана вершина треугольника А (3; 9) и уравнения медиан: y – 6 = 0; 3x – 4y + 9 = 0. Найти координаты двух вершин. Сделать чертеж.

Написать уравнение множества точек, одинаково удаленных от точки F (0; 2) и прямой y = 4. Найти точки пересечения этой кривой с осями координат и построить ее.

Линия задана уравнением в полярной системе координат

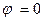
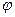
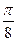
Требуется:1)построить линию по точкам, начиная от до и придавая значения через промежуток ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

Даны два линейных преобразования:

Средствами матричного исчисления найти преобразование, выражающее x // ₁, x // ₂, x // ₃ через x₁, x₂, x₃.

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.

А =

Найти пределы функции, не пользуясь правилом Лопиталя.

а)	в)
б)	г)

Дано комплексное число z = 3 / ( 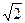+i). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w 3 +z =0.

Вариант 16

Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.

Даны векторы a (5; 2; 1), b (8; -3; 2), c (-1; 2; 3), d (7; 9; 1) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.

Найти:1)длину ребра А₁А₂; 2)угол между ребрами А₁А_{2 И} А₁А₄; 3)угол между ребром А₁А₄ и гранью А₁А₂А₃; 4)площадь грани А₁А₂А₃; 5)объем пирамиды; 6)уравнение прямой А₁А₂ ; 7)уравнение плоскости А₁А₂А₃; 8)уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертеж.

Даны стороны треугольника: x – y + 2 = 0 (AB), x = 2 (BC), x + y – 2 = 0 (AC). Составить уравнение прямо, проходящей через вершину В и через точку на стороне АС, делящую ее (считая от вершины А) в отношении 1:3. Сделать чертеж.

Найти уравнение множества точек, равноотстоящих от окружности x 2 + 4x + y 2 = 0 и от точки М (2; 0).

Линия задана уравнением в полярной системе координат

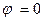
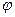
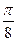
Требуется:1)построить линию по точкам, начиная от до и придавая значения через промежуток ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

Даны два линейных преобразования:

Средствами матричного исчисления найти преобразование, выражающее x // ₁, x // ₂, x // ₃ через x₁, x₂, x₃.

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.

А =

Найти пределы функции, не пользуясь правилом Лопиталя.

а)	в)
б)	г)

Дано комплексное число z = 3 / ( 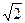— I). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w 3 +z =0.

Вариант 17

Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.

Даны векторы a (1; 2; 3), b (-2; 3; -2), c (3; -4; -5), d (6; 20; 6) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.

Найти:1)длину ребра А₁А₂; 2)угол между ребрами А₁А_{2 И} А₁А₄; 3)угол между ребром А₁А₄ и гранью А₁А₂А₃; 4)площадь грани А₁А₂А₃; 5)объем пирамиды; 6)уравнение прямой А₁А₂ ; 7)уравнение плоскости А₁А₂А₃; 8)уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертеж.

Найти уравнение прямой, проходящей через точку (-1; 1) так чтобы середина ее отрезка между прямыми x + 2y – 1 = 0 и x + 2y – 3 = 0 лежала на прямой x – y – 1 = 0. Сделать чертеж.

Составить уравнение множества точек, расстояния которых от точки А (0; 1) в два раза меньше расстояния до прямой у – 4 = 0.

Линия задана уравнением в полярной системе координат

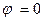
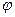
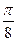
Требуется:1)построить линию по точкам, начиная от до и придавая значения через промежуток ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

Даны два линейных преобразования:

Средствами матричного исчисления найти преобразование, выражающее x // ₁, x // ₂, x // ₃ через x₁, x₂, x₃.

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.

А =

Найти пределы функции, не пользуясь правилом Лопиталя.

а)	в)
б)	г)

Дано комплексное число z = 6 / ( +i). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w 3 +z =0.

Вариант 18

Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.

Даны векторы a (4; 2; 5), b (-3; 5; 6), c (2; -3; -2), d (8; 11; 13) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.

Найти:1)длину ребра А₁А₂; 2)угол между ребрами А₁А_{2 И} А₁А₄; 3)угол между ребром А₁А₄ и гранью А₁А₂А₃; 4)площадь грани А₁А₂А₃; 5)объем пирамиды; 6)уравнение прямой А₁А₂; 7)уравнение плоскости А₁А₂А₃; 8)уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертеж.

В треугольнике АВС даны: уравнение стороны АВ 3x + 2y = 12, уравнение высоты ВМ x +2y = 4, уравнение высоты АМ 4x + y = 6, где М – точка пересечения высот. Написать уравнения сторон АС, ВС и высоты СМ. Сделать чертеж.

Дана окружность x 2 + y 2 =4. Из точки А (-2; 0) проведена хорда АВ, которая продолжена на расстояние |ВМ| = |АВ|. Найти множество точек М.

Линия задана уравнением в полярной системе координат

Требуется:1)построить линию по точкам, начиная от до и придавая значения через промежуток ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

Даны два линейных преобразования:

Средствами матричного исчисления найти преобразование, выражающее x // ₁, x // ₂, x // ₃ через x₁, x₂, x₃.

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.

А =

Найти пределы функции, не пользуясь правилом Лопиталя.

а)	в)
б)	г)

Дано комплексное число z = -6 / ( +i). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w 3 +z =0.

Вариант 19

Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.

Даны векторы a (1; 3; 2), b (-2; 3; -2), c (3; -4; -5), d (6; 20; 6) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.

Найти:1)длину ребра А₁А₂; 2)угол между ребрами А₁А_{2 И} А₁А₄; 3)угол между ребром А₁А₄ и гранью А₁А₂А₃; 4)площадь грани А₁А₂А₃; 5)объем пирамиды; 6)уравнение прямой А₁А₂; 7)уравнение плоскости А₁А₂А₃; 8)уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертеж.

Две стороны параллелограмма заданы уравнениями у = x – 2 и 5у = x + 6. Диагонали его пересекаются в начале координат. Написать уравнения двух других сторон параллелограмма и его диагоналей. Сделать чертеж.

Составить уравнение линии, для каждой точки которой отношение расстояния от точки F (2; 0) к расстоянию до прямой x = 3 равно . Сделать чертеж.

Линия задана уравнением в полярной системе координат

Требуется:1)построить линию по точкам, начиная от до и придавая значения через промежуток ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

Даны два линейных преобразования:

Средствами матричного исчисления найти преобразование, выражающее x // ₁, x // ₂, x // ₃ через x₁, x₂, x₃.

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.

А =

Найти пределы функции, не пользуясь правилом Лопиталя.

а)	в)
б)	г)

Дано комплексное число z = -1 / (i+ ). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w 3 +z =0.

Вариант 20

Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.

Даны векторы a (1; 3; 2), b (3; -1; 5), c (-6; 5; -3), d (12; -10; 6) внекотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.

Найти:1)длину ребра А₁А₂; 2)угол между ребрами А₁А_{2 И} А₁А₄; 3)угол между ребром А₁А₄ и гранью А₁А₂А₃; 4)площадь грани А₁А₂А₃; 5)объем пирамиды; 6)уравнение прямой А₁А₂ ; 7)уравнение плоскости А₁А₂А₃; 8)уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертеж.

Написать уравнения сторон треугольника, зная одну его вершину А (0; 2) и уравнения высот ВМ x + y = 4 и СМ y = 2x, М – точка пересечения высот. Сделать чертеж.

Составить уравнение линии, для каждой точки которой расстояние до начала координат и до точки А (0; 5) относятся как 3:2. Сделать чертеж.

Линия задана уравнением в полярной системе координат

Требуется:1)построить линию по точкам, начиная от до и придавая значения через промежуток ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

Даны два линейных преобразования:

Средствами матричного исчисления найти преобразование, выражающее x // ₁, x // ₂, x // ₃ через x₁, x₂, x₃.

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.

А =

Найти пределы функции, не пользуясь правилом Лопиталя.

а)	в)
б)	г)

Дано комплексное число z = / (1-i ). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w 3 +z =0.

Вариант 21

Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.

Даны векторы a(3,-2,1), b(-1,1,-2), c(2,1,-3), и d(11,-6,5).в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.

Даны координаты вершины пирамиды А₁А₂А₃А₄:

Найти:1)длину ребра А₁А₂; 2)угол между ребрами А₁А_{2 И} А₁А₄; 3)угол между ребром А₁А₄ и гранью А₁А₂А₃; 4)площадь грани А₁А₂А₃; 5)объем пирамиды; 6)уравнение прямой А₁А₂ ; 7)уравнение плоскости А₁А₂А₃; 8)уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертеж.

Составить уравнения прямых проходящих через вершины треугольника А(5;-4), В(-1;3), С(-3,-2) параллельно противоположным сторонам. Сделать чертеж.

Написать уравнение траектории точки М(x; y),которая при своем движении остается втрое дальше от точки А(0;9), чем от точки В(0;2). Сделать чертеж.

Линия задана уравнением в полярной системе координат

Требуется:1)построить линию по точкам, начиная от до и придавая значения через промежуток ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

Дата добавления: 2014-12-30 ; просмотров: 53 ; Нарушение авторских прав

💥 Видео

Множества. Операции над множествами. 10 класс алгебраСкачать

Множества и операции над нимиСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

Множество. Элементы множества. 5 класс.Скачать

Математика без Ху!ни. Теория вероятностей, комбинаторная вероятность.Скачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать