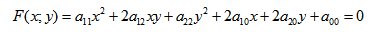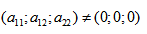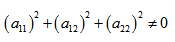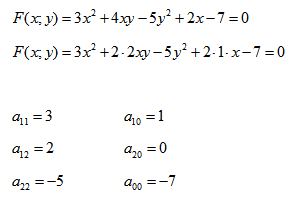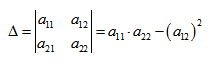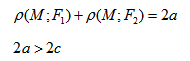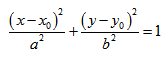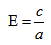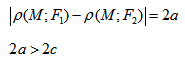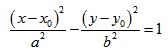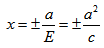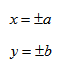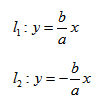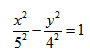Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
- Эллипс
- Гипербола
- Кривые второго порядка на плоскости
- Расчет кривой второго порядка на плоскости по точкам
- ИНВАРИАНТЫ И СВОДНАЯ ТАБЛИЦА
- Пример:
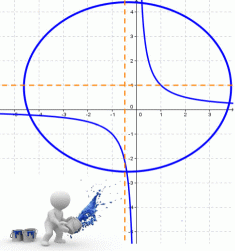
- Кривые второго порядка
- Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
- Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
- Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
- Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
- 🔍 Видео
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Эллипс
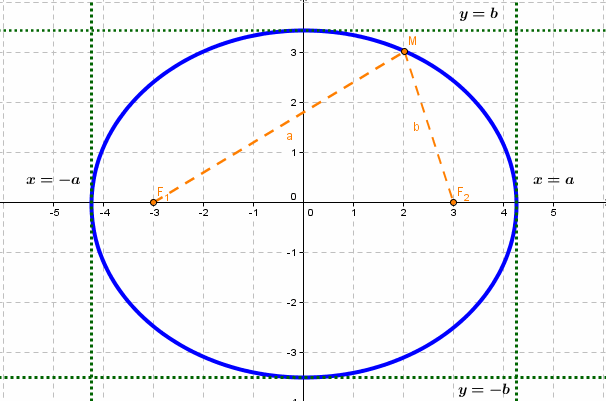
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Видео:Уравнение прямой по двум точкамСкачать

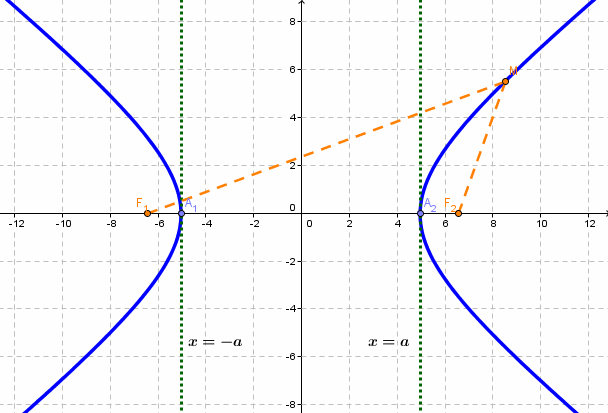
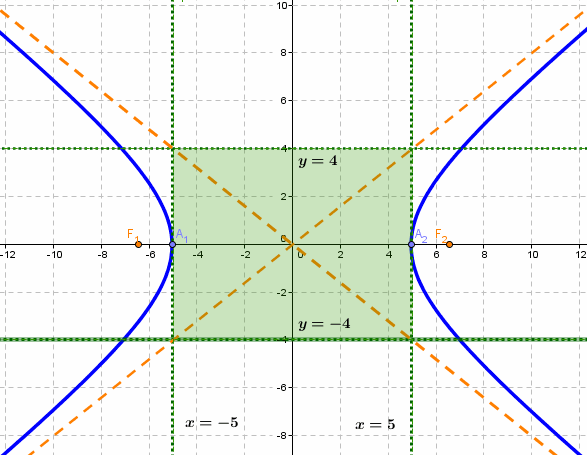
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 



Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию




Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Расчет кривой второго порядка на плоскости по точкам
| Элементы кривой второго порядка или координаты |
| Уравнения Ax^2+By^2+Cxy+Dx+Ey+F=0 |
| A= |
| B= |
| C= |
| D= |
| E= |
| F= |
| Полученная формула | ||||||||||||||||||||||
| Коэффициенты через пробел Калькулятор предназначен для расчета и создания уравнения кривых второго порядка на декартовой плоскости по нескольким точкам, от двух до пяти. Не является секретом то, что уравнение кривой второго порядка может быть представлена формулой Мы будем использовать чуть измененную формулу, разделив все коэффициенты на a6 отсюда видно, что кривую второго порядка можно однозначно определить по пяти точкам. Кривая второго порядка при различных коэффициентах может превращатся в следующие «типы»: — пара пересекающихся прямых — пара паралельных несовпадающих прямых — пары совпадающих прямых — линии, вырождающиеся в точку — «нулевые линии», то есть «линии», вовсе не имеющие точек Если Вам интересны формулы при которых получаются все эти типы, то пожалуйста — пара пересекающихся прямых — пара параллельных прямых — пара совпадающих прямых Этот сервис позволяет Вам по заданным точкам определить, какую же кривую второго порядка провести через эти точки. Кроме этого, Вы увидите все основные параметры полученной кривой второго порядка. От Вас лишь понадобится предоставить боту от двух до пяти декартовых координат, что бы бот мог решить эту задачу. Видео:Видеоурок "Общее уравнение кривой 2 порядка"Скачать  ИНВАРИАНТЫ И СВОДНАЯ ТАБЛИЦАЛюбая кривая второго порядка характеризуется тремя инвариантами, имеющими вид И одним семиинвариантом если Вам интересно, откуда они появились, то рекомендуем прочитать книгу «Аналитическая геометрия — Делоне» Характеристическое уравнение кривой второго порядка: Таким образом сводная таблица имеет вид
Анализируя написанные онлайн калькуляторы по этой теме, нашел интересную «особенность». Попробовав рассчитать по трем точкам кривую второго порядка, зная что эти точки принадлежат окружности, я с завидным постоянством получал ответ, что графиком(формой)полученного уравнения кривой является эллипс. Нет формально, конечно стоит признать что окружность является частным примером эллипса, но ведь можно пойти дальше и признать что и эллипс и гипербола и парабола, являются лишь частным примером кривой второго порядка общего вида, и в ответах таких калькуляторов выдавать ответ пользователю «вы получили уравнение второго порядка» и всё. не соврали же. Такое сверхлегкое трактование и смешение определений геометрических фигур, никак не способствует пониманию и сути решаемых задач. Это как в анекдоте «А теперь нарисуем квадрат со сторонами 3 на 4″(с) И не поймешь то ли рисовать квадрат, то ли прямоугольник. Видео:Приводим уравнение кривой 2 порядка к каноническому видуСкачать  Пример:Начнем сразу с проверочного примера Вообще, убедимся правильно ли считает бот? Итак, есть у нас функция x*x+3x-11=y определим значения при x=1,2,3,4,5 значения получились такие y=-7,-1,7,17,29 и зададим эти точки в качестве исходных пишем kp2 1:-7 2:-1 3:7 4:17 5:29 в результате получаем следующее: На первый взгляд получилось далеко не то, что должно получится. Но если мы уберем нулевые коэффициенты, и разделим все на 0.09091 то результат будет такой то есть Что и требовалось доказать в качестве правильности расчетов нашего бота. Теперь пусть у нас есть всего лишь три точки С координатами x=1,2,3 и y=-7,-1,7 Логично, что это тоже самое уравнение параболы что мы разбирали в первом примере. НО! при трех точках такое решение не единственное. Давайте попробуем задать боту всего три координаты и скажем ему какого вида уравнение мы хотим получить. Это частное уравнение кривой второго порядка в котором коэффициенты а1 и а5 равны нулю Скажем об этом боту kp2 0 1:-7 2:-1 3:7 0 1 где 0- показывает какие коэффициенты нам НЕ надо учитывать, а 1 — это постоянный коэффициент, то есть его находить нет необходимости. Он известен. Видим что не учитываем 1 и 5 коэффициент. Кривая второго порядка a1*x*x+a2*y*y+a3*x*y+a4*x+a5*y+a6 = 0 Видео:Кривые второго порядкаСкачать  Кривые второго порядкаВидео:§31.1 Приведение уравнения кривой к каноническому видуСкачать  Видео:Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать  Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:Видео:Приведение кривой второго порядка к каноническому виду. ПримерСкачать  Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать  Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.Видео:53. Приведение общего уравнения кривой к каноническому видуСкачать  или можно встретить следующую форму записи: Видео:Составляем уравнение прямой по точкамСкачать  К кривым второго порядка относятся окружность, эллипс, гипербола и парабола. Покажем на примере определение значений коэффициентов. Рассмотрим кривую второго порядка: Видео:11. Прямая в пространстве и ее уравненияСкачать  Вычислим определитель из коэффициентов: Если Δ = 0, кривая второго порядка параболического типа, если Δ > 0, кривая второго порядка эллиптического типа, если Δ F1 и F2 — фокусы.
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.F — фокус параболы, f — директриса параболы. 🔍 ВидеоСеминар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать  §26 Общее уравнение кривых второго порядкаСкачать  Кривые второго порядка. ЗадачиСкачать  13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать  Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать  Семинар 6. Приведение уравнения кривой II порядка к каноническому видуСкачать  |