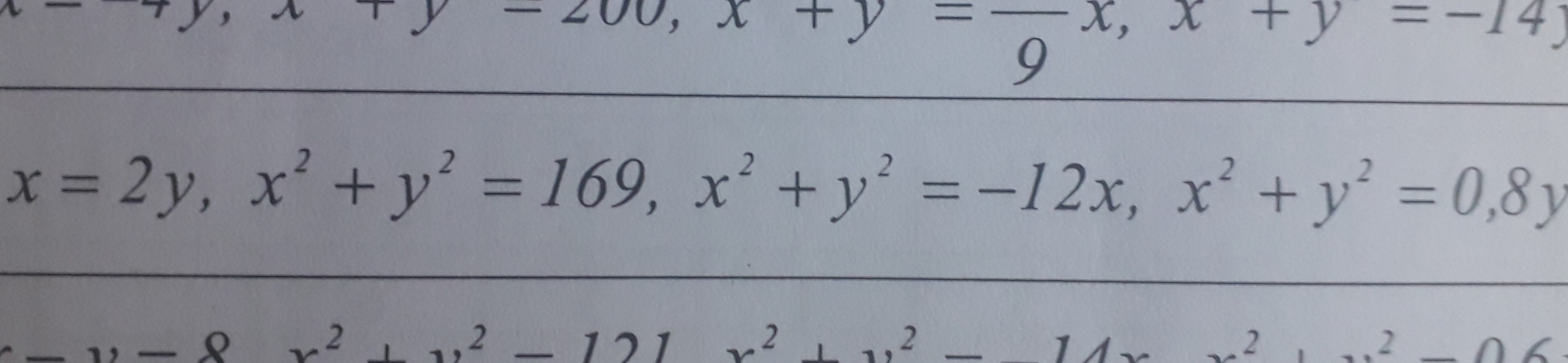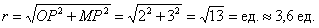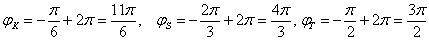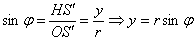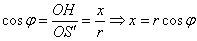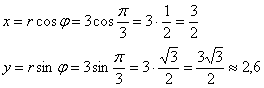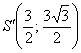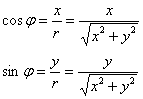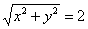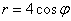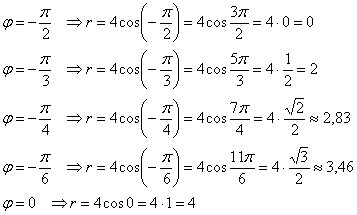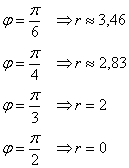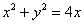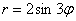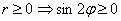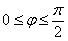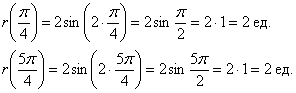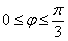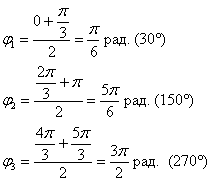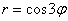Условие
Записать уравнения кривых в полярных координатах и построить их.
Решение
Вводим полярные координаты
x=r*cos φ
y=r*sin φ
1)
x=2y
r*cos φ=2r*sinφ ⇒ tgφ=2 — уравнение линии в полярных координатах
Луч под углом φ к полярной оси, причем tgφ =2
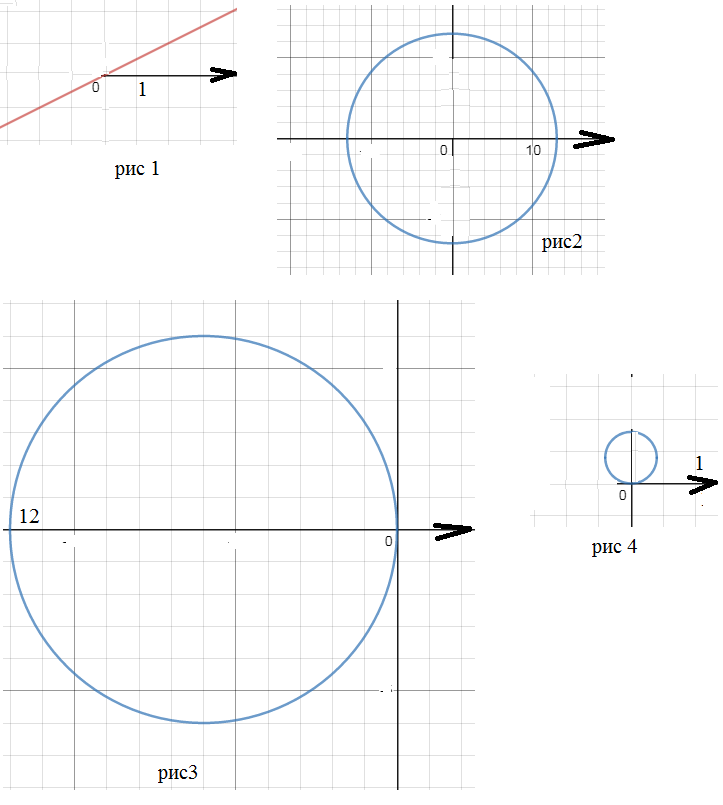
(r*cos φ)^2+(r*sinx φ)^2=169
r^2*(cos^2 φ +sin^2 φ )=13
r=13 — уравнение линии в полярных координатаx
Окружность с центром в точке О радиусом r=13
(r*cos φ)^2+(r*sinx φ)^2=-12*r*cosφ
r^2*(cos^2 φ +sin^2 φ )=-12*r*cosφ
так как r ≥ 0 ⇒ -12cosφ ≥ 0 ⇒ cos φ ≤ 0
Окружность в 2 и 3 четверти
(r*cos φ)^2+(r*sinx φ)^2=0,8*r*sinφ
r^2*(cos^2 φ +sin^2 φ )=0,8*rsinφ
так как r ≥ 0 ⇒ 0,8*sinφ ≥ 0 ⇒ sin φ ≥ 0
Окружность в 1 и 2 четверти
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Полярные координаты
Помимо аффинной системы координат и её популярного частного случая – прямоугольной (декартовой) системы, существуют и другие подходы к построению координатной сетки плоскости и пространства. В частности, широкое распространение получила полярная система координат, которая невероятно удобна для решения целого спектра практических задач. И через считанные минуты, не успевши опомниться, вы уже будете уверенно ориентироваться в полярных координатах!
Чтобы определить полярную систему координат на плоскости, достаточно зафиксировать начало координат 
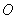
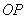
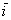
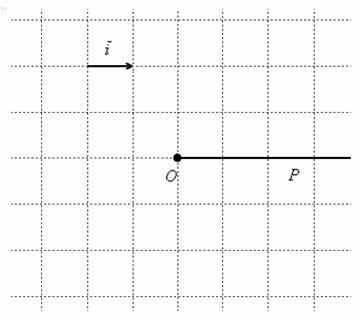
На практике вместо вектора можно где-нибудь в углу указать масштаб, например: 1 ед. = 1 см (две тетрадные клетки). По возможности, старайтесь выбирать именно такую, удобную во многих отношениях метрику.
А теперь сама мякотка:
Любая отличная от начала координат точка 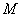
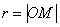
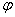
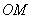
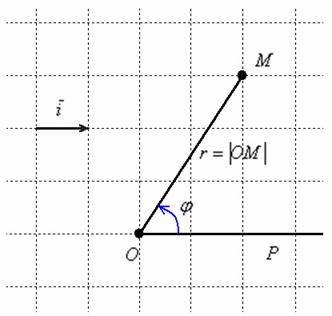
Для самого полюса 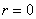
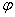
Число 
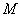
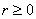
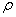
Число 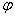
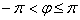
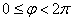
Пару 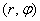
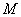
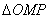
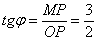
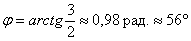
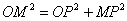
Таким образом, 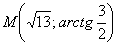
Один пингвин хорошо, а стая – лучше 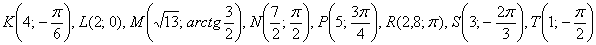
Отрицательно ориентированные углы 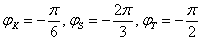
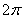
Но недостаток этих «традиционно» ориентированных углов состоит в том, что они слишком далеко (более чем, на 180 градусов) «закручены» против часовой стрелки. Предчувствую вопрос: «почему недостаток и зачем вообще нужны какие-то отрицательные углы?» В математике ценятся самые короткие и рациональные пути. Ну а уж с точки зрения физики направление вращения зачастую имеет принципиальное значение – каждый из нас пытался открыть дверь, дёргая ручку не в ту сторону =)
Порядок и техника построения точек в полярных координатах
Красивые картинки красивы, однако построение в полярной системе координат – занятие достаточно кропотливое. Трудностей не возникает с точками, у которых полярные углы составляют 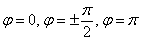
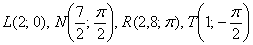
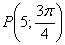
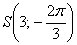
Потребуется клетчатый листок бумаги, карандаш и следующие чертёжные инструменты: линейка, циркуль, транспортир. В крайнем случае, можно обойтись одной линейкой, а то… и вовсе без неё! Читайте дальше и вы получите ещё одно доказательство, что эта страна непобедима =)
Построить точку 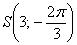
Прежде всего, нужно выяснить градусную меру угла 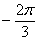
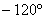
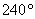
Начертим полярную систему координат (см. начало урока) и возьмём в руки транспортир. Обладателям круглого инструмента не составит труда отметить 240 градусов, но с большой вероятностью у вас на руках будет полукруглая версия девайса. Проблема полного отсутствия транспортира при наличии принтера и ножниц решается рукоделием.
Есть два пути: перевернуть листок и отметить 120 градусов, либо «прикрутить» пол оборота и рассмотреть противоположный угол 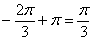
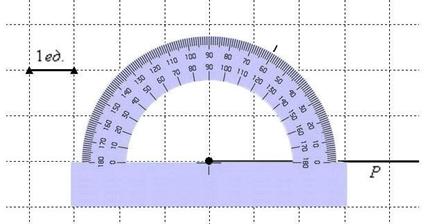
То ли транспортир лилипутский, то ли клетка гигантская =) Впрочем, чтобы отмерить угол масштаб не важен.
Проводим карандашом тонкую прямую, проходящую через полюс и сделанную отметку: 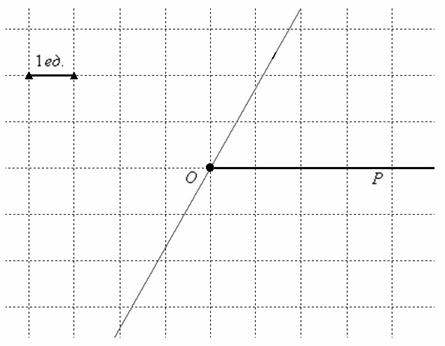
С углом разобрались, на очереди полярный радиус. Берём циркуль и по линейке устанавливаем его раствор в 3 единицы, чаще всего, это, конечно же, сантиметры: 
Теперь аккуратно устанавливаем иглу на полюс, и вращательным движением выполняем небольшую засечку (красный цвет). Искомая точка 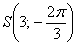
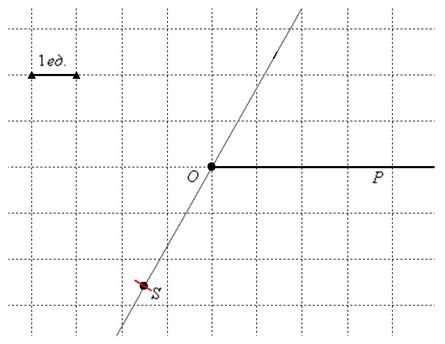
Можно обойтись без циркуля, приложив линейку непосредственно к построенной прямой и отмерив 3 сантиметра. Но, как мы увидим позже, в задачах на построение в полярной системе координат типична ситуация, когда нужно отметить две или бОльшее количество точек с одним и тем же полярным радиусом, поэтому эффективнее закалять металл. В частности, на нашем чертеже, развернув ногу циркуля на 180 градусов, легко сделать вторую засечку и построить симметричную относительно полюса точку 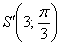
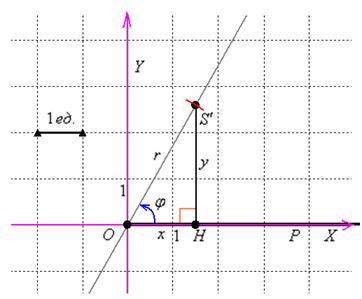
Взаимосвязь прямоугольной и полярной системы координат
Очевидным образом присоединим к полярной системе координат «школьную» систему 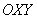
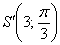
Такое присоединение всегда полезно держать в голове, когда выполняете чертёж в полярных координатах. Хотя, волей-неволей оно напрашивается и без лишнего намёка.
Установим взаимосвязь полярных 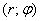
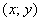
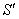
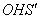
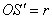
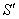
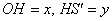
Синус острого угла – есть отношение противолежащего катета к гипотенузе:
Косинус острого угла – есть отношение прилежащего катета к гипотенузе:
Заодно повторили определения синуса, косинуса (и чуть ранее тангенса) из программы 9 класса общеобразовательной школы.
Пожалуйста, занесите в свой справочник рабочие формулы 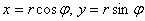
Найдём координаты точки 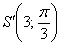
Таким образом:
Полученные формулы открывают ещё одну лазейку в задаче построения, когда можно обойтись вообще без транспортира: сначала находим декартовы координаты точки (понятно, на черновике), затем мысленно находим нужное место на чертеже и отмечаем данную точку. На заключительном этапе проводим тонкую прямую, которая проходит через построенную точку и полюс. В результате получается, что угол якобы был отмерян транспортиром.
Забавно, что совсем отчаянные студенты, могут обойтись даже без линейки, используя вместо неё ровный край учебника, тетради или зачётной книжки – ведь о метрике позаботились производители тетрадей, 1 клетка = 5 миллиметров.
Напомнило мне всё это известный анекдот, в котором находчивые лётчики прокладывали курс по пачке Беломора =) Хотя, шутки шутками, а анекдот не так далёк от реальности, помнится, на одном из внутренних рейсов по РФ в лайнере отказали все навигационные приборы, и экипаж успешно посадил борт при помощи обычного стакана с водой, который показывал угол наклона самолёта относительно земли. А лётная полоса – вот она, из лобового стекла виднА.
Используя процитированную в начале урока теорему Пифагора, легко получить и обратные формулы: 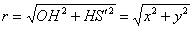
Сам угол «фи» стандартно выражается через арктангенс – абсолютно так же как и аргумент комплексного числа со всеми его заморочками.
Вторую группу формул также целесообразно поместить в свой справочный багаж.
После подробного разбора полётов с отдельно взятыми точками перейдём к закономерному продолжению темы:
Видео:§30 Уравнения кривых второго порядка в полярных координатахСкачать

Уравнение линии в полярных координатах
По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса 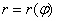
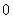
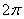
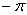
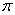
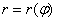
Полярную функцию можно сравнить со своеобразным радаром – когда луч света, исходящий из полюса, вращается против часовой стрелки и «обнаруживает» (прорисовывает) линию.
Дежурным примером полярной кривой является Архимедова спираль 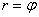
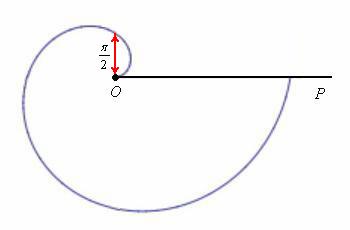
Далее, пересекая полярную ось в точке 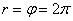
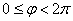
В первом же примере мы сталкиваемся и с понятием области определения полярной функции: поскольку полярный радиус неотрицателен 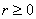
! Примечание: в ряде случаев принято использовать обобщённые полярные координаты, где радиус может быть отрицательным, и такой подход мы вкратце изучим чуть позже
Кроме спирали Архимеда, есть множество других известных кривых, но искусством, как говорится, сыт не будешь, поэтому я подобрал примеры, которые очень часто встречаются в реальных практических заданиях.
Сначала простейшие уравнения и простейшие линии:
Уравнение вида 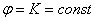
Примечание: в обобщённой полярной системе координат данное уравнение задаёт прямую, проходящую через полюс
Уравнение вида 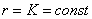
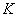
Например, 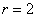
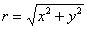
Возведём обе части в квадрат:
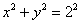
Со времён создания и релиза статьи о линейной зависимости и линейной независимости векторов я получил несколько писем от посетителей сайта, которые задавали вопрос в духе: «вот есть простая и удобная прямоугольная система координат, зачём нужен ещё какой-то косоугольный аффинный случай?». Ответ прост: математика стремится объять всё и вся! Кроме того, в той или иной ситуации немаловажно удобство – как видите, с окружностью значительно выгоднее работать именно в полярных координатах по причине предельной простоты уравнения 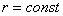
А иногда математическая модель предвосхищает научные открытия. Так, в своё время ректор Казанского университета Н.И. Лобачевский строго доказал, через произвольную точку плоскости можно провести бесконечно много прямых, параллельных данной. В результате он был ошельмован всем научным миром, но… опровергнуть данный факт никто не смог. Только спустя доброе столетие астрономы выяснили, что свет в космосе распространяется по кривым траекториям, где и начинает работать неевклидова геометрия Лобачевского, формально разработанная им задолго до этого открытия. Предполагается, что это свойство самого пространства, кривизна которого нам незаметна ввиду малых (по астрономическим меркам) расстояний.
Рассмотрим более содержательные задачи на построение:
Построить линию
Решение: в первую очередь найдём область определения. Так как полярный радиус неотрицателен, то должно выполняться неравенство 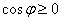
Представьте график косинуса. Если он ещё не успел отложиться в памяти, то найдите его на странице Графики элементарных функций. О чём нам сообщает неравенство 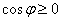
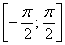
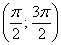
Таким образом, область определения нашей функции: 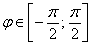
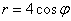
В полярных координатах часто бывает смутное представление о том, какую линию определяет то или иное уравнение, поэтому чтобы её построить, необходимо найти принадлежащие ей точки – и чем больше, тем лучше. Обычно ограничиваются десятком-другим (а то и меньшим количеством). Проще всего, конечно же, взять табличные значения угла. Для бОльшей ясности к отрицательным значениям я буду «прикручивать» один оборот:
В силу чётности косинуса 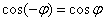
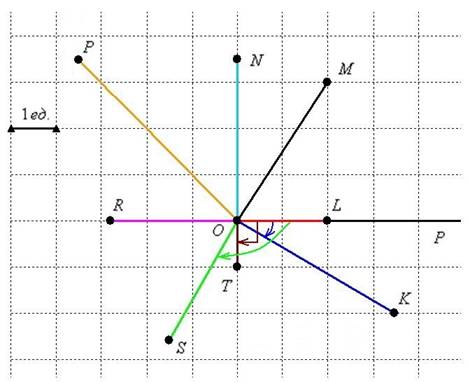
Изобразим полярную систему координат и отложим найденные точки, при этом одинаковые значения «эр» удобно откладывать за один раз, делая парные засечки циркулем по рассмотренной выше технологии: 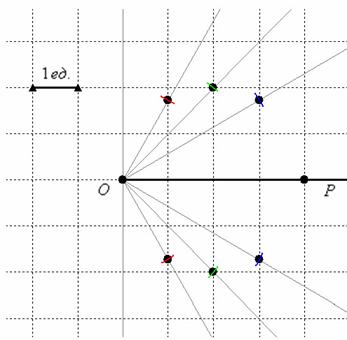
В принципе, линия отчётливо прорисовывается, но чтобы стопроцентно подтвердить догадку, давайте найдём её уравнение в декартовой системе координат. Можно применить недавно выведенные формулы 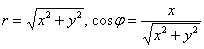
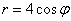
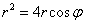
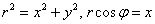
Выделяя полный квадрат, приводим уравнение линии к узнаваемому виду: 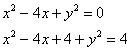
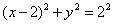
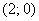
Коль скоро по условию требовалось просто выполнить построение и всё, плавно соединяем найденные точки линией: 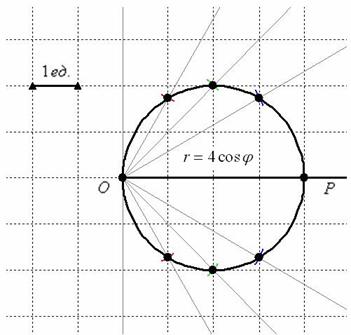
Готово. Ничего страшного, если получится немного неровно, вы же не обязаны были знать, что это окружность 😉
Почему мы не рассмотрели значения угла вне промежутка 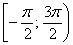
Несложно провести нехитрый анализ и прийти к выводу, что уравнение вида 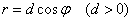
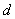
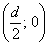
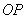
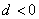
Похожая задача для самостоятельного решения:
Построить линию 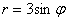
Систематизируем порядок решения задачи:
В первую очередь находим область определения функции, для этого удобно посмотреть на синусоиду, чтобы сразу же понять, где синус неотрицателен.
На втором шаге рассчитываем полярные координаты точек, используя табличные значения углов; проанализируйте, нельзя ли сократить количество вычислений?
На третьем шаге откладываем точки в полярной системе координат и аккуратно соединяем их линией.
И, наконец, находим уравнение линии в декартовой системе координат.
Примерный образец решения в конце урока.
Общий алгоритм и технику построения в полярных координатах мы детализируем
и существенно ускорим во второй части лекции, но перед этим познакомимся ещё с одной распространённой линией:
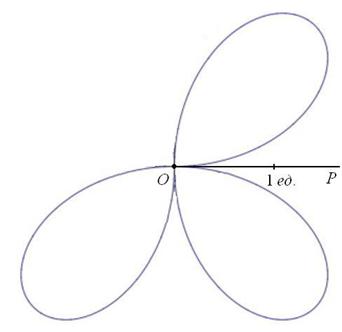
Полярная роза
Совершенно верно, речь пойдёт о цветке с лепестками:
Построить линии, заданные уравнениями в полярных координатах
а) 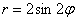
б)
Существует два подхода к построению полярной розы. Сначала пойдём по накатанной колее, считая, что полярный радиус не может быть отрицательным:
Решение:
а) Найдём область определения функции:
Такое тригонометрическое неравенство тоже нетрудно решить графически: из материалов статьи Геометрические преобразования графиков известно, что если аргумент функции удвоить, то её график сожмётся к оси ординат в 2 раза. Пожалуйста, найдите график функции 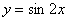
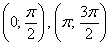
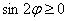
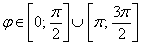
Вообще говоря, решение рассматриваемых неравенств представляет собой объединение бесконечного количества отрезков, но, повторюсь, нас интересует только один период.
Возможно, некоторым читателям более лёгким покажется аналитический способ нахождения области определения, условно назову его «нарезка круглого пирога». Резать будем на равные части и, прежде всего, найдём границы первого куска. Рассуждаем следующим образом: синус неотрицателен, когда его аргумент находится в пределах от 0 до 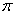
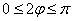
Теперь начинаем последовательно «нарезать равные куски по 90 градусов» против часовой стрелки:
– найденный отрезок 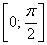
– следующий интервал 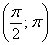
– следующий отрезок 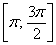
– и, наконец, интервал 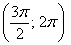
Прямо, как по ромашке – «любит, не любит, любит, не любит» =) С тем отличием, что тут не гадание. Да, прямо какая-то любовь по-китайски получается….
Итак, 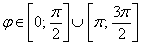
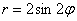
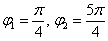
Вот закономерный результат заботливого садовника: 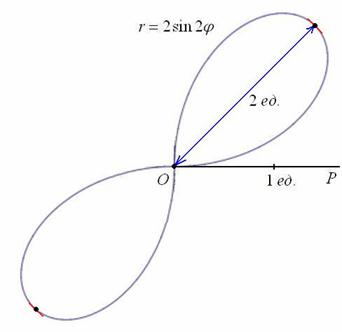
Следует отметить, что длину лепестка легко сразу усмотреть из уравнения 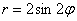
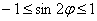
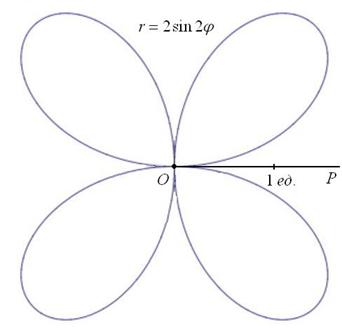
б) Построим линию, заданную уравнением 
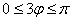
Далее начинаем «нарезку пирога кускам» по 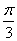
– отрезок 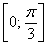
– интервал 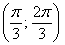
– отрезок 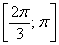
– интервал 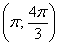
– отрезок 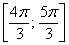
– интервал 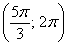
Процесс успешно завершён на отметке 360 градусов.
Таким образом, область определения: 
Проводимые действия полностью либо частично несложно осуществлять и мысленно.
Построение. Если в предыдущем пункте всё благополучно обошлось прямыми углами и углами в 45 градусов, то здесь придётся немного повозиться. Найдём вершины лепестков. Их длина 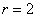
Обратите внимание, что между вершинами лепестков должны обязательно получиться равные промежутки, в данном случае 120 градусов.
Чертёж желательно разметить на 60-градусные секторы (отграничены зелёными линиями) и провести направления вершин лепестков (серые линии). Сами вершины удобно наметить с помощью циркуля – единожды отмерять расстояние в 2 единицы и нанести три засечки на прочерченных направлениях в 30, 150 и 270 градусов: 
Готово. Понимаю, что занятие хлопотное, но если хотите всё оформить по уму, то придётся потратить время.
Сформулируем общую формулу: уравнение вида 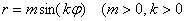
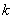
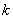
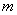
Например, уравнение 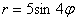
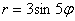
О втором подходе я хотел вообще умолчать, однако не могу пройти мимо – уж слишком он распространён. Суть состоит в том, что полярная роза часто рассматривается в обобщённых полярных координатах, где полярный радиус может быть отрицательным. Вопрос области определения отпадает, но появляются другие приколы.
Во-первых, разберёмся, как строить точки с отрицательным значением «эр». Если 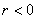
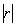
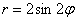
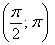
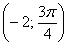
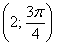
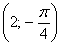
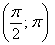
И, соответственно, когда угол проходит значения 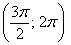
Интересно отметить, что при таком подходе вторая полярная роза 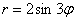
Сформулируем правило розы для обобщенной системы координат: уравнение вида 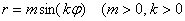
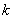
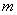
1) если 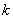
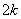
2) если 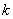
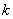
Например, роза 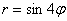
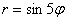
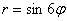
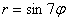
А почему закономерность столь необычна, я только что проиллюстрировал геометрически.
Какой способ выбрать, решать вам, …но я бы не особо рекомендовал использовать обобщенные полярные координаты – у преподавателя могут появиться дополнительные вопросы на счет отрицательных значений полярного радиуса (а то и вообще всё будет забраковано по этой причине)
Короткая задача для самостоятельного решения:
Построить линии, заданные уравнением в полярных координатах
а) 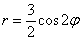
б)
Сформулировать общее правило о количестве и длине лепестков полярной розы вида 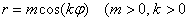
В моём образце решение проведено 1-м способом. Повторим порядок действий:
– Сначала находим область определения. При этом для лучшего понимания своих действий рекомендую соотносить аналитический способ «нарезки» с графической интерпретацией. По материалам урока Геометрические преобразования графиков выясните, как выглядят, и при необходимости начертите графики функций 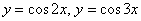
– Находим угловые координаты вершин лепестков – они расположены ровно посередине промежутков области определения.
– Выполняем чертёж. Пойдёт схематическая версия, однако желательно разметить найденные секторы и угловые направления вершин лепестков (в случае необходимости – с помощью транспортира). Вершины удобно засекать циркулем, предварительно установив раствор, равный длине лепестка.
Существуют более солидные и общие формулы окружности, полярной розы и желающие могут с ними ознакомиться в других источниках информации. Я лишь ограничился практически значимыми (с моей точки зрения) примерами.
Предлагаю перейти ко 2-й части занятия под названием Как построить линию в полярной системе координат?, где мы продолжим рассматривать типовые задачи, и усовершенствуем свои навыки.
Решения и ответы:
Пример 3: Решение: найдём область определения: 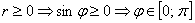
Вычислим полярные координаты точек, принадлежащих данной линии: 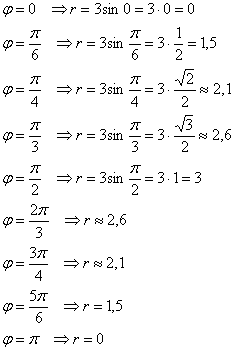
Выполним чертёж: 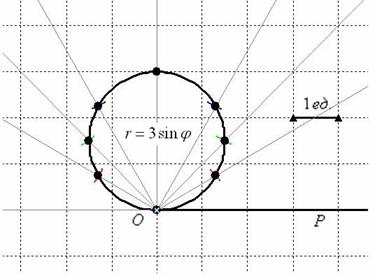
Найдём уравнение линии в декартовой системе координат: 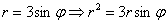
Проведём замены 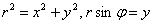
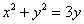
Выделим полный квадрат: 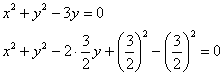
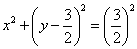
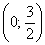
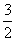
Дополнительная информация: уравнение вида 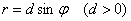
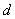
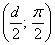
Пример 5: Решение:
а) Найдём область определения: косинус неотрицателен, когда его аргумент находится в пределах от 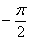
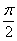
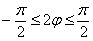
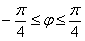
Таким образом:
– отрезок 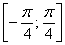
– интервал 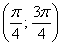
– отрезок 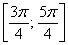
– интервал 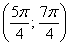
Область определения: 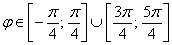
Роза имеет два лепестка, вершины которых находятся на полярной оси и её продолжении, длина лепестка равна 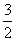
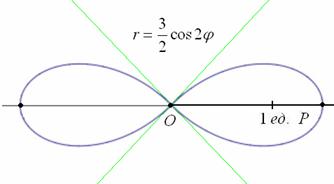
б) область определения: 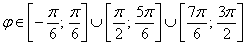
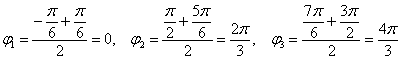
Выполним чертёж: 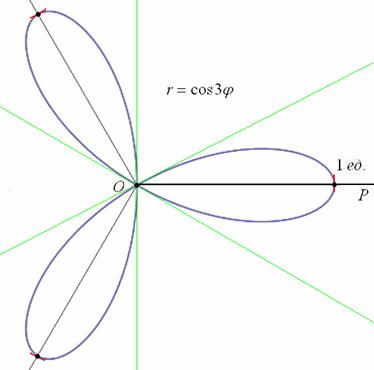
Уравнение вида 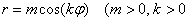
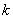
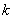
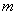
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Видео:Построение кривой в полярной системе координатСкачать

Полярное уравнение кривой второго порядка.
Пользуясь общим свойством эллипсов, гипербол и парабол, выведем общее уравнение этих кривых второго порядка в полярных координатах при некотором специальном выборе полярной системы координат.
Пусть дана произвольная из указанных линий (эллипс, ветвь гиперболы или парабола). Возьмем фокус F кривой (любой, если их два) и соответствующую ему директрису L (если рассматривается ветвь гиперболы, то берется фокус и директриса, ближайшие к этой ветви).
Введем полярную систему координат так, чтобы полюс О совпал с фокусом F, а полярная ось была направлена по оси симметрии кривой в сторону, противоположную директрисе L.
Возьмем на кривой произвольную точку М(r;j), соединим ее отрезком FM с фокусом и опустим перпендикуляр МК на директрису. Кроме того, из точки F проведем перпендикуляр FR к полярной оси до пересечения с кривой в точке R, а из точки R опустим перпендикуляр RQ на директрису (Рис. 12).
 | Обозначим FR через p и будем называть это число фокальным параметром. На основании общего свойства кривых второго порядка  По тем же соображениям: По тем же соображениям:  или или  , откуда , откуда  . . |
Подставим найденные выражения для FM и КМ в равенство 

Уравнение (3) называется уравнением кривой второго порядка в полярных координатах. При e 1 — ветвью гипиерболы, при e=1 — параболой.
Фокальный параметр Р из уравнения параболы определяется непосредственно. Для того, чтобы фокальный параметр выразить через параметры эллипса и гиперболы, следует заметить, что фокальный параметр Р является ординатой точки кривой, абсцисса которой равна абсциссе соответствующего фокуса (в выбранной при выведении канонического уравнения соответствующей кривой системе ХОY).
Подставляя вместо координат точки М(х;у) в уравнение эллипса 



Аналогично, подставляя в уравнение гиперболы координаты точки (с;р), получим:


откуда следует соотношение

Рассмотрим несколько задач на кривые второго порядка.
Задача 1.
Дано уравнение гиперболы 16х 2 -9у 2 =144. Найти длины ее осей, координаты фокусов, эксцентриситет; составить уравнения директрис и асимптот гиперболы.
Решение.
Приведем уравнение гиперболы к каноническому виду и определим как параметры гиперболы, так и расстояние с от начала координат до фокуса:


откуда а=3, b=4, 

Действительная ось 2а=6; мнимая ось 2b=8.
Уравнения директрис: 
Уравнения асимптот: 
Задача 2.
Составить уравнение эллипса, симметричного относительно координатных осей, зная, что он проходит через точки М1(2;3) и М2 
Решение.
Учитывая симметричность эллипса относительно осей координат, его каноническое уравнение будет иметь вид: 
определим параметры эллипса а и b.


получим следующую систему уравнений:

Решая ее, получим, что:

откуда а 2 =16, b 2 =12.
Следовательно, искомое уравнение эллипса будет:

Задача 3.
Найти вершину, фокус, ось и директрису параболы
Решение.
Преобразуем данное уравнение следующим образом:
Отсюда 
Обозначив х`= х-4 и у`= у-3, перейдем к новой системе координат O`x`y`, начало которой находится в точке O`(4;3), а оси O`x` и O`y` сонаправлены с осями Ох и Оу. В результате получим простейшее уравнение данной параболы

Отсюда 

xF = xO` = 4; 
то есть F 

Задача 4.
Уравнение эллипса 

Решение:
Найдем из данного уравнения параметры a, b, c, затем найдем эксцентриситет 

а 2 =4, b 2 =3, c 2 =1, 

Искомое уравнение будет иметь вид:



Задача 5.
Дано уравнение кривой в полярных координатах

Привести его к каноническому уравнению в прямоугольных координатах.
Решение.
В данном уравнении 

Из этой системы находим, что а=1, с=3, b 2 =8. Следовательно, уравнение гиперболы имеет вид:

🎬 Видео
Глаза гипножабы и площадь фигур в полярной системе координатСкачать

Полярная система координатСкачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Полярная система координатСкачать

Видеоурок "Полярная система координат"Скачать

Оператор Лапласа в полярных координатахСкачать

Скорость и ускорение точки в полярных координатахСкачать

Полярные координаты. Полярное уравнение эллипса.Скачать

Полярная система координат.Скачать

Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Площадь фигуры, заданной в полярной системе координатСкачать

Занятие 01. Часть 3. Полярная система координатСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Площади 12Скачать

§12 Полярное уравнение прямойСкачать

Построение графика функции в полярных координатахСкачать

Найти производную y'(x), если кривая задана в полярных координатахСкачать