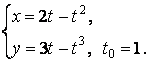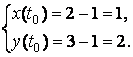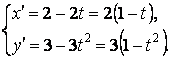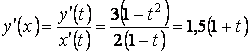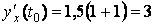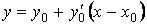Составить уравнение касательной и нормали к данным линиям в указанных точках x 2e t

&nbsp &nbsp &nbsp &nbsp Вариант 1 &nbsp &nbsp Вариант 2 &nbsp &nbsp Вариант 3 &nbsp &nbsp Вариант 4 &nbsp &nbsp Вариант 5 &nbsp &nbsp Вариант 6

&nbsp &nbsp &nbsp &nbsp Вариант 7 &nbsp &nbsp Вариант 8 &nbsp &nbsp Вариант 9 &nbsp &nbsp Вариант 10 &nbsp &nbsp Вариант 11 &nbsp &nbsp Вариант 12

&nbsp &nbsp Вариант 13 &nbsp &nbsp Вариант 14 &nbsp &nbsp Вариант 15 &nbsp &nbsp Вариант 16 &nbsp &nbsp Вариант 17 &nbsp &nbsp Вариант 18

&nbsp &nbsp Вариант 19 &nbsp &nbsp Вариант 20 &nbsp &nbsp Вариант 21 &nbsp &nbsp Вариант 22 &nbsp &nbsp Вариант 23 &nbsp &nbsp Вариант 24

&nbsp &nbsp Вариант 25 &nbsp &nbsp Вариант 26 &nbsp &nbsp Вариант 27 &nbsp &nbsp Вариант 28 &nbsp &nbsp Вариант 29 &nbsp &nbsp Вариант 30

&nbsp &nbsp &nbsp &nbsp 16.4. Составить уравнение касательной и нормали к кривой в точке, соответствующей значению параметра t=t0.

Решение.

&nbsp &nbsp &nbsp &nbsp Найдём координаты точки:

&nbsp &nbsp &nbsp &nbsp Найдём производные:

&nbsp &nbsp &nbsp &nbsp Тогда производная функции, заданной параметрически:

&nbsp &nbsp &nbsp &nbsp В точке &nbsp &nbsp &nbsp &nbsp имеем

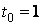
&nbsp &nbsp &nbsp &nbsp Уравнение касательной

&nbsp &nbsp &nbsp &nbsp Уравнение нормали

&nbsp &nbsp &nbsp &nbsp Для нашего случая получаем: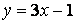

&nbsp &nbsp &nbsp &nbsp — уравнение касательной;

&nbsp &nbsp &nbsp &nbsp — уравнение нормали.

&nbsp &nbsp &nbsp &nbsp — уравнение нормали.

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end

Пусть в точке $M$ $ vec(t_0)neqvec$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.

Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).

Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:

Уравнение в каноническом виде распишите самостоятельно.

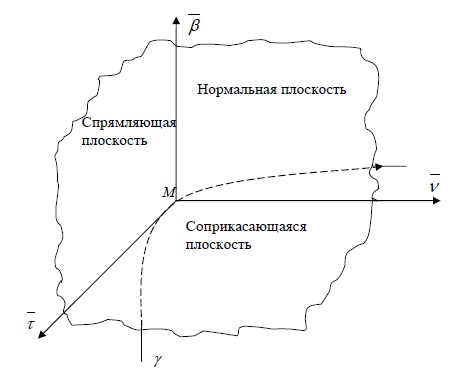
Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ vec=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$

Правая тройка векторов $vec$, $vec$, $vec$ называется репером Френе.

Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Решение задач

Задача 1

Кривая $gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end

begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end

begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec$, $vec$, $vec$ не будет правой (по определению векторного произведения вектор $vectimesvec$ направлен так, что тройка векторов $vec$, $vec$, $vec=vectimesvec$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $vec$, $vec$, $vec<tilde>$ образует репер Френе для кривой $gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac,,, z=frac, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end

begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.

Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_=2,, t_=-frac25. end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end

Видео:Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Уравнение касательной и уравнение нормали к графику функции

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Как получить уравнение касательной и уравнение нормали

Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.

Уравнение касательной выводится из уравнения прямой.

Выведем уравнение касательной, а затем — уравнение нормали к графику функции.

В нём k — угловой коэффициент.

Отсюда получаем следующую запись:

Значение производной f ‘(x 0 ) функции y = f(x) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f(x 0 ) . В этом состоит геометрический смысл производной.

Таким образом, можем заменить k на f ‘(x 0 ) и получить следующее уравнение касательной к графику функции:

В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали:

Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне).

Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».

Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .

Видео:Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать

Решаем задачи вместе

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции (функция представляет собой многочлен и её производную можно найти по формулам 1, 2 и 3 в таблице производных):

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.

Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:

Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

Составляем уравнение нормали:

Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Находим уравнение касательной:

Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

Составляем уравнение нормали:

Видео:3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

Решить задачи самостоятельно, а затем посмотреть решения

Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Видео:Уравнение касательнойСкачать

Снова решаем задачи вместе

Пример 6. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).

Пример 7. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Внимание! Данная функция — сложная, так как аргумент тангенса ( 2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции (потребуется формула 9 в таблице производных сложной функции):

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Пример 8. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Как и в предыдущем примере, данная функция — сложная, так как степень () сама является функцией. Поэтому найдём производную функции как производную сложной функции (используя формулу 1 в таблице производных сложной функции):

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

🎦 Видео

Как составить уравнение касательной и нормали к графику функцииСкачать

Уравнения касательной и нормали к кривойСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

14.1. Касательная к параметрически заданной функцииСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

УРАВНЕНИЕ КАСАТЕЛЬНОЙ И НОРМАЛИ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение касательнойСкачать

Касательная к графику функции в точке. 10 класс.Скачать

11.1. Касательная к неявной функции / производная неявной функции ПРИМЕРЫСкачать

Уравнения касательной и нормали к графику функции (часть 1). Высшая математика.Скачать