Условие
5) Найти уравнение гиперболы, зная, что ее эксцентриситет ε = 2, фокусы гиперболы совпадают с фокусом эллипса x^2/10 + y^2 = 1.
Решение
Каноническое уравнение эллипса
(x^2/10) + y^2 = 1
a=sqrt(10)
b=1
b^2=a^2-c^2 ⇒ c^2=a^2-b^2=10-1=9
Фокусы эллипса
F_(1)(-3;0) и F_(2)=(3;0)
Фокусы гиперболы
F_(1)(-3;0) и F_(2)=(3;0)
эксцентриситет гиперболы ε=с/a ⇒
2=3/a ⇒ a=3/2
b^2=c^2-a^2=3^2-(3/2)^2=9-(9/4)=27/4
О т в е т. (x^2/(3/2)^2)-(y^2/(3sqrt(3)/2)^2)=1
или
108x^2-36y^2=243
Видео:Видеоурок "Гипербола"Скачать

Составить уравнение гиперболы с фокусами эллипса
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, равная 2 a .
Обозначим фокусы через F 1 и F 2 , расстояние между ними через 2 c , а сумму расстояний от произвольной точки эллипса до фокусов – через 2 a . По определению 2 a > 2 c , то есть a > c .
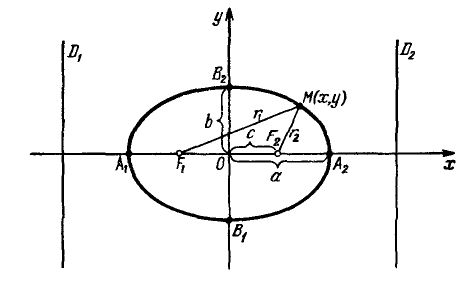
Выберем систему координат так, чтобы фокусы F 1 и F 2 лежали на оси 0 x , а начало координат совпадало с серединой отрезка F 1 F 2 . Тогда фокусы имют координаты: F 1 (– c ;0) и F 2 ( c ;0) . Пусть M ( x ; y ) – произвольная точка эллипса (текущая точка). Тогда по определению эллипса можно записать
По сути, мы получили уравнение эллипса. Упростим его с помощью ряда несложных математических преобразований:
Это уравнение равносильно первоначальному. Оно называется каноническим уравнением эллипса – кривой второго порядка .
Установим форму эллипса, пользуясь его каноническим уравнением.
1. Уравнение (2.17) содержит x и y только в четных степенях, поэтому если точка ( x ; y ) принадлежит эллипсу, то ему также принадлежат точки (– x ; y ), ( x ;– y ), (– x ;– y ) . Отсюда: эллипс симметричен относительно осей 0 x и 0 y , а также относительно точки O (0;0), которую называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат. Положив y = 0, найдем точки A 1 ( a ; 0) и A 2 (– a ; 0), в которых ось 0 x пересекает эллипс. Положив в уравнении (2.17) x = 0, находим точки пересечения эллипса с осью 0 y : B 1 (0; b ) и B 2 (0;– b ). Точки A 1 , A 2 , B 1 , B 2 называются вершинами эллипса. Отрезки А1А2, В1В2, а также их длины 2 a и 2 b – соответственно большая и малая оси эллипса (рис. 2.4).
3. Из уравнения (2.17) следует, что каждое слагаемое в левой части не превосходит единицы, т.е.:
Следовательно, все точки эллипса лежат внутри прямоугольника, ограниченного прямыми x = ± a и y = ± b .
4. В уравнении (2.17) левая часть – сумма неотрицательных слагаемых, т.е. при возрастании одного слагаемого другое будет уменьшаться, если | x | возрастает, | y | уменьшается и наоборот.
Из сказанного следует, что эллипс имеет форму овальной замкнутой кривой. Форма эллипса зависит от отношения 


Отсюда видно, что чем меньше эксцентриситет эллипса, тем будет менее эллипс сплющенным; при ε = 0 эллипс превращается в окружность.
Прямые 
Если r – расстояние от произвольной точки до какого–нибудь фокуса, d – расстояние от этой же точки до соответствующей этому фокусу директрисы (рис. 2.5), то отношение 

Из равенства a 2 – c 2 = b 2 следует, что a > b . Если же наоборот, то уравнение (2.17) определяет эллипс, большая ось которого 2 b лежит на оси 0 y , а малая ось 2 a – на оси 0 x . Фокусы такого эллипса находятся в точках F 1 (0; c ) и F 2 (0;– c ) , где 
Пример 2.5. Составить уравнение линии, для каждой точки которой отношение расстояний от нее до точки A (3;0) и до прямой x = 12, равно числу ε =0,5 . Полученное уравнение привести к простейшему виду .
Решение . Пусть M ( x ; y ) – текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр MB на прямую . Тогда точка B( 12;y) . По условию задачи 
По формуле расстояния 
Эксцентриситет эллипса
Примечание. Если эллипс (окружность) вращать вокруг одной из его осей, то описываемая им поверхность будет эллипсоидом вращения (сферой) 
Пример 2.6. В геодезии используется система географических координат, основанная на понятии геоида. Геоид – поверхность Земли, ограниченная уровенной поверхностью, продолженной под континенты. Поверхность геоида отличается от физической поверхности Земли, на которой резко выражены горы и океанические впадины.
Тело, поверхность которого более всего соответствует поверхности геоида, имеет определенные размеры и ориентирована соответственно в теле Земли, называется референц–эллипсоидом. В нашей стране с 1946 года для всех геодезических работ принят референц–эллипсоид Красовского с параметрами a = 6 378 245 м, b = 6 356 863 м, α = 1: 298,3.
Линия, проходящая вертикально через центр эллипсоида является полярной осью. Линия, проходящая через центр эллипсоида, перпендикулярно к полярной оси, – экваториальной осью. При пересечении поверхности эллипсоида плоскостью, проходящей через его центр, перпендикулярно к полярной оси, образуется окружность, называемая экватором. Окружность, полученная от пересечения поверхности эллипсоида плоскостью, параллельной плоскости экватора, называется параллелью. Линия пересечения поверхности эллипсоида с плоскостью, проходящей через заданную точку и полярную ось, называется меридианом данной точки. Положение точки на земной поверхности определяется пересечением параллели и меридиана, проходящих через нее. Угол φ между плоскостью экватора и отвесной линией называется географической широтой. Для определения долгот точек один из меридианов (Гринвичский) принимают за начальный или нулевой. Угол λ, составленный плоскостью меридиана, проходящего через данную точку, и плоскостью начального меридиана, называется географической долготой
Гипербола – геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости – фокусов, есть величина постоянная, равная 2 a .
Обозначим фокусы через F 1 и F 2 , расстояние между ними через 2 c , а модуль разности расстояний от каждой точки гиперболы до фокусов через 2 a . По определению 2 a 2 c , то есть a c .
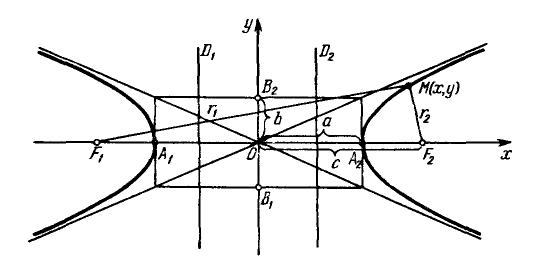
Выберем систему координат x 0 y так, чтобы фокусы F 1 и F 2 лежали на оси 0 x , а начало координат совпало с серединой отрезка F 1 F 2 . Тогда фокусы будут иметь координаты F 1( c ;0 ) и F 2 (– c ;0 ). На этой основе выведем уравнение гиперболы. Пусть M ( x ; y ) – ее произвольная точка . Тогда по определению | MF 1 – MF 2 |= 2 a , то есть 
где b 2 = a 2 – c 2 . Гипербола – линия 2–го порядка.
Установим форму гиперболы, исходя из ее канонического уравнения.
1. Уравнение (2.18) содержит x и y только в четных степенях. Следовательно, гипербола симметрична относительно осей координат 0 x и 0 y , и относительно точки O (0;0) – центра гиперболы.
2. Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (2.18) y =0 , находим две точки пересечения гиперболы с осью 0 x : A 1 ( a ; 0) и A 2 (– a ; 0).
Положив в (2.18) x = 0, получаем y 2 = – b 2 , чего быть не может. Т.е. гипербола ось 0 y не пересекает.
3. Из уравнения (2.18) следует, что уменьшаемое 
4. Из уравнения (2.18) гиперболы видно, что когда | x | возрастает, то | y | также возрастает . Это следует из того, что разность 
Прямая L называется асимптотой некоторой неограниченной кривой , если расстояние d от точки M этой кривой до прямой L стремится к нулю при неограниченном удалении т очки M вдоль кривой от начала координат.
Покажем, что гипербола 

Возьмем на прямой 

Очевидно: так как числитель есть величина постоянная, а знаменатель дроби увеличивается с возравстанием переменной х, то длина отрезка | MN | стремится к нулю. Так как | MN | больше расстояния d от точки M до прямой L, то d стремится к нулю тем более ( и подавно) . Следовательно, прямые 
Построение гиперболы начинают с нанесения ее основного прямоугольника на координатную плоскость. Далее проводят диагонали этого прямоугольника, которые являются асимптотами гиперболы, затем отмечают ее вершины, фокусы и строят ветви гиперболы .
Эксцентриситет гиперболы – отношение расстояния между фокусами к величине её действительной оси, обозначается ε : 


Эксцентриситет равносторонней гиперболы равен 

Прямые 


Уравнение 
Значит , гиперболы 
Примечание. Если у кривой 2–го порядка смещен центр в некоторую точку O ’ ( x 0 ; y 0 ) , то она называется нецентральной кривой. Уравнение такой кривой имеет вид:
Примечание. При вращении гиперболы вокруг ее действительной оси образуется двуполостный гиперболоид, вокруг ее мнимой оси – однополостный гиперболоид
Подробно данные уравнения рассмотрены в теме: «Исследование общего уравнения 2–ой степени» (смотри схему 10), частными случаями которого являются данные формулы.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Математический портал
Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Nav view search
Navigation
Search
- Вы здесь:
- Home
- Аналитическая геометрия
- Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.
Видео:Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Эллипс.
Эллипс с каноническим уравнением $frac+frac=1, ageq b>0,$ и меет форму изображенную на рисунке.
Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ — главными осями а центр симметрии $O -$ центром эллипса.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами эллипса векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $frac+frac=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.
Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.
Теорема. ( Директориальное свойство эллипса)
Эллипс является множеством точек, отноше ние расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$
Примеры.
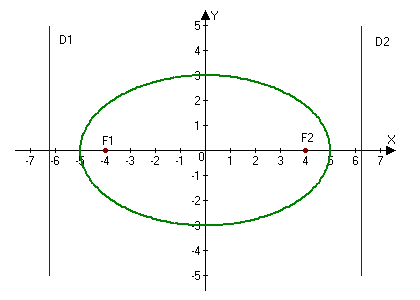
2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.
Приведем уравнение эллипса к каноническому виду:
а) Находим полуоси $a=5,$ $b=3.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$
$c=sqrt=sqrt=4Rightarrow F_1(-4, 0),qquad F_2(4, 0).$
г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),qquad F_2(4, 0);$ в) $e=frac;$ г) $D_1: x=-frac$ и $D_2: x=frac.$
2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.
Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:
Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=sqrt 5.$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac=-frac $ и $D_2: x=frac=frac.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=sqrt 5;$ $ e=frac.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$
2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.
Решение.
Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$
Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, sqrt 3)$ в каноническое уравнение эллипса $frac+frac=1:$
Таким образом, уравнение эллипса $frac+frac=1.$
Далее найдем координаты фокусов:
$c=sqrt=sqrt=2sqrt 3Rightarrow F_1(-2sqrt 3, 0),,,, F_2(2sqrt 3, 0).$
Отсюда находим $overline =(2+2sqrt 3, sqrt 3),$ $overline=(2-2sqrt 3, sqrt 3).$
Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$
Таким образом, расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_1: sqrt 3 x+8=0$
расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_2: sqrt 3 x-8=0$
Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) — $ ее вершинами. Оси симметрии $Ox$ и $Oy$ — действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами гиперболы, векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.
Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.
Теорема. (Директориальное свойство гиперболы).
Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей дирек трисы постоянно и равно $e.$
Примеры.
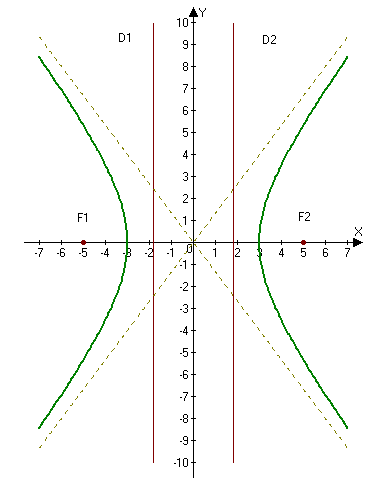
2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.
Приведем уравнение гиперболы к каноническому виду:
а) Находим полуоси $a=3,$ $b=4.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$
$c=sqrt=sqrt=5Rightarrow F_1(-5, 0),qquad F_2(5, 0).$
г) Асимптоты гиперболы находим по формулам $y=pmfracx:$
д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),qquad F_2(5, 0);$ в) $e=frac;$ г) $y=pmfracx;$ д ) $D_1: x=-frac$ и $D_2: x=frac.$
2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.
Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:
Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$
Асимптоты гиперболы c центром в начале координат, находим по формулам $y=pmfracx,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=pmfrac(x-x_0),$
$$y+3=frac(x-2)Rightarrow 3y+9=4x-8Rightarrow 4x-3y-17=0.$$
$$y+3=-frac(x-2)Rightarrow 3y+9=-4x+8Rightarrow 4x+3y+1=0.$$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac=-frac $ и $D_2: x=frac=frac.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=frac,$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$
2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $frac-frac=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.
Решение.
Проверим, что заданная точка лежит на гиперболе:
Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $frac-frac=1.$
Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:
$c=sqrtRightarrow c=sqrt=sqrt =5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$
Фокальные радиусы точки, можно найти по формулам $r_1=|overline|$ и $r_2=|overline|.$
Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-fracRightarrow x=-fracRightarrow 5x+16=0;$
$D_2: x=fracRightarrow x=fracRightarrow 5x-16=0;$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$
Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: sqrt 5x+16=0$
расстояние от точки $M(5, 9/4)$ до прямой $D_2: sqrt 5x-16=0$
Ответ: $r_1=9/4,$ $r_2=frac;$ $d_1=frac;$ $d_2=frac.$
2.273. Найти точки гиперболы $frac-frac=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$
Решение.
Из уравнения гиперболы находим полуоси: $a=3, , b=4.$ Следовательно, $c=sqrtRightarrow c=sqrt=sqrt =5.$
Отсюда находим $F_1=(-5, 0).$
Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$
Чтобы н айти точки гиперболы $frac-frac=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений
Решим уравнение $5x^2+18x-72=0:$
Находим соответствующие координаты $y:$ $y_1=pmsqrt=sqrt$ — нет корней .
Ответ: $(-6, pm4sqrt 3).$
Парабола.
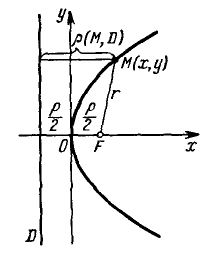
Парабола с каноническим уравнением $y^2=2px, p>0,$ и меет форму изображенную на рисунке.
Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ — осью параболы.
Точка $Fleft(frac
, 0right)$ называется фокусом параболы, вектор $overline -$ фокальным радиус-векторам, а число $r=|overline| -$ фокальным радиусом точки $M,$ принадлежащей параболе.
Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.
Примеры.
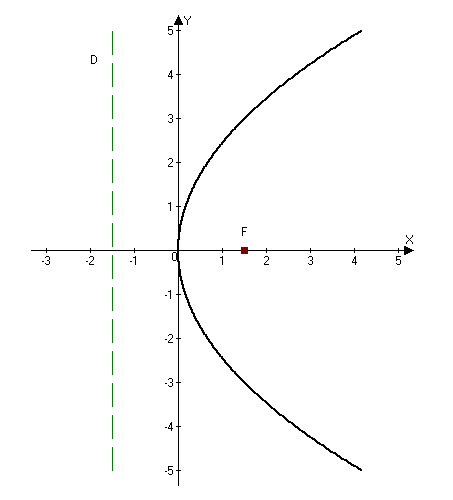
2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.
Решение.
Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $
$$y^2=6xRightarrow y^2=2cdot 3xRightarrow p=2.$$
Ответ: $p=3.$
2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$
Решение.
Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:
Ответ: $y^2=-x.$
2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$
Решение.
Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$
Приведем заданное уравнние к такому виду:
Таким образом, $y^2=4(x^2-2)$ — парабола с центром в точке $(0, 2).$ Параметр $p=2.$
Ответ: $C(0, 2),$ $p=2.$
2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$
Решение.
Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12xRightarrow 36=12xRightarrow x=3.$$
Таким образом, точка $M$ имеет координаты $(3, 6).$
Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2cdot 6xRightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$
Далее находим фокальный параметр точки:
Ответ: $6.$
2.298. Из фокуса параболы $y^2=12x$ под острым углом $alpha$ к оси $Ox$ направлен луч света, причем $tgalpha=frac.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.
Решение.
Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2cdot 6xRightarrow p=6.$
Координаты фокуса $F(p/2, 0)Rightarrow F(3,0).$
Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $alpha: tgalpha=frac$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tgalpha=frac.$
Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$
$0=fraccdot 3+bRightarrow b=-frac.$ Таким образом, уравнение луча, направленного из фокуса $y=fracx-frac.$
Далее, найдем точку пересечения найденной прямой с параболой:
Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=frac=frac=27.$
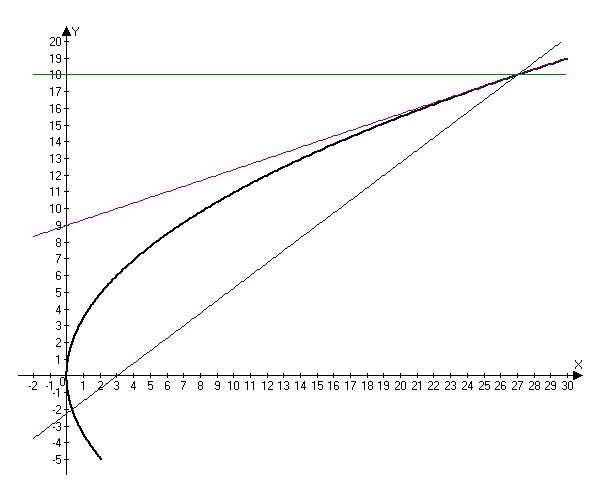
Таким образом, луч пересекает параболу в точке $(27, 18).$
Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$
Подставляем все найденные значения в уравнение касательной:
$y-18=frac(x-27)Rightarrow 3y-54=x-27Rightarrow x-3y+27=0.$
Далее, найдем угол $beta$ между лучем $y=fracx-frac$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=frac$
$$L_2: x-3y+27=0Rightarrow y=fracx+9Rightarrow k_2=frac.$$
Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $pi-2beta,$ а угол между отраженным лучем и осью $Ox$ $pi-(pi-2beta)-alpha=2beta-alpha.$
Зная $tgbeta=frac$ и $tgalpha=k_1=frac$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2beta-alpha):$
$$tg(2beta-alpha)=frac=frac<frac-frac><1+fracfrac>=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$
📽️ Видео
Фокусы эллипсаСкачать

Фокусы гиперболыСкачать

§29 Эксцентриситет гиперболыСкачать

165. Найти фокусы и эксцентриситет эллипса.Скачать

Уравнение эллипса. Нахождение вершин и фокусовСкачать

Неполное уравнение второго порядка. Эллипс, гипербола. ЗадачиСкачать

§28 Эксцентриситет эллипсаСкачать

Лекция 14, 2021. Вывод уравнения эллипса и гиперболыСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

ЭллипсСкачать

Видеоурок "Эллипс"Скачать

Эллипс. Гипербола. Их вырожденияСкачать

§21 Каноническое уравнение гиперболыСкачать

Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

11 класс, 52 урок, ЭллипсСкачать

§22 Исследование канонического уравнения гиперболыСкачать