Составить уравнение гиперболы проходящей через точку а 9 4 если а 3 (4 видео)

Составить уравнение гиперболы проходящей через точку а 9 4 если а 3

Гипербола проходит через точки и . Найти уравнение гиперболы.

может быть записано так

Определению подлежат a 2 и b 2 . Подставим в это уравнение координаты первой точки и получим

Подставляя в уравнение гиперболы (1) координаты второй точки, получим

Решим систему уравнений

Умножая первое уравнение на 4, а второе на 3 и вычитая из второго первого, получим a 2 = 5. Подставим a 2 = 5 в первое уравнение и получим 20b 2 — 45 = 5b 2 , откуда b 2 = 3. Подставляя найденные значения a 2 и b 2 в (1), получим, что искомое уравнение имеет вид

Содержание

Задача 62181 Уравнение гиперболы, 19 задание под.
Условие
Решение
Гипербола: формулы, примеры решения задач
Определение гиперболы, решаем задачи вместе
Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
🔥 Видео

Видео:Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Задача 62181 Уравнение гиперболы, 19 задание под.

Условие

Уравнение гиперболы, 19 задание под б)Составить уравнение гиперболы , если она проходит через точку А(9;32) и уравнение ее асимптот у=+-корень из 3/3 *х

Решение

Каноническое уравнение гиперболы с действительной осью х:

Тогда уравнение асимптот этой гиперболы

Уравнение гиперболы можно записать в виде:

Чтобы найти a подставляем координаты точки A(9;32)

[m]a^2

Видео:Видеоурок "Гипербола"Скачать

Гипербола: формулы, примеры решения задач

Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Определение гиперболы, решаем задачи вместе

Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы имеет вид:

где a и b — длины полуосей, действительной и мнимой.

На чертеже ниже фокусы обозначены как и .

На чертеже ветви гиперболы — бордового цвета.

При a = b гипербола называется равносторонней.

Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.

Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.

Точки и , где

называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).

называется эксцентриситетом гиперболы.

Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.

Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.

Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,

Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.

То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.

Подставляем и вычисляем:

Получаем требуемое в условии задачи каноническое уравнение гиперболы:

Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет .

Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет — это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:

Результат — каноническое уравнение гиперболы:

Если — произвольная точка левой ветви гиперболы () и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

Если — произвольная точка правой ветви гиперболы () и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

На чертеже расстояния обозначены оранжевыми линиями.

Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.

Прямые, определяемые уравнениями

называются директрисами гиперболы (на чертеже — прямые ярко-красного цвета).

Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

где — расстояние от левого фокуса до точки любой ветви гиперболы, — расстояние от правого фокуса до точки любой ветви гиперболы и и — расстояния этой точки до директрис и .

Пример 4. Дана гипербола . Составить уравнение её директрис.

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. . Вычисляем:

Получаем уравнение директрис гиперболы:

Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.

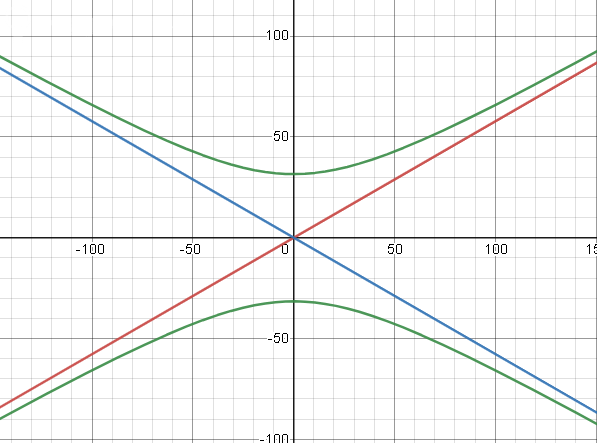
Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.

Асимптоты гиперболы определяются уравнениями

На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.

Уравнение гиперболы, отнесённой к асимптотам, имеет вид:

, где .

В том случае, когда угол между асимптотами — прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.

Пример 5. Даны уравнения асимптот гиперболы и координаты точки , лежащей на гиперболе. Составить уравнение гиперболы.

Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения . Для этого подставляем в формулу канонического уравнения гиперболы координаты точки M x и y и значения числителя и знаменателя из уравнения асимптоты, кроме того, умножаем каждую дробь в левой части на коэффициент пропорциональности k.

Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:

Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.

Видео:§23 Построение гиперболыСкачать