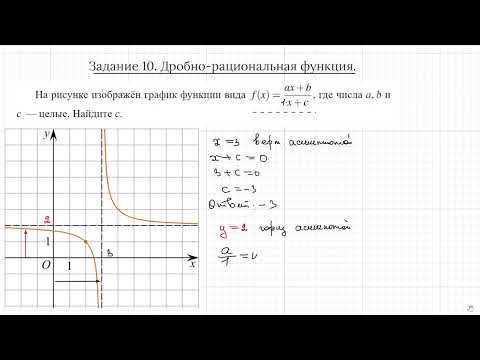
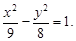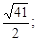Составить уравнение гиперболы оси которой совпадают с осями координат зная что (2 видео)

Составить уравнение гиперболы оси которой совпадают с осями координат зная что

Составить простейшее уравнение гиперболы, если расстояние между ее вершинами равно 20, а расстояние между фокусами 30.

Вершины параболы лежат на ее действительной оси. По условию 2a = 20; 2c = 30. Значит, a = 10; c = 15; a 2 = 100; c 2 = 225.

Величины a, b, c у гиперболы связаны соотношением

отсюда b 2 = c 2 — a 2 = 225 — 100; b 2 = 125.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Кривые второго порядка

Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных, называемых фокусами, есть величина постоянная, равная 2a, и большая чем расстояние между фокусами, равное 2c (рисунок 6).

Составить уравнение гиперболы оси которой совпадают с осями координат зная что

Рисунок 6

Простейшее каноническое уравнение эллипса получается в системе координат, в которой за ось абсцисс выбрана прямая, соединяющая фокусы, начало координат 0 − середина отрезка, концами которого служат фокусы, ось ординат – прямая, проходящая перпендикулярно оси ОX через точку 0. Тогда уравнение эллипса примет следую-
щий вид:

где

При таком выборе системы координат оси координат совпадают с осями симметрии эллипса, а начало координат − с центром симметрии. Точки А₁(a; 0), А₂(–a; 0), В₁(0; b), В₂(0; –b) называются вершинами эллипса. Отрезки, заключенные между вершинами, называются осями эллипса: большая (фокальная) ось А₁А₂ = 2a, малая ось В₁В₂ = 2b. Параметры a и b уравнения равны полуосям эллипса. Эксцентриситетом (e) эллипса называется отношение расстояния (2c) между фокусами к большей оси (2a), т. е. ; очевидно, что e

Пример 11. Составить каноническое уравнение эллипса, зная, что малая полуось равна 3 и эксцентриситет

Уравнение будем искать в виде

Из условия b = 3. Так как с одной стороны , а с другой стороны по условию то Откуда Для эллипса параметры a, b, c связаны соотношением Поэтому, подставляя значения b и c, получим уравнение

Ответ:

Тест 22. Уравнение эллипса, полуоси которого равны a = 3, b = 2, имеет вид:

Тест 23. Дано уравнение эллипса

Вычислить длину осей, фокусное расстояние, эксцентриситет:

1) 16; 9; 25;

2) 8; 6; 2

Пример 12. Дан эллипс Написать уравнение его директрис.

Уравнения директрис следующие: . Из уравнения а 2 = 36,
b 2 = 20. Следовательно, a = 6, или с = 4. Найдем e = Подставим в уравнения

Уравнение эллипса, центр которого находится в точке (х₀; у₀), а оси симметрии параллельны осям координат, имеет вид

Тест 24. Центр эллипса находится в точке:

Гиперболой называется множество точек плоскости, модуль разности от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2a, и меньшая чем расстояние между фокусами, равное 2c (рисунок 7).

Простейшее каноническое уравнение гиперболы имеет вид

(1)

Прямая, соединяющая фокусы F₁, F₂ гиперболы, служит осью абсцисс, начало координат находится в середине между фокусами; при этом оси координат совпадают с осями симметрии гиперболы, начало координат – с ее центром симметрии (оси и центр гиперболы).

Гипербола имеет две действительные вершины А₁(a; 0), А₂(–a; 0) на фокальной оси; отрезок А₁А₂ = 2a называется действительной осью гиперболы, отрезок В₁В₂ = 2b – мнимой осью гиперболы. Таким образом, параметры a и b в уравнении гиперболы равны длинам действительной и мнимой полуосей соответственно.

Если a = b, то гипербола называется равносторонней.

Если мнимая ось гиперболы имеет длину 2a и направление по оси x, а действительная ось, длиной 2b, совпадает с осью y, то уравнение такой гиперболы имеет следующий вид:

(2)

где

Гиперболы (1) и (2) называются сопряженными гиперболами.

Эксцентриситетом гиперболы называется отношение расстояния между фокусами к действительной оси: e = 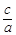и при этом e > 1. Директрисами гиперболы называются прямые, перпендикулярные к фокальной оси и отстоящие на расстоянии, равном Уравнения директрис следующие: Асимптоты гиперболы определяются равенствами

Если точка, двигаясь по гиперболе, неограниченно удаляется, то расстояние ее от одной из асимптот стремится к нулю. Асимптоты являются диагоналями прямоугольника со сторонами 2a, 2b (рисунок 7).

Пример 13.Составить уравнение гиперболы, оси которой совпадают с осями координат, зная, что:

1. Расстояние между вершинами равно 8, а расстояние между фокусами – 10.

2. Действительная ось равна 6, гипербола проходит через точку
(9; –4).

1. Уравнение гиперболы имеет вид

Так как расстояние между вершинами равно 8, то 2a = 8 или a = 4. Учитывая, что расстояние между фокусами равно 10, имеем 2c = 10, откуда c = 5. Найдем b 2 из соотношения b 2 = c 2 – а 2 , т. е. b 2 = 5 2 – 4 2 =
= 25 – 16 = 9.

Ответ:

2. Так как действительная ось равна 6, то 2a = 6 или a =3. Поэтому уравнение гиперболы принимает вид Поскольку гипербола проходит через точку (9; –4), то ординаты этой точки обращают уравнение в истинное равенство, т. е. или или 9 – 1 = или b 2 = = 2.

Ответ:

Тест 25. Уравнение гиперболы, действительная ось которой равна 10 и лежит на оси ОX, а мнимая ось равна 16 и лежит на оси ОY, имеет вид:

Тест 26. Дано уравнение гиперболы Вычислить длину осей, фокусное расстояние, эксцентриситет:

1) 10; 16; 2

2) 4; 5;

3) 5; 4;

Пример 14. Дана гипербола Написать уравнение ее директрис и асимптот.

Из уравнения а 2 = 16, b 2 = 25. Откуда a =4, b =5. Найдем Тогда уравнения директрис следующие: , или x = , или x =

Уравнения асимптот после подстановки a, b принимают вид y =

Ответ: x = y =

Тест 27. Указать, принадлежит ли точка (0; 2) гиперболе = 1:

Уравнение гиперболы, центр которой находится в точке (х₀; у₀), действительная ось совпадает с осью ОX, мнимая – с осью ОY, имеет вид

Тест 28. Центр гиперболы находится в точке:

Ответы на тестовые задания

Номер теста

Правильный ответ

Парабола

Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом параболы, и данной прямой, называемой директрисой параболы (рисунок 8).

Рисунок 8

Если за ось абсцисс принять перпендикулярную прямую, проведенную из фокуса к директрисе, а начало координат поместить посередине между фокусом и директрисой, то уравнение параболы примет вид

где р – параметр параболы, расстояние от фокуса параболы до ее директрисы.

Парабола имеет одну ось симметрии, которая совпадает при таком выборе системы координат с осью X. Единственная вершина параболы совпадает с началом координат и является единственной точкой пересечения параболы с осями.

Пример 15. Составить уравнение параболы, зная, что фокусы имеют координаты (0; 5), ось ординат служит осью симметрии, а вершина находится в начале координат.

Так как осью симметрии является ось ОY, то уравнение будет иметь вид х 2 = 2ру, так как фокус в общем случае имеет координаты , то исходя из условия имеем = 5, откуда p = 10. Таким образом, х 2 = 2 × 10 × у или х 2 = 20у – искомое уравнение.

Тест 29. В уравнении параболы у 2 = 3х значение параметра p равно:

2) ;

Тест 30. Среди уравнений второго порядка указать уравнение гиперболы:

Если вершина параболы находится в точке (x₀; y₀), то ее каноническое уравнение примет следующий вид:

Ответы на тестовые задания

Номер теста

Правильный ответ

Векторная алгебра

При изучении различных разделов экономики, механики, физики, других учебных дисциплин приходится иметь дело с величинами, для характеризации которых в выбранной системе единиц достаточно указать их численные значения. Эти величины называются скалярными. К числу скалярных величин можно отнести длину, площадь, объем, массу, температуру и т. п. Встречаются, тем не менее, такие величины, для определения которых необходимо знать их направления в пространстве. Указанные величины будем называть векторными. Примерами векторных величин являются сила, скорость, ускорение.

Геометрические векторные величины изображаются с помощью направленных отрезков.

Связанным вектором (или направленным отрезком) называется любой отрезок прямой, если только указано, какая из двух ограничивающих его точек является начальной, какая – конечной. Если точка А – начало отрезка, а точка В – его конец, то связанный вектор будем обозначать Его направление будем указывать стрелкой, идущей от начала А к концу В.

Длиной (или модулем) связанного вектора называется длина отрезка АВ. Связанный вектор, у которого начало и конец совпадают, называется нулевым. Нулевой вектор обозначается 0, его длина равна 0: он направления не имеет.

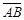
Связанные векторы 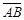и называются сонаправленными, если являются сонаправленными лучи и противоположно направленными – если противоположно направлены эти лучи.

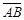
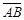
Два ненулевых связанных вектора и назовем равными (это обозначается = ), если они сонаправлены и имеют одинаковую длину.

Свободным вектором а (или просто вектором) назовем множество равных между собой связанных векторов. При дальнейшем из контекста будет ясно, какой вектор имеется в виду (связанный или свободный). Для задания вектора достаточно указать какой-либо один вектор из всего множества <AB, CD, MN, ¼> равных связанных векторов, например, 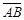(рисунок 9).

Рассмотренные понятия (длина, направление и т. п.), которые введены для связанных векторов, имеют аналоги также и для свободных. Часто векторы обозначают одной жирной строчной буквой: 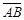= а (рисунок 10).

Линейные операции над векторами

Определим для свободных векторов операции их сложения, вычитания, умножения вектора на действительное число.

Суммой двух векторов a и b по правилу треугольника называется такой третий вектор с, что начало его совпадает с началом вектора а, а конец – с концом вектора b.

Иногда вместо с = а+bпишут Суммой а₁ +а₂ +…
… + а_n конечного числа векторов называется такой вектор а, который замыкает ломаную линию, построенную из данных векторов а₁, а₂,…, а_n таким образом, что начало каждого последующего вектора совпадает с концом предыдущего. Указанный вектор а направлен из начала первого вектора суммы в конец последнего (правило многоугольника) (рисунок 10).

c = a + b

На рисунке 11 изображена сумма а = а₁ + а₂ + а₃ + а₄ + а₅ векторов а₁, а₂, а₃, а₄, а₅.

Произведением вектора а на число a называется вектор b = a а, длина которого равна направление которого совпадает с направлением а, если a > 0, и противоположно направлению а, если
a 0 будем обозначать единичный вектор, имеющий направление вектора а.

Видео:Видеоурок "Гипербола"Скачать

2.4 Гипербола

Гиперболой Называется геометрическое место точек на плоскости, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная.

Обозначим эту постоянную через 2А, расстояние между фокусами через 2С, а оси координат выберем так же, как в разделе 2.3.

Пусть М(Х, У) – произвольная точка гиперболы (рисунок 2.4).

По определению гиперболы F2M – F1М = ±2A. (Знак плюс в правой части надо выбрать, если F2M > F1М, и минус, если F2M A).

Исследуем формулу гиперболы.

1. Уравнение (2.7) содержит квадраты текущих координат, следовательно, оси координат являются осями симметрии гиперболы. Ось симметрии, на которой находятся фокусы, называется фокальной осью, точка пересечения осей симметрии – центром гиперболы. Для гиперболы, заданной уравнением (2.7), фокальная ось совпадает с осью ОХ, а центр – с началом координат.

В этом случае координаты фокусов гиперболы имеют вид F1(с,0), F2(-с,0).

2. Точки пересечения с осями симметрии. Точки пересечения гиперболы с осями симметрии называются Вершинами гиперболы. Полагая в уравнении (2.7) У = 0, найдем абсциссы точек пересечения с осью ОХ:

или X2 = А2, откуда Х = ±А.

Итак, точки и являются вершинами гиперболы.

Если же в уравнении (2.7) принять x = 0, получим

или У2 = –B2,

Т. е. для У мы получили мнимые значения. Это означает, что гипербола не пересекает ось ОY.
В соответствии с этим ось симметрии, пересекающая гиперболу, называется действительной осью (фокальная ось); ось симметрии, которая не пересекает гиперболу, – ее мнимой осью. Для гиперболы, заданной уравнением (2.7), действительной осью симметрии является ось ОХ, а мнимой осью – ось ОY. Длина отрезка А1А2 = 2А, число А называется действительной полуосью гиперболы. Отложим на мнимой оси гиперболы по обе стороны от центра симметрии O отрезки ОВ1 и ОВ2 длиною B, тогда отрезок В1B2 = 2B называют мнимой осью, а величину B – мнимой полуосью гиперболы.

Из уравнения (2.7) видно, что , следовательно, |X| ³ A. Кривая имеет форму, изображенную на рисунке 2.5. Она располагается вне прямоугольника со сторонами, равными 2А и 2B, с центром в начале координат, и состоит из двух отдельных ветвей, простирающихся в бесконечность (см. рисунок 2.5). Диагонали этого прямоугольника определяются уравнениями

(2.8)

И являются Асимптотами гиперболы.

Если A = B, гипербола называется равносторонней.

Замечание 1. Если мнимая ось гиперболы равна 2А и расположена на оси ОХ, а действи-тельная ось равна 2B и расположена на оси ОY, то уравнение такой гиперболы (рисунок 2.6) имеет вид (каноническое уравнение гиперболы, если ее фокальная ось – ось Y)

(2.9)