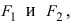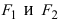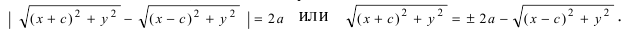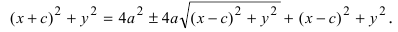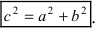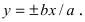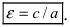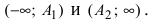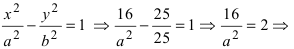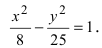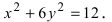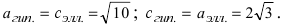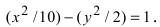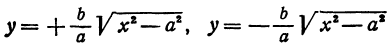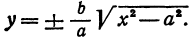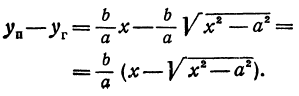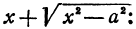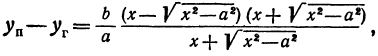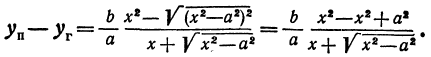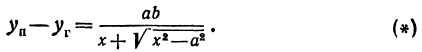Гипербола:
Определение: Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек
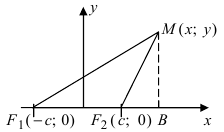
Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы
Рис. 31. Вывод уравнения гиперболы.
Расстояние между фокусами (фокусное расстояние) равно 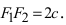
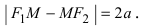
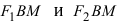
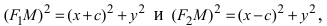
Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 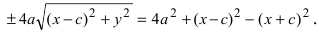
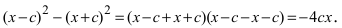
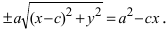
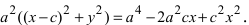
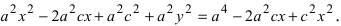
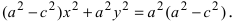
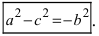
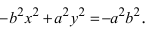
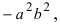
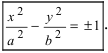
Проанализируем полученное уравнение. Если точка М(х;у) принадлежит гиперболе, то ей принадлежат и симметричные точки 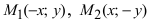
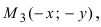
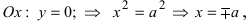
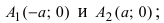
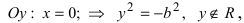
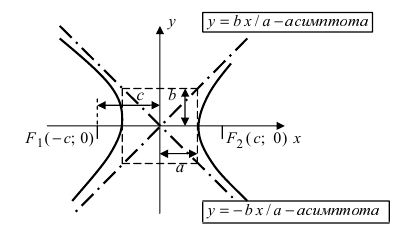
Рис. 32. Асимптоты и параметры гиперболы
Определение: Найденные точки 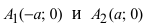
Докажем, что при возрастании (убывании) переменной х гипербола неограниченно приближается к прямым 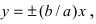
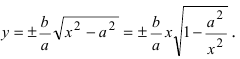
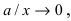
Определение: Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.
В данном конкретном случае параметр а называется действительной, а параметр b — мнимой полуосями гиперболы.
Определение: Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы
Из определения эксцентриситета гиперболы следует, что он удовлетворяет неравенству 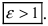
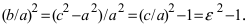
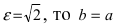
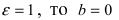
Пример:
Составить каноническое уравнение гиперболы, если мнимая полуось b = 5 и гипербола проходит через точку М(4; 5).
Решение:
Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины:
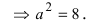
Пример:
Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах эллипса
Решение:
Для определения координат фокусов и вершин эллипса преобразуем его уравнение к каноническому виду. Эллипс: 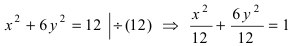
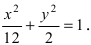
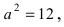
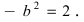
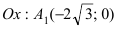
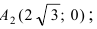
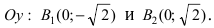
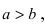
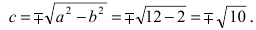
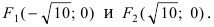
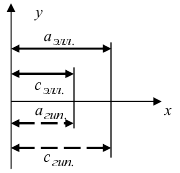
Рис. 33. Параметры эллипса и гиперболы
Вычислим длину мнимой полуоси 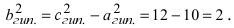
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Гипербола в высшей математике
Решая его относительно 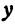
или одну двузначную функцию
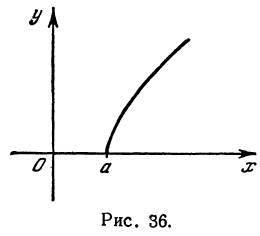
Функция 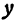

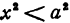
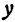
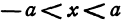
При 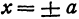
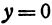
При 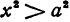
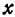
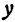
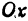
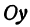
Кривая, все точки которой имеют координаты, удовлетворяющие уравнению (3), называется гиперболой.
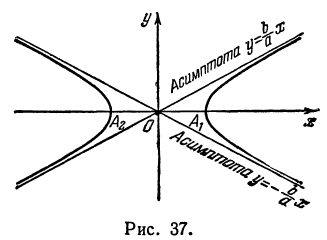
Гипербола в силу симметрии имеет вид, указанный на рис. 37.
Точки пересечения гиперболы с осью 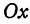
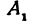
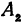
Часть гиперболы, расположенная в первой и четвертой четвертях, называется правой ветвью, а часть гиперболы, расположенная во второй и третьей четвертях, — левой ветвью.
Рассмотрим прямую, заданную уравнением 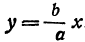
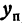
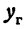
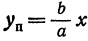
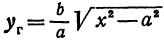
Умножим и разделим правую часть на
Будем придавать 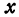
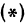

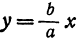
Вследствие симметрии видно, что часть правой ветви, расположенная в четвертой четверти, будет приближаться к прямой, определяемой уравнением 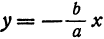
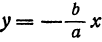
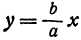
Прямая, к которой неограниченно приближается гипербола при удалении от начала координат, называется асимптотой гиперболы.
Таким образом, гипербола имеет две асимптоты, определяемые уравнениями 
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Эллипс
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Сборник задач по линейной алгебре и аналитической геометрии Учебное пособие (стр. 8 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 |
15.25. Составить уравнение эллипса, если известны его эксцентриситет 
15.26. Найти точки пересечения прямой х+2у-7=0 и эллипса х2+4у2=25.
15.27. Найти точки пересечения прямой 3х+10у-25=0 и эллипса 
15.28. Найти точки пересечения прямой 3х-4у-40=0 и эллипса 
15.29. Определить, при каких значениях m прямая у = — х + m 1)пересекает эллипс 
15.30. Составить уравнение касательной к эллипсу 
16.1. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, кроме того, что ее полуоси 

16.2. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, если расстояние между фокусами 2с=10 и эксцентриситет 
16.3. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, если уравнения асимптот у = 
16.4. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если расстояние между директрисами равно 

16.5. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, если расстояние между директрисами равно 

16.6. Дана гипербола 16х2-9у2 = -144. Найти 1)полуоси 
16.7. Вычислить площадь треугольника, образованного асимптотами гиперболы 
16.8. Дана гипербола 

16.9. Эксцентриситет гиперболы 
16.10.Эксцентриситет гиперболы 
16.11. Эксцентриситет гиперболы 
16.12. Эксцентриситет гиперболы 
16.13. Определить точки гиперболы 
16.14. Определить точки гиперболы 
16.15. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны точки М1(6,-1) и М2(
16.16. Составить уравнение гиперболы, фокусы которой лежат на оси ординат симметрично относительно начала координат, если даны точка гиперболы и эксцентриситет 
16.17. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс, симметрично относительно начала координат, если даны точка М 

16.18. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, если даны точка М1 

16.19. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметрично относительно начала координат, если даны уравнения асимптот у = 

16.20. Фокусы гиперболы совпадают с фокусами эллипса 

16.21. Составить уравнения гиперболы, фокусы которой лежат в вершинах эллипса 
16.22. Найти центр, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис гиперболы 16х2-9у2-64х-54у-161=0.
16.23. Найти центр, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис гиперболы 9х2-16у2+90х+32у-367=0.
16.24. Составить уравнения гиперболы, зная, что расстояние между ее вершинами равно 24 и фокусы F1(-10,2) и F2(16,2).
16.25. Составить уравнение гиперболы, зная, что фокусы F1(3,4) и F2(-3,-4) и расстояние между директрисами равно 3,6.
16.26. Составить уравнение гиперболы, если угол между асимптотами равен 90˚ и фокусы F1(4,-4) и F2(-2,2).
16.27. Составить уравнение гиперболы, если известны ее эксцентриситет 
16.28. Найти точки пересечения прямой 2х-у-10=0 и гиперболы 
16.29. Найти точки пересечения прямой 4х-3у-16=0 и гиперболы 
17.1. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена симметрично относительно оси ОХ и проходит через точку А(9,6).
17.2. Составить уравнение параболы, вершина которой находится в начале координат, если парабола расположена симметрично оси ОХ и проходит через точку В(-1,3).
17.3. Составить уравнение параболы, вершина которой находится в начале координат, если парабола расположена симметрично относительно оси ОУ и проходит через точку С(1,1).
17.4. Составить уравнения параболы, вершина которой находится в начале координат, если парабола расположена симметрично относительно оси ОУ и проходит через точку D(4,-8).
17.5. Найти фокус F и уравнение директрисы параболы у2=24х.
17.6. Вычислить фокальный радиус точки М параболы у2=20х, если абсцисса точки М равна 7.
17.7. Вычислить фокальный радиус точки М параболы у2=12х, если ордината точки М равна 6.
17.8. На параболе у2=16х найти точки, фокальный радиус которых равен 13.
17.9. Составить уравнение параболы, если дан фокус F(-7,0) и уравнение директрисы х-7=0.
17.10. Найти вершину параболы и ее параметр у2=4-6х.
17.11. Найти вершину и параметр параболы х=-у2+2у-1.
17.12. Составить уравнение параболы, если даны ее фокус F(7,2) и директриса х-5=0.
17.13.Составить уравнение параболы, если ее фокус F(4,3) и директриса у+1=0.
17.14. Составить уравнение параболы, если даны ее фокус F(2,-1) и директриса х-у-1=0.
17.15. Даны вершина параболы А(6,-3) и уравнение ее директрисы
3х-5у+1=0. Найти фокус F этой параболы.
17.16. Даны вершина параболы (-2,-1) и уравнение ее директрисы х+2у-1=0. Составить уравнение этой параболы.
17.17. Определить точки пересечения прямой х+у-3=0 и параболы х2=4у.
17.18. Определить точки пересечения прямой 3х+4у-12=0 и параболы у2=-9х.
17.19. Определить точки пересечения прямой 3х-2у+6=0 и параболы у2=6х.
17.20. Определить при каких значениях углового коэффициента kпрямая
у = kх+2 а)пересекает параболу у2=4х, б)касается ее, в)проходит вне этой параболы.
17.21. Составить уравнение прямой, которая касается параболы у2=8х и параллельна прямой 2х+2у-3=0.
Видео:Видеоурок "Гипербола"Скачать

Гипербола: формулы, примеры решения задач
Видео:213. Фокус и директриса параболы.Скачать

Определение гиперболы, решаем задачи вместе
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:

где a и b — длины полуосей, действительной и мнимой.
На чертеже ниже фокусы обозначены как 

На чертеже ветви гиперболы — бордового цвета.
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки 


называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:

Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет 
Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет — это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:

Результат — каноническое уравнение гиперболы:
Если 




Если 




На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

называются директрисами гиперболы (на чертеже — прямые ярко-красного цвета).
Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

где 





Пример 4. Дана гипербола 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. 

Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.
Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями

На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:


В том случае, когда угол между асимптотами — прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы 

Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения 

Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Видео:Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) b = 4 , а один из фокусов в точке (5; 0)
2) действительная ось 6, расстояние между фокусами 8
3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы
🌟 Видео
§29 Эксцентриситет гиперболыСкачать

Овчинников А. В. - Аналитическая геометрия - Эллипс, гипербола, параболаСкачать

Фокусы гиперболыСкачать

Вариант 72, № 5. Уравнение оси симметрии параболы. Пример 2Скачать

§23 Построение гиперболыСкачать

Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

§21 Каноническое уравнение гиперболыСкачать

Неполное уравнение второго порядка. Эллипс, гипербола. ЗадачиСкачать

Как легко составить уравнение параболы из графикаСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

ЭллипсСкачать

ГиперболаСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Шишкин А. А. - Аналитическая геометрия - Кривые второго порядкаСкачать

Фокус и директриса параболы 1Скачать