Составить уравнение эллипса фокусы которого лежат на оси ординат симметрично начала координат

Видео:Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, зная, кроме того, что его большая ось равна 10, а расстояние между фокусами равно 8?

Геометрия | 10 — 11 классы

Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, зная, кроме того, что его большая ось равна 10, а расстояние между фокусами равно 8.

Найти эксцентриситет, координаты фокусов и уравнения директрис получившегося эллипса.

F1 — F2 = 2c = 8 c = 4

большаяось2b = 10 b = 5

a ^ 2 = b ^ 2 — c ^ 2 a ^ 2 = 25 — 16 = 9 a = 3

уравнениеэлипсаx ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 x ^ 2 / 9 + y ^ 2 / 25 = 1

эксцентриситет = c / b = 4 / 5

уравнениядиректрисх = + — а / е х = + — (3 * 5) / 4 = + — 15 / 4 = + — 3 3 / 4

координатыфокусов(0 ; 4) (0 ; — 4).

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Составить уравнения общих касательных двух эллипсов и ?

Составить уравнения общих касательных двух эллипсов и .

Видео:ЭллипсСкачать

Чему равны координаты точки, симметричной точке ( — 4 ; 2) относительно оси x?

Чему равны координаты точки, симметричной точке ( — 4 ; 2) относительно оси x.

Видео:Видеоурок "Эллипс"Скачать

Построить параболу, ее директрису и фокус зная каноническое уравнение параболы : x ^ 2 = 6y?

Построить параболу, ее директрису и фокус зная каноническое уравнение параболы : x ^ 2 = 6y.

Видео:Уравнение эллипсаСкачать

Прямая задана уравнением 2x — 3y = 0 записать уравнение прямой, симметричной данной относительно начала координат?

Прямая задана уравнением 2x — 3y = 0 записать уравнение прямой, симметричной данной относительно начала координат.

Видео:Эллипс. Определение. Уравнение. График. Фокусы. Главные оси. Эксцентриситет - Новиков АлександрСкачать

Помогите?

☻☺ Точка А(а ; — 3) симметрична точке В(4 ; b) ОТНОСИТЕЛЬНО : а)оси абсцисс ; б) оси ординат ; в)начала координат.

Найдите значения a и b.

Видео:11 класс, 52 урок, ЭллипсСкачать

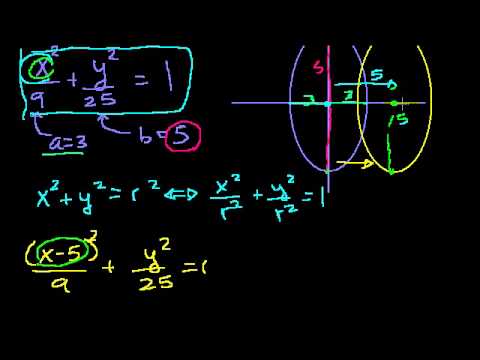
Прямая задана уравнением 2x — 3y = 0 записать уравнение прямой, симметричной данной относительно начала координат?

Прямая задана уравнением 2x — 3y = 0 записать уравнение прямой, симметричной данной относительно начала координат.

Видео:§28 Эксцентриситет эллипсаСкачать

Составьте каноническое уравнение гиперболы с асимптотами x — 2y — 3 = 0 и x + 2y + 1 = 0, если расстояние между её фокусами равно 20?

Составьте каноническое уравнение гиперболы с асимптотами x — 2y — 3 = 0 и x + 2y + 1 = 0, если расстояние между её фокусами равно 20.

Помогите решить это.

Видео:Видеоурок "Гипербола"Скачать

Запишите уравнение прямой, проходящей через точки, которые симметричны точкам К( — 4 ; 2) и М(3 ; — 5) относительно начала координат?

Запишите уравнение прямой, проходящей через точки, которые симметричны точкам К( — 4 ; 2) и М(3 ; — 5) относительно начала координат.

Видео:Овчинников А. В. - Аналитическая геометрия - Эллипс, гипербола, параболаСкачать

Чему равны координаты точке, симметричной точке Р ( — 6 ; 8)относительно оси обсцисс?

Чему равны координаты точке, симметричной точке Р ( — 6 ; 8)относительно оси обсцисс.

Помогите пожалуйста, срочно!

Видео:Фокусы эллипсаСкачать

Укажите координаты точки, симметричной точке К(2 ; — 5) относительно оси ординат?

Укажите координаты точки, симметричной точке К(2 ; — 5) относительно оси ординат.

На странице вопроса Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, зная, кроме того, что его большая ось равна 10, а расстояние между фокусами равно 8? из категории Геометрия вы найдете ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Если в условии задачи сказано, что диагонали равны, то решение такое.

В этой задаче отношение оснований трапеции совершенно не нужно. Удвоенная средняя линия — это сумма оснований, значит, 82 — 60 = 22 — сумма боковых сторон, одна сторона 11, так как трапеция равнобедренная. Не знаю, зачем Вам чертеж, но эскиз получа..

Ответ : Объяснение : Длина вектора определяется по формуле : Значит для вектора b.

Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Составить уравнение эллипса фокусы которого лежат на оси ординат симметрично начала координат

Вопрос по геометрии:

Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, зная, кроме того, что его большая ось равна 10, а расстояние между фокусами равно 8. Найти эксцентриситет, координаты фокусов и уравнения директрис получившегося эллипса.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

F1 — F2 =2c=8 c=4
большая ось 2b=10 b=5
a^2=b^2 — c^2 a^2=25 — 16 =9 a=3

уравнение элипса x^2/a^2 + y^2/b^2 =1 x^2/9 +y^2/25=1

эксцентриситет = c/b = 4/5

уравнения директрис х=+- а/е х=+-(3*5)/4 =+-15/4=+- 3 3/4

координаты фокусов (0;4) (0; -4)

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Составить уравнение эллипса фокусы которого имеют координаты

Определение. Эллипс – это геометрическая фигура, которая ограничена кривой, заданной уравнением .

Он имеет два фокуса. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

Видео:Полярные координаты. Полярное уравнение эллипса.Скачать

Чертеж фигуры эллипс

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема. Фокусное расстояние и полуоси связаны соотношением:

Доказательство: В случае, если точка М находится на пересечении эллипса с вертикальной осью, r₁ + r₂ = 2*(по теореме Пифагора). В случае, если точка М находится на пересечении его с горизонтальной осью, r₁ + r ₂ = a – c + a + c. Т.к. по определению сумма r₁ + r ₂ – постоянная величина, то , приравнивая, получаем:

Видео:Уравнение эллипса. Нахождение вершин и фокусовСкачать

Эксцентриситет фигуры эллипс

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом .

Если a = b ( c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

Если для точки М(х ₁ , у ₁ ) выполняется условие: , то она находится внутри эллипса, а если , то точка находится вне его.

Теорема. Для произвольной точки М(х, у), принадлежащей фигуре эллипс верны соотношения :

Доказательство. Выше было показано, что r₁ + r₂ = 2 a . Кроме того, из геометрических соображений можно записать:

После возведения в квадрат и приведения подобных слагаемых:

Аналогично доказывается, что r₂ = a + ex . Теорема доказана.

Видео:Разбор задания из теста по ангему | Уравнение эллипса | Уравнение касательной к эллипсуСкачать

Директрисы фигуры эллипс

С фигурой эллипс связаны две прямые, называемые директрисами . Их уравнения:

x = a / e ; x = – a / e .

Теорема. Для того, чтобы точка лежала на границе фигуры эллипс, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину фигуры эллипс, заданного уравнением :

• Координаты нижней вершины: x = 0; y 2 = 16; y = -4.

• Координаты левого фокуса: c 2 = a 2 – b 2 = 25 – 16 = 9; c = 3; F₂ (-3; 0).

• Уравнение прямой, проходящей через две точки:

Пример. Составить уравнение границы фигуры эллипс, если его фокусы F ₁ (0; 0), F₂ (1; 1), большая ось равна 2.

Уравнение границы имеет вид: . Расстояние между фокусами:

2 c = , таким образом, a 2 – b 2 = c 2 = 1/2

по условию 2а = 2, следовательно а = 1, b =

Итого искомое уравнение имеет вид: .

УСЛОВИЕ:

Составить уравнение эллипса, зная, что:
а) его большая полуось равна 10 и фокусы суть F1(-6;0), F2(10;0)
б) а=5, F1(-3;5), F2(3;5)
2.
Составить каноническое уравнение эллипса, фокусы которого расположены на оси Ох, симметрично относительно начала координат, если:
а)задана точка M1(2 корня из 3;1) эллипса и его малая полуось равна 2
б) заданы две точки эллипса M1(0;7) и M2(8;0)
в)расстояние между фокусами равно 24 и большая ось равна 26
г) экцентриситет равен 7/25 и заданы фокусы (+-7;0)

Добавил maryney23 , просмотры: ☺ 3749 ⌚ 2018-12-29 21:53:45. предмет не задан класс не задан класс

Решения пользователей

РЕШЕНИЕ ОТ sova

M- середина F_(1)F_(2)
x_(M)=(-6+10)/2=2
y_(M)=0
M(2;0)
Прямая x=2 -оcь симметрии эллипса

О т в е т.(x-2)^2/(10^2)+(y^2/6^2)=1

б) F_(1)(-3;5); F_(2)=(3;5)⇒
c=3
Прямая
y=5 – ось симметрии эллипса

О т в е т.(x^2/5^2)+((y-5)^2/4^2)=1

2. Если фокусы эллипса расположены на оси Ох, симметрично относительно начала координат, то каноническое уравнение эллипса имеет вид
(x^2/a^2)+(y^2/b^2)=1

а)
b=2
(x^2/a^2)+(y^2/4)=1
Подставляем координаты точки M_(1):
(12/a^2)+(1/4)=1
(12/a^2)=3/4
a^2=16
О т в е т. (x^2/4^2)+(y^2/2^2)=1

О т в е т. (x^2/8^2)+(y^2/7^2)=1

в)
2с=24 ⇒ с=12
2а=26 ⇒ а=13

b^2=a^2-с^2=13^2-12^2=169-144=25=5^2
О т в е т. (x^2/13^2)+(y^2/5^2)=1

г)
F( ± c;0) ⇒ c=7
ε=с/а
c/a=7/25
a=25
b^2=a^2-c^2=625-49=576=24^2
О т в е т. (x^2/25^2)+(y^2/24^2)=1

Консультации и решение задач по алгебре, геометрии, анализу, дискретной математике.

Лучшие эксперты в этом разделе

Коцюрбенко Алексей Владимирович Статус: Модератор Рейтинг: 1702

epimkin Статус: Бакалавр Рейтинг: 385

Roman Chaplinsky / Химик CH Статус: Модератор Рейтинг: 372

здравствуйте помогите пожалуйста.
Составить уравнение эллипса, фокусы которого имеют координаты (0;4√2) и (0;- 4√2) , а малая ось равна 14. спасибо за помощь

Состояние: Консультация закрыта

Здравствуйте, анисимова юлия александровна!
Уравнение эллипса имеет вид
x²/a² + y²/b² = 1 (если фокусы расположены на оси Ox)
или
x²/b² + y²/a² = 1 (если фокусы расположены на оси Oy).
У нас второй случай.

Фокусы эллипса имеют координаты (0; 4√2) и (0; -4√2), значит, c = 4√2.
Малая ось равна 14, т.е. b = 14.
У эллипса
a² = b² + c².
Значит,
a² = 196 + 32 = 228.

Ответ: x²/196 + y²/228 = 1.

Консультировал: Агапов Марсель Дата отправки: 15.01.2008, 22:17

0

Отправлять сообщения
модераторам могут
только участники портала.
ВОЙТИ НА ПОРТАЛ »
регистрация »

Возможность оставлять сообщения в мини-форумах консультаций доступна только после входа в систему.
Воспользуйтесь кнопкой входа вверху страницы, если Вы зарегистрированы или пройдите простую процедуру регистрации на Портале.

🎬 Видео

найти уравнение касательной к эллипсуСкачать

Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

§18 Каноническое уравнение эллипсаСкачать