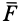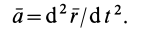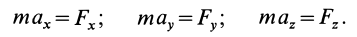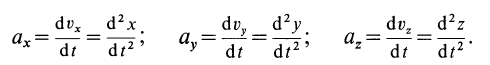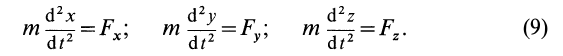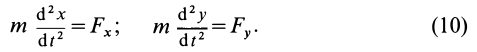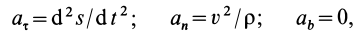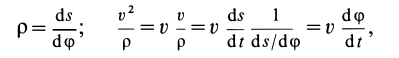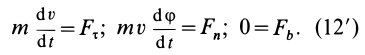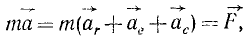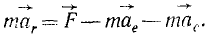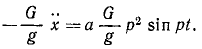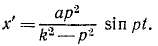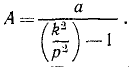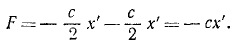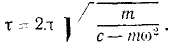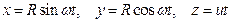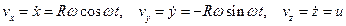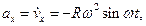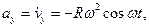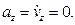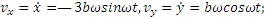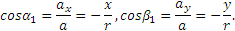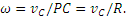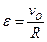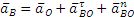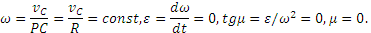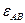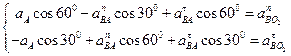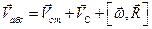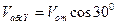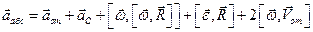Содержание:
Дифференциальные уравнения движения материальной точки:
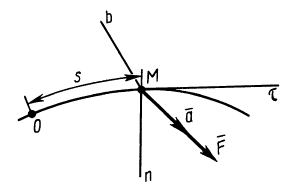
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
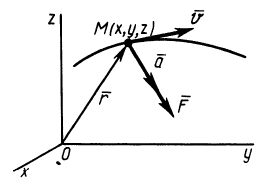
Из кинематики точки известно, что ускорение 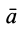
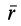
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
- Частные случаи дифференциального уравнения движения материальной точки
- Дифференциальные уравнения относительного движения точки
- Пример решения задачи №1
- Пример решения задачи №2
- Пример решения задачи №3
- Примеры решения задач. Движение точки задано уравнениями (х, у — в метрах, t — в секундах).
- Теоретическая механика: Решебник Яблонского: Кинематика твердого тела (К2, К3, К4, К5, К6)
- Задание К.2. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях
- Задание К.3. Кинематический анализ плоского механизма
- Задание К.4. Кинематический анализ многозвенного механизма
- Задание К.5. Определение кинематических характеристик движения твердого тела и его точек по уравнениям Эйлера
- Задание К.6. Кинематический анализ движения твердого тела, катящегося без скольжения по неподвижной поверхности и имеющего неподвижную точку
- 🔍 Видео
Видео:К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 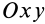
Так как 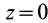
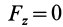
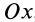
Так как при движении 
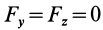
где 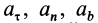
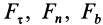
где 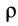
Второе уравнение из (12) можно преобразовать:
где 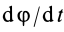
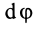
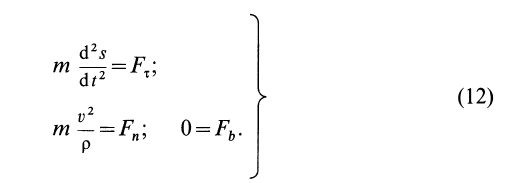
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 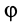
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
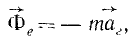
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
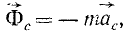
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
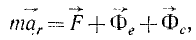
или в проекциях на оси координат:
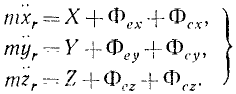
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
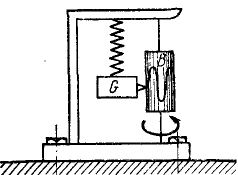
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 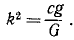
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 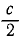
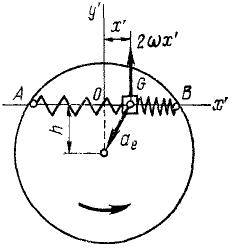
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 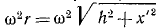
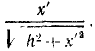
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 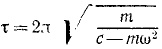
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Уравнение движенияСкачать

Примеры решения задач. Движение точки задано уравнениями (х, у — в метрах, t — в секундах).
Задача 2.1.
Движение точки задано уравнениями (х, у — в метрах, t — в секундах).
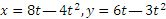
Определить траекторию, скорость и ускорение точки.
Решение.
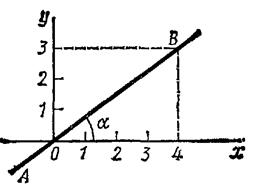 |
| Рис. 2.9. К задаче 2.1 |
Для определения траектории исключаем из уравнений движения время t. Умножая обе части первого уравнения на 3, а обе части второго — на 4 и почленно вычитая из первого равенства второе, получим: 
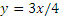
Следовательно, траектория — прямая линия, наклоненная к оси Ох под углом α, где 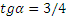
Определяем скорость точки. По формулам (2.1) получаем:
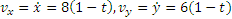
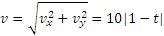
Теперь находим ускорение точки. Формулы (2.1) дают:
Направлены векторы 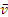
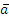
Заметим, наконец, что при 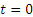
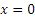
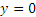
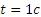
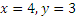
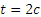
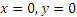
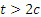
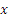
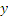
Итак, заданные в условиях задачи уравнения движения рассказывают нам всю историю движения точки. Движение начинается из точки О с начальной скоростью 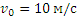
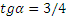
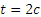
Задача 2.2.
Движение точки задано уравнениями:
где 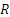
Решение.
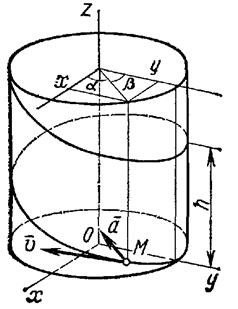 |
| Рис. 2.10. К задаче 2.2 |
Возводя первые два уравнения почленно в квадрат и складывая, получаем
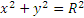
Следовательно, траектория лежит на круглом цилиндре радиуса R, ось которого направлена вдоль оси Oz (рис. 2.10). Определяя из последнего уравнения t и подставляя в первое, находим
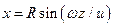
Таким образом, траекторией точки будет линия пересечения синусоидальной поверхности, образующие которой параллельны оси Оу (синусоидальный гофр) с цилиндрической поверхностью радиуса R. Эта кривая называется винтовой линией. Из уравнений движения видно, что один виток винтовой линий точка проходит за время 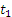
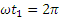
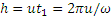
Найдем скорость и ускорение точки. Дифференцируя уравнения движения по времени, получаем:
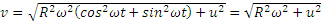
Стоящие под знаком радикала величины постоянны. Следовательно, движение происходит с постоянной по модулю скоростью, направленной по касательной к траектории. Теперь по формулам (2.1) вычисляем проекции ускорения;
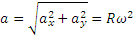
Итак, движение происходит с постоянным по модулю ускорением, Для определения направления ускорения имеем формулы:
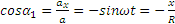
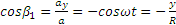
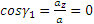
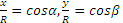
где α и β —углы, образуемые с осями Ох и Оу радиусом R, проведенным от оси цилиндра к движущейся точке. Так как косинусы углов α1 и β1 отличаются от косинусов α и β только знаками, то отсюда заключаем, что ускорение точки все время направлено по радиусу цилиндра к его оси.
Заметим, что хотя в данном случае движение и происходит со скоростью, постоянной по модулю, ускорение точки не равно нулю, так как направление скорости изменяется.
Задача 2.3.
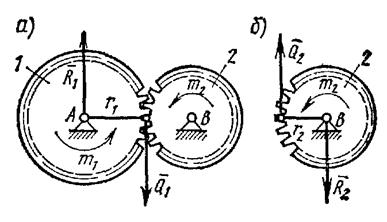
На шестерню 1 радиуса r1 действует пара сил с моментом m1 (рис. 46, а). Определить момент m2 пары, которую надо приложить к шестерне 2 радиуса r2, чтобы сохранить равновесие.
Решение.
 |
| Рис. 2.11. К задаче 2.3 |
Рассмотрим сначала условия равновесия шестерни 1. На нее действует пара с моментом m1, которая может быть уравновешена только действием другой пары, в данном случае пары 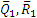
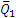
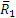
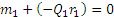
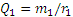
Теперь рассмотрим условия равновесия шестерни 2 (рис. 46, б). По закону равенства действия и противодействия на нее со стороны шестерни 1 будет действовать сила 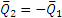
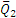
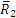
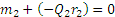
Естественно, что пары с моментами m1 и m2 не удовлетворяют условию равновесия , так как они приложены к разным телам.
Полученная в процессе решения задачи величина Q1 (или Q2) называется окружным усилием, действующим на шестерню. Как видим, окружное усилие равно моменту вращающей пары, деленному на радиус шестерни: Q1=m1/r1 =m2/r2.
Задача 2.4.
Человек ростом h удаляется от фонаря, висящего на высоте H, двигаясь прямолинейно со скоростью 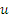
Решение.
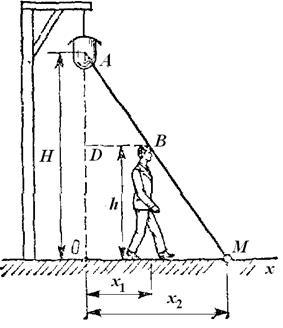 |
| Рис. 2.12. К задаче 2.4 |
Для решения задачи найдем сначала закон, по которому движется конец тени. Выбираем начало отсчета в точке О, находящейся на одной вертикали с фонарем, и направляем вдоль прямой, по которой движется конец тени, координатную ось Ох (рис. 2.12). Изображаем человека в произвольном положении на расстоянии x1 от точки О. Тогда конец его тени будет находиться от начала О на расстоянии х2.
Из подобия треугольников ОАМ и DAB находим:

Это уравнение выражает закон движения конца тени М, если закон движения человека, т.е. 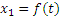
Взяв производную по времени от обеих частей равенства и замечая, что по формуле (2.1) 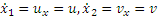
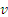
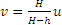
Если человек движется с постоянной скоростью ( 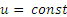
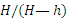
Обращаем внимание на то, что при составлении уравнений движения надо изображать движущееся тело или механизм в произвольном положении. Только тогда мы поучим уравнения, определяющие положение движущейся точки (или тела) в любой момент времени.
Задача 2.5.
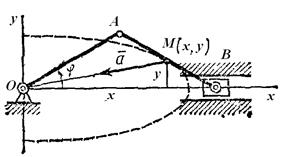
Определить траекторию, скорость и ускорение середины М шатуна кривошипно-ползунного механизма (рис. 2.13), если OA=AB=2b, а угол 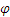
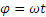
 |
| Рис. 2.13. К задаче 2.5. |
Начинаем с определения уравнений движения точки М. Проводя оси и обозначая координаты точки М в произвольном положении через х и у находим
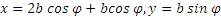
Заменяя 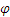
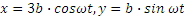
Для определения траектории точки М представим уравнения движения в виде
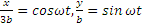
Возводя эти равенства почленно в квадрат и складывая, получим
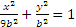
Итак, траектория точки М — эллипс с полуосями 3b и b.
Теперь по формуле (2.1) находим скорость точки М:
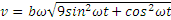
Скорость оказывается величиной переменной, меняющейся с течением времени в пределах от 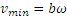
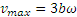
Далее по формулам (2.1) определяем проекции ускорения точки М;
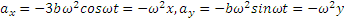
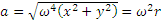
где 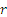
Определелим направление ускорения
Отсюда находим, что ускорение точки М все время направлено вдоль МО к центру эллипса.
Задача 2.6.
Вал, делающий n=90 об/мин, после выключения двигателя начинает вращаться равнозамедленно и останавливается через t1=40 с. Определить, сколько оборотов сделал вал за это время.
Решение.
Так как вал вращается равнозамедленно, то для него, считая 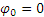
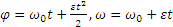
Начальной угловой скоростью при замедленном вращении является та, которую вал имел до выключения двигателя. Следовательно,
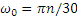
В момент остановки при t=t1 угловая скорость вала ω1=0. Подставляя эти значения во второе из уравнений (2.2), получаем:
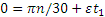
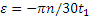
Если обозначить число сделанных валом за время t1 оборотов через N (не смешивать с n; n — угловая скорость), то угол поворота за то же время будет равен 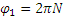
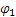
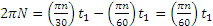
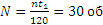
Задача 2.7.
Маховик радиусом R=0,6 м вращается равномерно, делая n=90 об/мин. Определить скорость и ускорение точки, лежащей на ободе маховика.
Решение.
Скорость точки обода 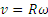
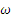
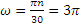
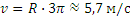
Далее, так как 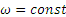
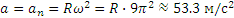
Ускорение точки направлено в данном случае к оси вращения.
Задача 2.8.
Найти скорость точки М обода колеса, катящегося по прямолинейному рельсу без скольжения (рис. 2.14), если скорость центра С колеса равна 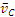
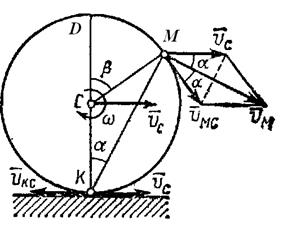 |
| Рис. 2.14. К задаче 2.8. |
Решение
Приняв точку С, скорость которой известна, за полюс, найдем, что 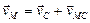
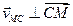
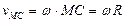
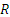
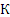
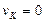
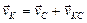
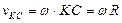
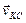
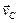
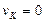
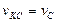
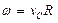
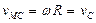
Параллелограмм, построенный на векторах 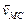
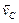
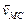
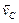
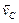
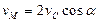
Задача 2.9.
Определить скорость точки М обода катящегося колеса, рассмотренного в предыдущей задаче, с помощью мгновенного центра скоростей.
Решение.
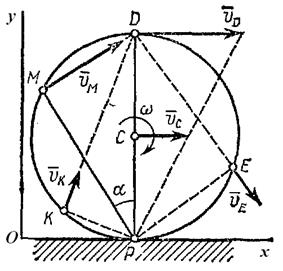 |
| Рис. 2.15. К задаче 2.9. |
Точка касания колеса Р (рис. 2.15) является мгновенным центром скоростей, поскольку 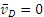
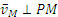
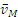
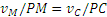
что 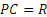
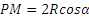
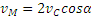
Чем точка М дальше от Р, тем ее скорость больше; наибольшую скорость 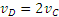
Аналогичная картина распределения скоростей имеет место при качении колеса или шестерни по любой цилиндрической поверхности.
Задача 2.10.
Центр О колеса, катящегося по прямолинейному рельсу (рис. 2.16), имеет в данный момент времени скорость 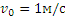
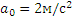
Решение.
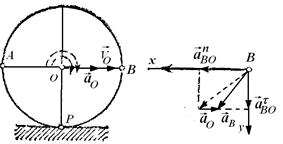 |
| Рис. 2.16. К задаче 2.10. |
1) Так как 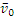
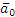
2) Определение ω. Точка касания Р является мгновенным центром скоростей; следовательно, угловая скорость колеса
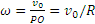
3) Определение ε. Так как величина PO=R остается постоянной при любом положении колеса, то
Знаки ω и ε совпадают, следовательно, вращение колеса ускоренное.
а) не следует думать, что если по условиям задачи 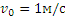
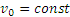
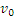
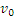
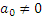
б) в данном случае 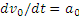
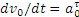
4) Определение 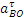
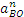
Учитывая, что в нашем случае BO=R, находим:
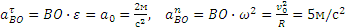
Показав на чертеже точку B отдельно, изображаем (без соблюдения масштаба) векторы, из которых слагается ускорение 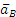
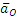
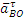
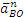
5) Вычисление 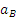
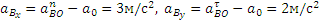
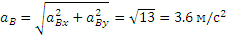
Аналогичным путем легко найти и ускорение точки P: 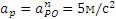
Задача 2.11.
Колесо катится по прямолинейному рельсу так, что скорость 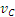
Решение.
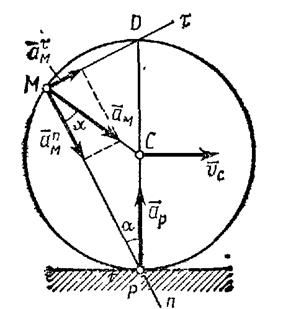 |
| Рис. 2.17. К задаче 2.11. |
Так как по условиям задачи 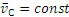
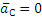
В результате ускорение точки М
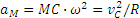
Таким образом, ускорение любой точки М обода (в том числе и точки Р) равно 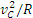
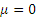
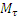
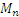
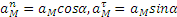
Зажача 2.12.
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна С, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами (рис.2.17 а). Точка D находится в середине стержня АВ. Длины стержней равны соответственно L1=0,4 м, L2 =1,2 м, L3=1,4 м, L4=0,6 м.
Дано: 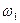
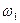
Найти: скорости точек В и C; угловую скорость 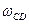
| а) | 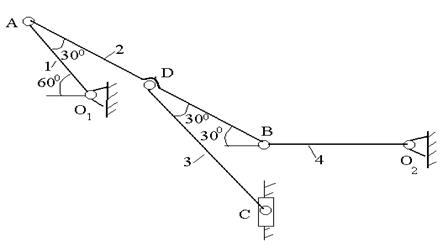 |
| б) | 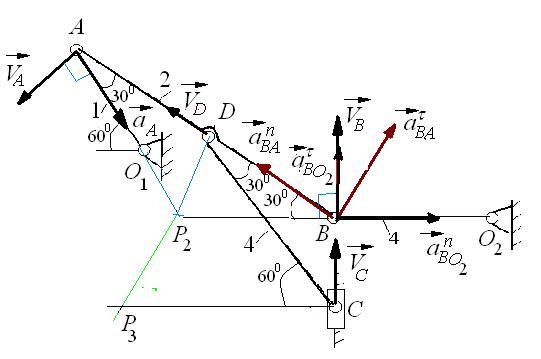 |
| Рис.2.17. К задаче 2.12. |
Решение (рис.2.12б)
1. Определим скорость точки А. Стержень OAвращается вокруг точко O1, поэтому скорость точки А определяется по формуле 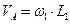
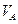
2. Определим угловую скорость стержня АВ. Точка В вращается вокруг центра О2, поэтому ее скорость перпендикулярна отрезку O2B. Для нахождения мгновенного центра скоростей отрезка АВ в точках А и В восстановим перпендикуляры к векторам 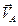
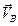
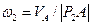
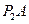
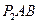
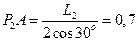
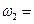
3. Определим скорость точки В по формуле 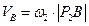
по формуле 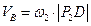
4. Определим скорость точки С. Так как точка С движется прямолинейно, то ее скорость направлена вдоль движения ползуна. Для нахождения мгновенного центра скоростей отрезка CD в точках C и D восстановим перпендикуляры к векторам 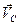
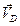
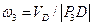
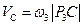
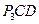
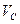
5. Определим угловую скорость отрезка О2В. Известно, что центром скоростей этого стержня является точка О2В , а также скорость точки B. Поэтому угловая скорость четвертого стержня вычисляется по формуле 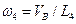
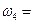
6. Определим ускорение точки А. Так как первый стержень вращается равномерно, то точка А имеет относительно О1 только нормальное ускорение, которое вычисляется по формуле 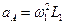
7. Определим ускорение точки В, которая принадлежит двум стержням — АВ и О2В. Поэтому ускорение точки В определяется с помощью двух формул
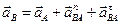
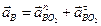
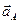
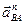
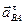
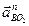
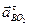
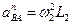
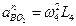
Можно составить уравнение
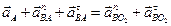
Решив полученную систему двух уравнений с двумя неизвестными, получим:
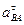
8. Определим угловое ускорение стержня АВ, используя формулу 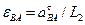
Задача 2.13.
Круглая пластина радиуса R=60 см вращается вокруг неподвижной оси по закону 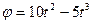
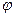
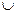
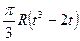
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t=1 с.
| а) | 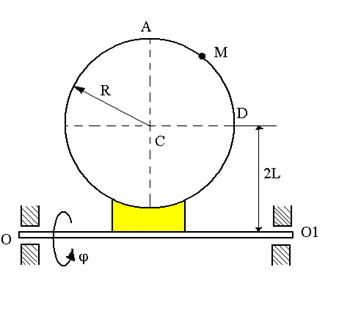 |
| б) | 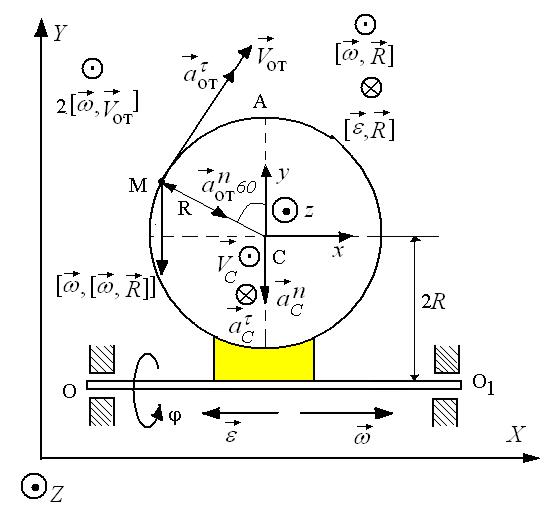 |
| Рис.2.18. К задаче 2.13. |
Решение (рис.2.13 б)
В качестве подвижной системы координат xyz примем точку С. Эта система совершает вращательное движение с угловой скоростью 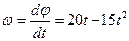
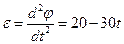
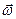
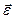
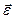
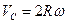
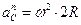
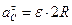
Вычислим путь, относительную скорость и ускорение точки M. Ее положение определяется величиной дуги S, в данный момент времени S = 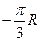
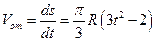
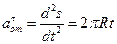
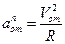
Абсолютная скорость точки M определяется по формуле
Где — 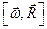
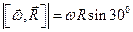
По теореме Пифагора 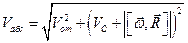
Абсолютное ускорение точки M определяется по формуле
Где 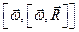
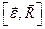
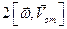
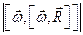
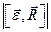
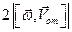
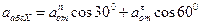
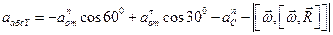
Теоретическая механика: Решебник Яблонского:
Кинематика твердого тела (К2, К3, К4, К5, К6)
Бесплатный онлайн решебник Яблонского. Выберите задание и номер варианта для просмотра решения. Смотрите также способы и примеры решения задач по теме вращательное движение твердого тела.
Видео:Физика - уравнения равноускоренного движенияСкачать

Задание К.2. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях
Движение груза 1 должно описываться уравнением
(1) x = c2t 2 + c1t + c0,
где t – время, с; с0-2 – некоторые постоянные.
В начальный момент времени (t=0) координата груза должна быть x0, а его скорость – v0.
Кроме того, необходимо, чтобы координата груза в момент времени t=t2 была равна x2.
Определить коэффициенты c0, c1 и c2, при которых осуществляется требуемое движение груза 1. Определить также в момент времени t=t1 скорость и ускорение груза и точки M одного из колес механизма.
Схемы механизмов показаны на рис. 68–70, а необходимые данные приведены в табл. 23.
Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)
Видео:Кинематика точки Задание К1Скачать

Задание К.3. Кинематический анализ плоского механизма
Найти для заданного положения механизма скорости и ускорения точек B и C, а также угловую скорость и угловое ускорение звена, которому эти точки принадлежат. Схемы механизмов помещены на рис. 73–75, а необходимые для расчета данные приведены в табл. 25.
Примечание. ωOA и εOA – угловая скорость и угловое ускорение кривошипа OA при заданном положении механизма; ω1 – угловая скорость колеса 1 (постоянная); vA и aA – скорость и ускорение точки A. Качение колес происходит без скольжения.
Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)
Видео:Теоретическая механика 2020 - Практика 1. Кинематика точки.Скачать

Задание К.4. Кинематический анализ многозвенного механизма
Кривошип O1A вращается с постоянной угловой скоростью ωO1A=2 рад/с. Определить для заданного положения механизма:
1) скорости точек A, B, C, . механизма и угловые скорости всех его звеньев с помощью плана скоростей;
2) скорости этих же точек механизма и угловые скорости звеньев с помощью мгновенных центров скоростей;
3) ускорения точек A и B и угловое ускорение звена AB;
4) положение мгновенного центра ускорений звена AB;
5) ускорение точки M, делящей звено AB пополам.
Схемы механизмов показаны на рис. 80–83, а необходимые для расчета данные приведены в табл. 27.
Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)
Видео:Решение графических задач на равномерное движениеСкачать

Задание К.5. Определение кинематических характеристик движения твердого тела и его точек по уравнениям Эйлера
Заданы уравнения сферического движения твердого тела ψ=ψ(t), θ=θ(t) и φ=φ(t), где ψ, θ и φ – углы Эйлера (рис. 90).
Определить для момента времени t=t1 угловую скорость и угловое ускорение тела, а также скорость и ускорение точки M, координаты которой в подвижной системе, жестко связанной с телом, ξ, η, ζ.
Необходимые данные приведены в табл. 32.
Варианты с решением: 3 5 11 14 19 20 23 28 (решено 27%)
Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Задание К.6. Кинематический анализ движения твердого тела, катящегося без скольжения по неподвижной поверхности и имеющего неподвижную точку
Тело A катится без скольжения по поверхности неподвижного тела B, имея неподвижную точку O. Ось Oζ тела A вращается вокруг неподвижной оси Oz и имеет при заданном положении тела A угловую скорость ω1 и угловое ускорение ε1.
Определить угловую скорость и угловое ускорение тела A, а также скорость и ускорение точки M в указанном положении тела А.
Схемы показаны на рис. 91–93, а необходимые для расчета данные приведены в табл. 33.
Примечание. Положительный и отрицательный знаки у ε1 означают соответственно, что вращение оси Oζ вокруг оси Oz происходит в направлении, показанном на схеме, ускоренно или замедленно.
🔍 Видео
Используя график скорости, составить уравнение движения тела, имеющего начальную координату -10 м.Скачать

Уравнение равномерного движения. Решение задач по теме.Скачать

Дифференциальное уравнение движения материальной точки.Скачать

Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Уравнение координат при равноускоренном движенииСкачать

Уравнение движения РУДСкачать

Равномерное прямолинейное движение - физика 9Скачать

Алгебра 7 класс. 26 октября. Составляем уравнение прямой проходящей через заданные точкиСкачать

Д1 Дифференциальные уравнения движения материальной точкиСкачать

Термех. Кинематика. Определение скорости и ускорения точек плоского механизма...Скачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать