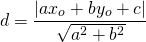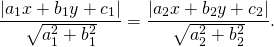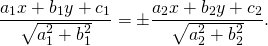Составить уравнение биссектрисы острого угла между прямыми x 7y 1 (4 видео)

Уравнение биссектрисы угла

Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.

Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0.

Расстояние от точки (x_o;y_o) до прямой ax+by+c=0 определяется по формуле

По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.

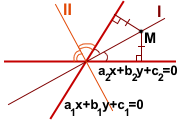
Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0, находится от этих прямых на одинаковом расстоянии, то есть

Это равенство можно записать в виде

Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.

Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.

В формулу уравнения биссектрис подставляем данные прямых:

Содержание

Составить уравнение биссектрисы острого угла между прямыми x 7y 1
Задача 34288 Составить уравнение биссектрисы угла.
Условие
Решение
📺 Видео

Видео:найти уравнения биссектрис углов между прямымиСкачать

Составить уравнение биссектрисы острого угла между прямыми x 7y 1

Найти уравнение биссектрис углов между прямыми 12x + 9y — 17 = 0 и 3x + 4y + 11 = 0.

Из элементарной геометрии известно, что биссектриса угла между двумя прямыми есть геометрическое место точек, равноудаленных от сторон угла. Обратимся к рисунку

Отклонения и точки A биссектрисы от сторон угла CDE имеют знак плюс, так как точка A и начало координат лежат по разные стороны как от первой, так и от второй прямой, т. е. . Возьмем точку B на биссектрисе смежного угла CDF. Точка B и начало координат лежат по разные стороны от прямой EF, поэтому отклонение имеет знак плюс ( > 0). Отклонение точки B от прямой CL имеет знак минус, так как точка B и начало координат лежат с одной и той же стороны от прямой CL, т. е. C₁ = 0 и A₂x + B₂y + C₂ = 0.

Видео:14. Угол между прямыми в пространствеСкачать

Задача 34288 Составить уравнение биссектрисы угла.

Условие

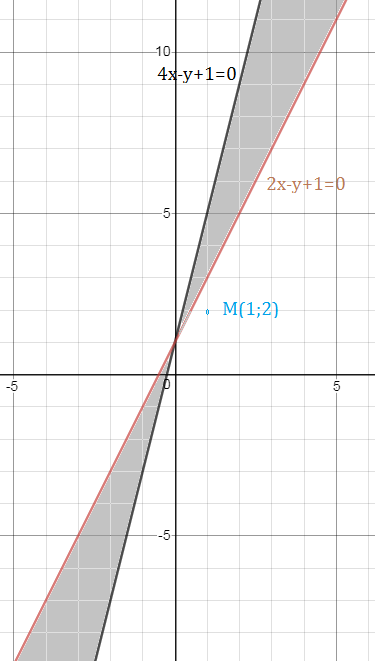
Составить уравнение биссектрисы угла между прямыми l1(4x–y+1=0) и l2(2x–y+1=0) смежного с углом, содержащим точку M(1;2)

Решение

Пусть точка Р(х;у) лежит на биссектрисе угла между прямыми.
Это значит, что расстояние d_(1) это точки до прямой l_(1) равно
расстоянию d_(2) это точки до прямой l_(2)

Прямая 4x–y+1=0 разбивает плоскость хОу на две области:
4x–y+1>0 или 4x–y+1 0 — верно;
Прямая 2x–y+1=0 разбивает плоскость хОу на две области:
2x–y+1>0 или 2x–y+1 0 — верно;

Значит точка M принадлежит области
4x–y+1>0
2x–y+1>0
а смежные области задаются неравенствами противоположных знаков.

Поэтому в (#) знак модуля раскрывается так:
(4x-y+1)/sqrt(4^2+1^2) =- (2x-y+1)/sqrt(2^2+1^2)

Делим на (sqrt(5)+sqrt(17))

((2sqrt(17)+4sqrt(5))/(sqrt(17)+sqrt(5))) * x — y + 1=0

Избавляемся от иррациональности в знаменателе

[b]((7 — sqrt(85))/6)*x — y + 1 = 0[/b]