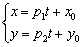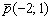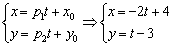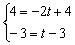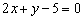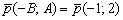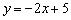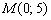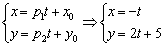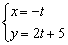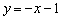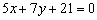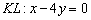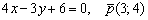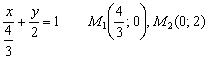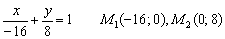Составить параметрическое уравнение прямой из общего уравнения (7 видео)

Параметрическое уравнение прямой на плоскости

В данной статье мы рассмотрим параметрическое уравнение прямой на плоскости. Приведем примеры построения параметрического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим методы преобразования уравнения в параметрическом виде в канонический и общий виды.

Параметрическое уравнение прямой L на плоскости представляется следующей формулой:

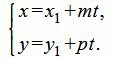Составить параметрическое уравнение прямой из общего уравнения

(1)

Отметим что при записи уравнения прямой в параметрическом виде, направляющий вектор прямой не должен быть нулевым вектором, т.е хотя бы один координат направляющего вектора q должен быть отличным от нуля.

Для построения прямой на плоскости в декартовой прямоугольной системе координат, заданной параметрическим уравнением (1), достаточно задать параметру t две разные значения, вычислить x и y и провести через эти точки прямую линию. При t=0 имеем точку M₁(x₁, y₁) при t=1, получим точку M₂(x₁+m, y₁+p).

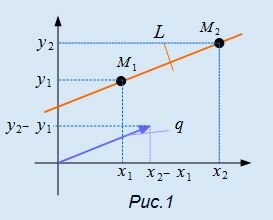
Для составления параметрического уравнения прямой на плоскости L достаточно иметь точку на прямой L и направляющий вектор прямой или две точки, принадлежащие прямой L. В первом случае, для построения параметрического уравнения прямой нужно координаты точки и направляющего вектора вставить в уравнение (1). Во втором случае сначала нужно найти направляющий вектор прямой q=<m, p>, вычисляя разности соответствующих координатов точек M₁ и M₂: m=x₂−x₁, p=y₂−y₁(Рис.1). Далее, аналогично первому случаю, подставить координаты одной из точек (не имеет значение какой именно) и направляющего вектора q прямой в (1).

Можно также вывести формулу параметрического уравнения прямой, проходящей через две точки. Для этого подставим значения m=x₂−x₁, p=y₂−y₁ в (1), получим параметрическое уравнение прямой на плоскости, проходящей через точки M₁(x₁, y₁) и M₂(x₂, y₂):

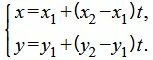(2)

Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q=. Построить параметрическое уравнение прямой.

Решение. Для построения параметрического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):

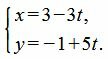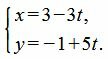Пример 2. Прямая проходит через точки M₁=(−5, 2) и M₂=(−2, 3). Построить параметрическое уравнение прямой.

Решение. Воспользуемся формулой (2). Подставим координаты точек M₁ и M₂ в уравнение (2):

Упростим полученное уравнение:

Содержание

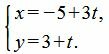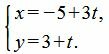Приведение параметрического уравнения на плоскости к каноническому виду
Приведение параметрического уравнения на плоскости к общему виду
Параметрические уравнения прямой на плоскости: описание, примеры, решение задач
Вывод параметрических уравнений прямой на плоскости
Составление параметрических уравнений прямой на плоскости
Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно
Примеры и задачи с параметрическими уравнениями прямой на плоскости
Как составить параметрические уравнениЯ прямой?
📹 Видео

Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Приведение параметрического уравнения на плоскости к каноническому виду

Выразим параметр t в (1) через переменные x и y:

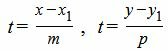(3)

Из выражений (3), можем записать каноническое уравнение прямой на плоскости:

(4)

Обратное преобразование смотрите здесь.

Пример 3. Прямая на плоскости представлена следующим параметрческим уравнением:

Привести данное уравнение прямой к каноническому виду.

Решение: Выразим параметр t через переменные x и y:

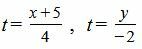(5)

Из выражений (5), можем записать:

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Приведение параметрического уравнения на плоскости к общему виду

Для приведения параметрического уравнения прямой на плоскости к общему виду, в формулах (1) выразим из второго уравнения параметр t через переменную y и подставим в первое уравнение:

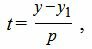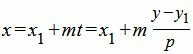(6)

Умножим обе части уравнения (6) на p и группируем элементы уравнения:

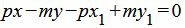(7)

Сделаем обозначения: A=p, B=−m, C=−px₁+my₁. Тогда получим общее уравнение прямой:

Обратное преобразование смотрите здесь.

Пример 4. Прямая на плоскости представлена следующим параметрческим уравнением:

(9)

Привести данное уравнение прямой к общему виду.

Решение: В уравнении (9) имеем: x₁=−5, y₁=0, m=4, p=−2. Подставим эти значения в формулу (7):

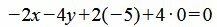(10)

Упростив выражение (10) получим общее уравнение прямой (9):

Видео:Параметрические уравнения прямойСкачать

Параметрические уравнения прямой на плоскости: описание, примеры, решение задач

Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.

Видео:11. Прямая в пространстве и ее уравненияСкачать

Вывод параметрических уравнений прямой на плоскости

Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.

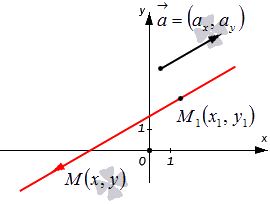
Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 ( x 1 , y 1 ) и направляющий вектор заданной прямой a → = ( a x , a y ) . Дадим описание заданной прямой a , используя уравнения.

Используем произвольную точку М ( x , y ) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = ( x — x 1 , y — y 1 ) . Опишем полученное: прямая задана множеством точек М ( x , y ) , проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) являются коллинеарными.

Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) возможно записать в виде уравнения:

M 1 M → = λ · a → , где λ – некоторое действительное число.

Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.

В координатной форме оно имеет вид:

M 1 M → = λ · a → ⇔ x — x 1 = λ · a x y — y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ

Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ

Видео:Видеоурок "Канонические уравнения прямой"Скачать

Составление параметрических уравнений прямой на плоскости

Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.

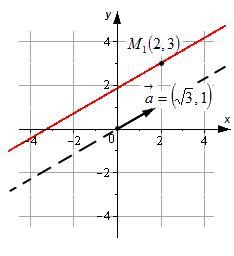
Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 ( 2 , 3 ) и ее направляющий вектор a → = ( 3 , 1 ) .

Решение

На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ

Ответ: x = 2 + 3 · λ y = 3 + λ

Необходимо отметить: если вектор a → = ( a x , a y ) служит направляющим вектором прямой а, а точки М 1 ( x 1 , y 1 ) и М 2 ( x 2 , y 2 ) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .

К примеру, нам заданы направляющий вектор прямой a → = ( 2 , — 1 ) , а также точки М 1 ( 1 , — 2 ) и М 2 ( 3 , — 3 ) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = — 2 — λ или x = 3 + 2 · λ y = — 3 — λ .

Следует обратить внимание и на такой факт: если a → = ( a x , a y ) — направляющий вектор прямой a , то ее направляющим вектором будет и любой из векторов μ · a → = ( μ · a x , μ · a y ) , где μ ϵ R , μ ≠ 0 .

Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.

Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = — 2 — 5 · λ . Тогда a → = ( 2 , — 5 ) — направляющий вектор этой прямой. А также любой из векторов μ · a → = ( μ · 2 , μ · — 5 ) = 2 μ , — 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор — 2 · a → = ( — 4 , 10 ) , ему соответствует значение μ = — 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 — 4 · λ y = — 2 + 10 · λ .

Видео:Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно

В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.

Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x — x 1 a x = y — y 1 a y .

Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y

При этом не должно смущать, если a x или a y будут равны нулю.

Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = — 2 — 4 · λ к каноническому уравнению.

Решение

Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = — 2 — 4 · λ

Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = — 2 — 4 · λ ⇔ λ = x — 3 0 λ = y + 2 — 4

Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:

x — 3 0 = y + 2 — 4

Ответ: x — 3 0 = y + 2 — 4

В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y ⇔ ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ A x + B y + C = 0

Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = — 1 + 2 · λ y = — 3 · λ

Решение

Для начала осуществим переход к каноническому уравнению:

x = — 1 + 2 · λ y = — 3 · λ ⇔ λ = x + 1 2 λ = y — 3 ⇔ x + 1 2 = y — 3

Полученная пропорция идентична равенству — 3 · ( x + 1 ) = 2 · y . Раскроем скобки и получим общее уравнение прямой: — 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .

Ответ: 3 x + 2 y + 3 = 0

Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.

Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.

Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x — x 1 a x = y — y 1 a y . Каждое из отношений этого равенства примем равным параметру λ :

x — x 1 a x = y — y 1 a y = λ ⇔ λ = x — x 1 a x λ = y — y 1 a y

Разрешим полученные уравнения относительно переменных x и y :

x = x 1 + a x · λ y = y 1 + a y · λ

Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x — 2 5 = y — 2 2

Решение

Приравняем части известного уравнения к параметру λ : x — 2 5 = y — 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x — 2 5 = y — 2 2 = λ ⇔ λ = x — 2 5 λ = y — 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ

Ответ: x = 2 + 5 · λ y = 2 + 2 · λ

Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.

Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x — 3 y — 3 = 0 .

Решение

Заданное общее уравнение преобразуем в уравнение канонического вида:

4 x — 3 y — 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4

Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:

x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = — 1 3 + 4 · λ

Ответ: x = 3 · λ y = — 1 3 + 4 · λ

Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Примеры и задачи с параметрическими уравнениями прямой на плоскости

Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.

В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.

Решение таких задач опирается на следующий факт: числа ( x , y ) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.

Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 — 1 6 · λ y = — 1 + 2 · λ при λ = 3 .

Решение

Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 — 1 6 · 3 y = — 1 + 2 · 3 ⇔ x = 1 1 2 y = 5

Ответ: 1 1 2 , 5

Также возможна следующая задача: пусть задана некоторая точка M 0 ( x 0 , y 0 ) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .

Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.

Заданы точки М 0 ( 4 , — 2 ) и N 0 ( — 2 , 1 ) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = — 1 — 1 2 · λ .

Решение

Подставим координаты точки М 0 ( 4 , — 2 ) в заданные параметрические уравнения:

4 = 2 · λ — 2 = — 1 — 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2

Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .

Далее по аналогии проверим заданную точку N 0 ( — 2 , 1 ) , подставив ее координаты в заданные параметрические уравнения:

— 2 = 2 · λ 1 = — 1 — 1 2 · λ ⇔ λ = — 1 λ = — 4

Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 ( — 2 , 1 ) .

Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.

В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.

Пример 8

Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y — 3 — 1 .

Решение

По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y — 3 — 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y — 3 — 1 , который запишем в виде: a → = ( 2 , — 1 ) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + ( — 1 ) · λ ⇔ x = 1 2 + x · λ y = 2 3 — λ

Ответ: x = 1 2 + x · λ y = 2 3 — λ .

Задана точка М 1 ( 0 , — 7 ) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .

Решение

В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты ( 3 , — 2 ) . Запишем требуемые параметрические уравнения прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = — 7 + ( — 2 ) · λ ⇔ x = 3 · λ y = — 7 — 2 · λ

Ответ: x = 3 · λ y = — 7 — 2 · λ

В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.

Пример 10

Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 — 3 4 · λ y = — 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.

Решение

Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:

x = 1 — 3 4 · λ y = — 1 + λ ⇔ λ = x — 1 — 3 4 λ = y + 1 1 ⇔ x — 1 — 3 4 = y + 1 1 ⇔ ⇔ 1 · x — 1 = — 3 4 · y + 1 ⇔ x + 3 4 y — 1 4 = 0

Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 — 3 4 · λ y = — 1 + λ имеет координаты 1 , 3 4 .

Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Как составить параметрические уравнениЯ прямой?

Параметрические уравнения прямой больше актуальны для прямых в пространстве, но без них наш конспект осиротеет.

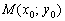
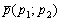
Если известна некоторая точка , принадлежащая прямой, и направляющий вектор этой прямой, то параметрические уравнения данной прямой задаются системой:

Что такое функция, заданная параметрически, я уже объяснял в статье Производная неявной и параметрически заданной функций. Но всё равно немного повторюсь в следующей демонстрационной задаче:

Составить параметрические уравнения прямой по точке 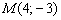и направляющему вектору

Решение закончилось, не успев начаться:

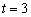
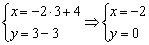
Параметр «тэ» может принимать любые значения от «минус бесконечности» до «плюс бесконечности», и каждому значению параметра соответствует конкретная точка плоскости. Например, если , то получаем точку .

Обратная задача: как проверить, будет ли точка 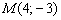условия принадлежать данной прямой?

Подставим координаты точки 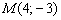в полученные параметрические уравнения:

Из обоих уравнений следует, что 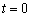, то есть, система совместна и имеет единственное решение.

Рассмотрим более содержательные задания:

Составить параметрические уравнения прямой

Решение: По условию прямая задана в общем виде. Для того чтобы составить параметрические уравнения прямой, нужно знать её направляющий вектор и какую-нибудь точку, принадлежащую данной прямой.

Найдём направляющий вектор:

Теперь нужно найти какую-нибудь точку, принадлежащую прямой (подойдёт любая), в этих целях общее уравнение удобно переписать в виде уравнения с угловым коэффициентом:

Напрашивается, конечно, точка

Составим параметрические уравнения прямой:

Ответ:

И напоследок небольшая творческая задача для самостоятельного решения.

Составить параметрические уравнения прямой, если известна принадлежащая ей точка 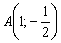и вектор нормали

Задачу можно оформить не единственным способом. Одна из версий решения и ответ в конце урока.

Существуют другие, более экзотические способы задать прямую, но то, что уже рассмотрено, хватит за глаза и за уши. Следующая статья, которую я рекомендую, называетсяПростейшие задачи с прямой на плоскости. В ней рассматриваются вещи, которые позволят окончательно укрепить ваш геометрический фундамент.

Решения и ответы:

Пример 2: Решение: Найдём угловой коэффициент:

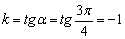
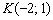
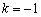
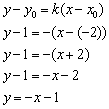
Уравнение прямой составим по точке и угловому коэффициенту :

Ответ:

Пример 4: Решение: Уравнение прямой составим по формуле:

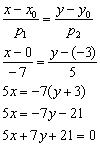
Ответ:

Пример 6: Решение: Используем формулу:

Ответ: 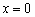(ось ординат)

Пример 8: Решение: Составим уравнение прямой по двум точкам:

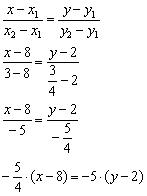
Умножаем обе части на –4:

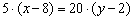
И делим на 5:

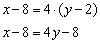
Ответ:

Пример 10: Решение: Используем формулу:

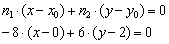
Сокращаем на –2:

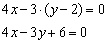
Направляющий вектор прямой: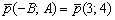
Ответ:

Пример 12:
а)Решение: Преобразуем уравнение:

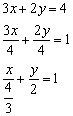
Таким образом:

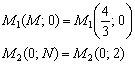
Ответ:

б)Решение: Преобразуем уравнение:

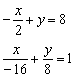
Таким образом:

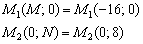
Ответ:

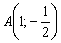
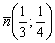
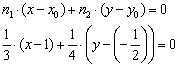
Пример 15: Решение: Сначала составим общее уравнение прямой по точке и вектору нормали :

Умножаем на 12:

Умножаем ещё на 2, чтобы после раскрытия второй скобки избавиться от дроби:

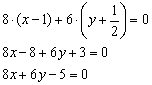
Направляющий вектор прямой: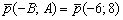
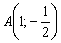
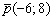
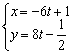
Параметрические уравнения прямой составим по точке и направляющему вектору :
Ответ:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Простейшие задачи с прямой на плоскости.
Взаимное расположение прямых. Угол между прямыми

Продолжаем рассматривать эти бесконечные-бесконечные прямые. На уроке Уравнение прямой на плоскости мы познакомились с основными видами уравнений, направляющим вектором прямой и её вектором нормали. Данная статья является логическим продолжением темы, и в ней будут разобраны следующие типовые задачи:

Как определить взаимное расположение двух прямых? Как построить прямую, параллельную данной? Как найти точку пересечения двух прямых? Как построить прямую, перпендикулярную данной? Как найти расстояние от точки до прямой? Как построить точку, симметричную относительно прямой? Как найти расстояние между двумя параллельными прямыми? Как найти угол между двумя прямыми?

О-о-о-о-о… ну и жесть, словно сам себе приговор зачитал =) Впрочем, потом релаксация поможет, тем более, сегодня купил подходящие аксессуары. Поэтому приступим к первому разделу, надеюсь, к концу статьи сохраню бодрое расположение духа.