1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Вычисляем высоту через координаты вершин 1Скачать  Составить каноническое уравнение высоты пирамиды проведенной из вершиныВнимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут Неправильный логин или пароль. Укажите электронный адрес и пароль. Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем. Инструкция по изменению пароля отправлена на почту. Чтобы зарегистрироваться, укажите ваш email и пароль Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности. Видео:Уравнения стороны треугольника и медианыСкачать  Уравнения прямой в пространствеПараметрические уравнения прямой l в пространстве: где t – числовой параметр. Каждому значению параметра Канонические уравнения прямой: Уравнения прямой, проходящей через две данные точки Углом Углом между плоскостью и прямой l (в случае их пересечения) называется угол между прямой и её проекцией на плоскость. Синус угла Примерный вариант и образец выполнения РГЗ №1 Задача 1. Даны координаты вершин треугольника АВС: Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. Задача 2.Даны координаты точек – вершин пирамиды ABCD: 1) вычислить длину ребра AB; 2) найти уравнение плоскости грани ABC; 3) найти угол 4) составить параметрические уравнения прямой AB; 5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7) найти угол 8) найти угол 9) сделать чертеж пирамиды в системе координат. Решение задачи 1. 1) Вычислим длину стороны ВС по формуле (1): |BС|= 2) Составим уравнение стороны ВС, используя формулу (8): 3) Внутренний угол треугольника при вершине В найдем как угол между прямыми ВА и ВС. Для этого сначала вычислим угловой коэффициент прямой ВА по формуле (7): и возьмем из уравнения ВС угловой коэффициент прямой ВС: Из расположения точек A, B, C на координатной плоскости видно, что угол В в треугольнике ABC – острый, поэтому по формуле (11) вычислим 4) Для получения уравнения высоты АK, проведенной из вершины А, используем уравнение пучка прямых (6) и условие перпендикулярности прямых (10). Сначала вычислим угловой коэффициент прямой АK . Так как Уравнение AK получим по формуле (6): у – уА = kAK(x– xA) 5) Для определения координат центра тяжести треугольника используем свойство точки пересечения его медиан: если AМ – медиана треугольника и P – точка пересечения его медиан, то P делит AМ в отношении 2 : 1, начиная от точки А, т.е. Основание медианы AМ – точка М является серединой отрезка ВС. Найдем координаты точки М по формулам (3): Теперь, когда координаты концов отрезка AМ известны, найдем координаты точки P, которая делит AМ в отношении P(3; 1) – центр тяжести треугольника АВС. 6) Построим чертеж к задаче в системе координат ХОY (рис. 3). Полученные при решении задачи результаты не противоречат чертежу. 1) длина стороны |BС| = 2) уравнение стороны ВС: y = –2x + 14; 3) угол при вершине В: 4) уравнение высоты АK: x –2y + 1 = 0; 5) координаты центра тяжести треугольника P(3; 1); 6) чертеж на рис. 3. Решение задачи 2. 1) Длину ребра 2) Чтобы получить уравнение плоскости грани ABC, необходимо найти вектор, перпендикулярный плоскости ABC, т.е. вектор, перпендикулярный векторам Найдем векторное произведение 3) Прежде, чем найти угол Из уравнения плоскости BCD возьмем координаты вектора нормали Косинус угла Отсюда 4) Уравнения ребра AB можно записать как параметрические уравнения прямой, проходящей через точку A(–2;1;1) и имеющей направляющий вектор Другой способ: можно использовать уравнения прямой, проходящей через две точки откуда, обозначив каждую из дробей буквой t, получаем: 5) Высота пирамиды DK – это прямая, проведенная из вершины D перпендикулярно грани ABC. Она имеет направляющий вектор 6) Прежде, чем найти точку пересечения DK и грани ABC, получим параметрические уравнения прямой DK.Обозначив каждую из дробей в канонических уравнениях буквой t, получаем: Точка пересечения DK и грани ABC (точка К) лежит на прямой, а значит, имеет координаты Решим последнее уравнение относительно t: Вычислим координаты точки K, подставив найденное значениепараметра t в первые три уравнения системы: Итак, точка пересечения DK и грани ABC: 7) Угол Тогда угол между ребрами AB и BC: 8) Чтобы определить угол Тогда угол между ребром AD и гранью ABC: 9) Выполним чертеж пирамиды в системе координат (рис.4). 1) 2) АВС: 3) 4) 5) DK: 7) 💥 ВидеоДаны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать  Вычисление медианы, высоты и угла по координатам вершинСкачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  Математика без Ху!ни. Уравнение плоскости.Скачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Математика без Ху!ни. Смешанное произведение векторовСкачать  Написать канонические и параметрические уравнения прямой в пространствеСкачать  Видеоурок "Канонические уравнения прямой"Скачать  Даны координаты вершин треугольника АВС.Скачать  Уравнение прямой и треугольник. Задача про высотуСкачать  №973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать  Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать  Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать  найти уравнение высоты треугольникаСкачать  Каноническое уравнение окружностиСкачать  Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать  Построение проекции пирамиды. Метод прямого треугольника.Скачать  | |
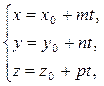 (15)
(15)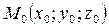 – фиксированная точка прямой;
– фиксированная точка прямой;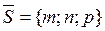 – направляющий вектор прямой l, т.е. любой вектор, параллельный l;
– направляющий вектор прямой l, т.е. любой вектор, параллельный l;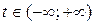 соответствует единственная точка прямой l.
соответствует единственная точка прямой l.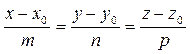 . (16)
. (16)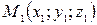 и
и 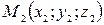 :
: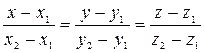 . (17)
. (17)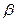 между прямыми называют угол между их направляющими векторами
между прямыми называют угол между их направляющими векторами 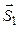 =<m1; n1; p1> и
=<m1; n1; p1> и 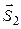 =<m2; n2; p2>, или дополнительный к нему (обычно берется острый угол), то есть
=<m2; n2; p2>, или дополнительный к нему (обычно берется острый угол), то есть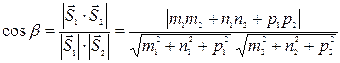 . (18)
. (18)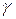 между плоскостью
между плоскостью  и прямой
и прямой 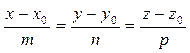 определяется по формуле:
определяется по формуле: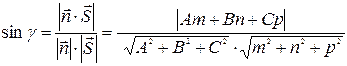 . (19)
. (19)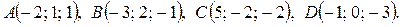
 между гранями ABC и BCD;
между гранями ABC и BCD; между ребрами AB и BC;
между ребрами AB и BC;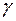 между ребром AD и гранью ABC;
между ребром AD и гранью ABC;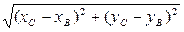 =
= 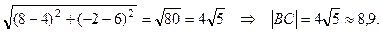
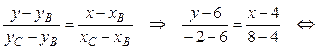
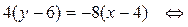
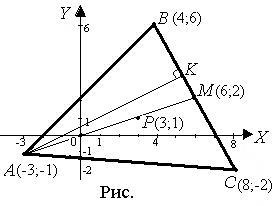
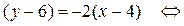 y = –2x + 14 – уравнение ВС.
y = –2x + 14 – уравнение ВС.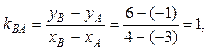
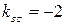 .
.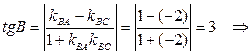
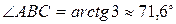 .
.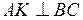 , то
, то 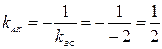 .
.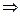 у – (–1) =
у – (–1) = 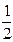 (x– (–3))
(x– (–3)) 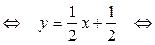
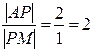 .
.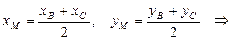
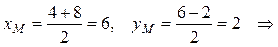 М(6; 2).
М(6; 2).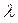 = 2, начиная от точки А, по формулам деления отрезка в заданном отношении (2):
= 2, начиная от точки А, по формулам деления отрезка в заданном отношении (2):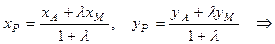
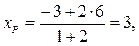
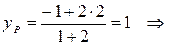
 ;
;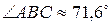 ;
;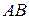 найдем по формуле:
найдем по формуле: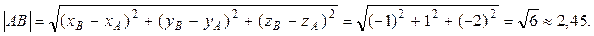
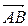 и
и 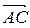 . Одним из таких векторов является векторное произведение
. Одним из таких векторов является векторное произведение 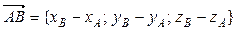 = = ,
= = ,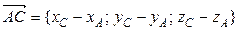 =.
=.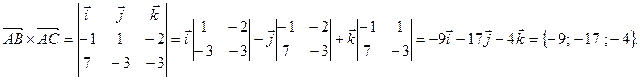 В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например,
В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например, 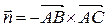 = . Используем уравнение плоскости, проходящей через точку
= . Используем уравнение плоскости, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору 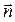 (формула (12):
(формула (12): 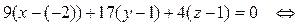
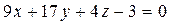 – уравнение плоскости грани ABC.
– уравнение плоскости грани ABC.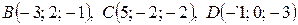 (формула (13):
(формула (13):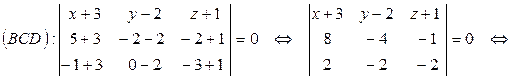
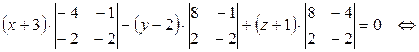
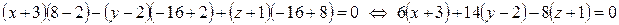
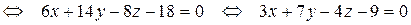 – уравнение грани BCD.
– уравнение грани BCD.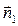 , перпендикулярного этой плоскости:
, перпендикулярного этой плоскости: 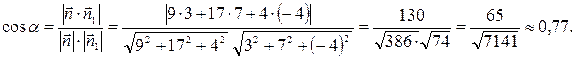
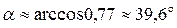 .
. = (формулы (15)):
= (формулы (15)):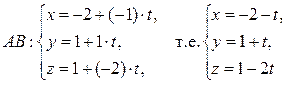 – параметрические уравнения AB.
– параметрические уравнения AB.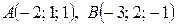 (формулы (17)):
(формулы (17)):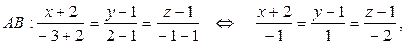
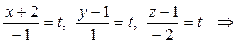
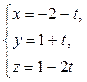 – параметрические уравнения AB.
– параметрические уравнения AB.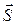 , коллинеарный вектору нормали плоскости ABC. Можно взять, например,
, коллинеарный вектору нормали плоскости ABC. Можно взять, например, 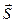 =
= 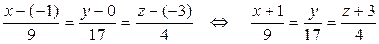 – канонические уравнения DK.
– канонические уравнения DK.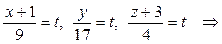
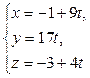 – параметрические уравнения DK.
– параметрические уравнения DK.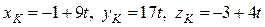 , и принадлежит плоскости, т.е. ее координаты удовлетворяют уравнению плоскости ABC. Поэтому координаты точки K найдем, решив систему:
, и принадлежит плоскости, т.е. ее координаты удовлетворяют уравнению плоскости ABC. Поэтому координаты точки K найдем, решив систему: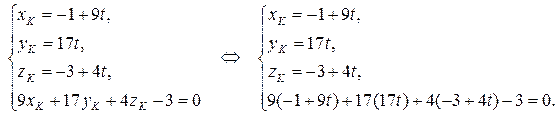
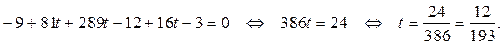
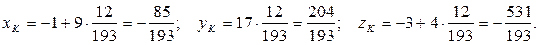

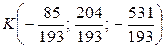 .
.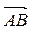 = и
= и 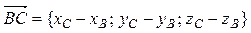 =. Вычислим косинус угла
=. Вычислим косинус угла 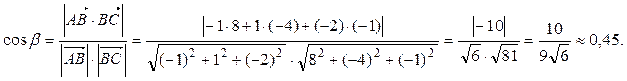
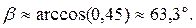
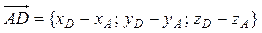 =. Плоскость ABC имеет вектор нормали
=. Плоскость ABC имеет вектор нормали 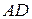 и плоскостью ABC можно вычислить по формуле (19):
и плоскостью ABC можно вычислить по формуле (19):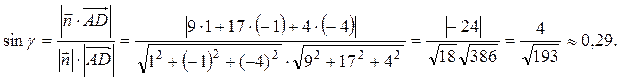

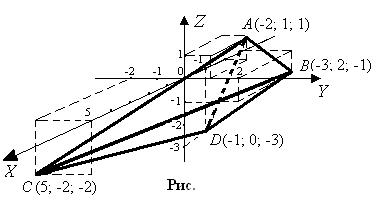
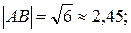
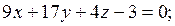
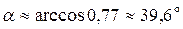 ;
;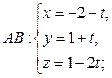
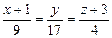 ; 6)
; 6) 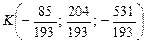 ;
;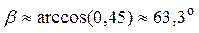 ; 8)
; 8) 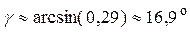 ;
;