Составить каноническое уравнение гиперболы 9х2 16у2 144 найти координаты фокусов вершин

Условие

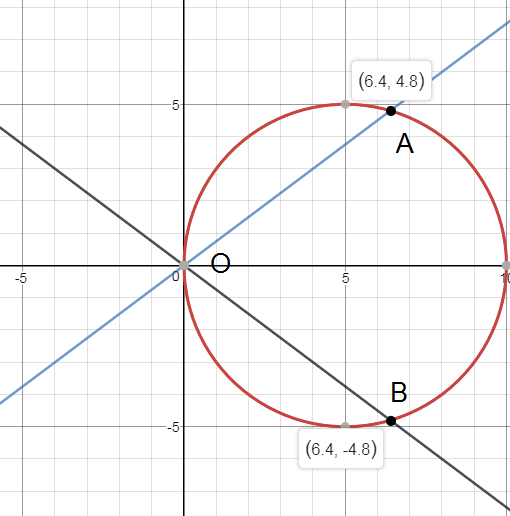
4.3.81) Найти расстояние между точками пересечения асимптот гиперболы
9х^2-16у^2 = 144 с окружностью, имеющей центр в правом фокусе гиперболы и проходящей через начало координат.

Решение

Канонический вид гиперболы:
(x^2/a^2)-(y^2/b^2)=1

[b] Уравнения асимптот гиперболы имеют вид:[/b]

[b]Фокусы гиперболы имеют координаты
F_(1)(-с;0) и F_(2)(с;0)
b^2=c^2-a^2[/b]

Разделим обе части уравнения на 144:
(9x^2/144)-(16у^2/144)=1
Канонический вид гиперболы:
(x^2/16)-(y^2/9)=1
a^2=16
b^2=9
Тогда
[b] уравнения асимптот гиперболы

c^2=b^2+a^2=9+16=25
[b]Фокусы гиперболы имеют координаты
F_(1)(-5;0) и F_(2)(5;0) [/b]

Уравнение окружности с центром в точке
F_(2) (5;0) и радиусом R=5 имеет вид

Чтобы найти точки пересечения гиперболы
асимптоты y=(-3/4)x
и
окружности
(x-5)^2+y^2=25
решим систему уравнений:

Подставим y=(-3/4)x во второе уравнение
(х-5)^2+((-3/4)x)^2 = 25;

Итак, асимптота y=(-3/4)x пересекается с окружностью
(х-5)^2+y^2=25 в точках
O(0;0) и А(6,4; — 4,8)
Аналогично, асимптота y=(3/4)x пересекается с окружностью (х-5)^2+y^2=25 в точках
O(0;0) и B(6,4; + 4,8)

О т в е т. 8; 9,6

Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

На гиперболе 9х² — 16у² = 144 найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого?

Математика | 10 — 11 классы

На гиперболе 9х² — 16у² = 144 найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого.

Каноническое уравнение гиперболы

Очевидно, что для нашего случая

Фокусное расстояние находим из соотношения

Теперь осталось найти точки, расстояние от которых до (5 ; 0) в два раза больше, чем до ( — 5 ; 0)

Второе решение не подходит, т.

К. квадрат y не может быть отрицательным

Таким образом решением являются две точки :

Видео:Видеоурок "Гипербола"Скачать

Назови три числа, изображения которых на координатном луче находятся : а) правее точки A (25) б) левее точки B (118) в) правее точки C(2), но левее точки D (15) г) правеее точки E(7), но левее точки F?

Назови три числа, изображения которых на координатном луче находятся : а) правее точки A (25) б) левее точки B (118) в) правее точки C(2), но левее точки D (15) г) правеее точки E(7), но левее точки F(8) (спасибо вам заранее, а то я не понила) ^ _ ^.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Составить уравнение линии, для каждой точки которой расстояние до точки А (0 ; 1) вдвое меньше расстояния до прямой y = 4 ?

Составить уравнение линии, для каждой точки которой расстояние до точки А (0 ; 1) вдвое меньше расстояния до прямой y = 4 .

Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Запишите координаты всех точек, которые на координатной прямой расположены : а) левее точки с координатой 15 б) левее точки с координатой 27, но правее точки с координатой 12?

Запишите координаты всех точек, которые на координатной прямой расположены : а) левее точки с координатой 15 б) левее точки с координатой 27, но правее точки с координатой 12.

Видео:§21 Каноническое уравнение гиперболыСкачать

Запишите координаты всех точек, которые на координатной прямой расположены?

Запишите координаты всех точек, которые на координатной прямой расположены.

А) левее точки с координатой 15

б) левее точки с координатой 27, но правее точки с координатой 12.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Сколько имеется точек с натуральными координатами, которые на координатной прямой расположены а)левее точки А(15) б) правее точки В(10) в) правее точки С (12), но левее точки D(22)?

Сколько имеется точек с натуральными координатами, которые на координатной прямой расположены а)левее точки А(15) б) правее точки В(10) в) правее точки С (12), но левее точки D(22).

Видео:§29 Эксцентриситет гиперболыСкачать

Определить уравнение траектории точки M(x?

Определить уравнение траектории точки M(x.

Y), которая движется так, что ее расстояние от точки F( — 1.

0) остается вдвое меньше расстояния от прямой x = — 4.

Видео:213. Фокус и директриса параболы.Скачать

Составить простейшие уравнение гиперболы если расстояние между ее вершинами равна 20 а расcтояние между фокусами 30?

Составить простейшие уравнение гиперболы если расстояние между ее вершинами равна 20 а расcтояние между фокусами 30.

Видео:§23 Построение гиперболыСкачать

Даны координаты фокусов гиперболы — F1(4 ; 2) , F2( — 1 ; — 10) и уравнение касательной 3х + 4у — 5 = 0?

Даны координаты фокусов гиперболы — F1(4 ; 2) , F2( — 1 ; — 10) и уравнение касательной 3х + 4у — 5 = 0.

Найти параметр а гиперболы.

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Составить каноническое уравнение параболы с вершиной в начале координат, симметричной ОУ , фокус которой в точке F(0 ; — 3) Составить уравнение эллипса , проходящего через точку А(4 ; 6) , фокусы кото?

Составить каноническое уравнение параболы с вершиной в начале координат, симметричной ОУ , фокус которой в точке F(0 ; — 3) Составить уравнение эллипса , проходящего через точку А(4 ; 6) , фокусы которого совпадают с фокусами гиперболы x ^ 2 — y ^ 2 = 8.

Видео:Каноническое уравнение окружностиСкачать

Найти уравнение параболы, вершины которой находится в точке (3 ; 2) и фокус в точке (5 ; 2)?

Найти уравнение параболы, вершины которой находится в точке (3 ; 2) и фокус в точке (5 ; 2).

Вы перешли к вопросу На гиперболе 9х² — 16у² = 144 найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого?. Он относится к категории Математика, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Выражение — это какой — либо пример. Например, 2 + 3 А значение выражения — это ответ, получившийся в примере 2 + 3 = 5.

(x — 2) = 0 / 0, 8 ; x — 2 = 0 ; x = 2. Ответ : x = 2.

20 = 2×2×5 30 = 2×3×5 Одинаковые числа 2 ; 5 НОД (20 ; 30) = 2×5 = 10.

В школу пришло всего 248 детей.

19, 21 — 2, 3 = 17, 21 — 0, 3 = 16, 91 51, 64 — 9, 16 = 45, 48 УДачи! Отметь моё решение как лучшее плиз.

19, 21 — 2, 3 = 16, 91 51, 64 — 9, 16 = 42. 48.

25 / 44 * 3 = 75 / 132 25 / 44 * 5 = 125 / 220 25 / 44 * 9 = 225 / 396 25 / 44 * 11 = 275 / 484.

Вот))))))) Удачи в дальнейшем ))))))))(.

1) (12)² = 144 2) (а + в)(а — в) = а² — в² = 49 — 25 = 24 3) (2)(2)(2) = 8 4) а² + 2ав + в² = (а + в)² = 144 5)а² — в² = 24 Удачи.

Дубы 25%, дубы и клены 25 + 30 = 55% берез 100 — 55 = 45% берез больше кленов на 45 — 30 = 15% пропорция 15% — 120 45% — х х = 45 * 120 / 15 = 3 * 120 = 360 берез в парке вычисления проверь.

Видео:Фокусы гиперболыСкачать

2.4 Гипербола

Гиперболой Называется геометрическое место точек на плоскости, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная.

Обозначим эту постоянную через 2А, расстояние между фокусами через 2С, а оси координат выберем так же, как в разделе 2.3.

Пусть М(Х, У) – произвольная точка гиперболы (рисунок 2.4).

По определению гиперболы F2M – F1М = ±2A. (Знак плюс в правой части надо выбрать, если F2M > F1М, и минус, если F2M A).

Исследуем формулу гиперболы.

1. Уравнение (2.7) содержит квадраты текущих координат, следовательно, оси координат являются осями симметрии гиперболы. Ось симметрии, на которой находятся фокусы, называется фокальной осью, точка пересечения осей симметрии – центром гиперболы. Для гиперболы, заданной уравнением (2.7), фокальная ось совпадает с осью ОХ, а центр – с началом координат.

В этом случае координаты фокусов гиперболы имеют вид F1(с,0), F2(-с,0).

2. Точки пересечения с осями симметрии. Точки пересечения гиперболы с осями симметрии называются Вершинами гиперболы. Полагая в уравнении (2.7) У = 0, найдем абсциссы точек пересечения с осью ОХ:

или X2 = А2, откуда Х = ±А.

Итак, точки и являются вершинами гиперболы.

Если же в уравнении (2.7) принять x = 0, получим

или У2 = –B2,

Т. е. для У мы получили мнимые значения. Это означает, что гипербола не пересекает ось ОY.
В соответствии с этим ось симметрии, пересекающая гиперболу, называется действительной осью (фокальная ось); ось симметрии, которая не пересекает гиперболу, – ее мнимой осью. Для гиперболы, заданной уравнением (2.7), действительной осью симметрии является ось ОХ, а мнимой осью – ось ОY. Длина отрезка А1А2 = 2А, число А называется действительной полуосью гиперболы. Отложим на мнимой оси гиперболы по обе стороны от центра симметрии O отрезки ОВ1 и ОВ2 длиною B, тогда отрезок В1B2 = 2B называют мнимой осью, а величину B – мнимой полуосью гиперболы.

Из уравнения (2.7) видно, что , следовательно, |X| ³ A. Кривая имеет форму, изображенную на рисунке 2.5. Она располагается вне прямоугольника со сторонами, равными 2А и 2B, с центром в начале координат, и состоит из двух отдельных ветвей, простирающихся в бесконечность (см. рисунок 2.5). Диагонали этого прямоугольника определяются уравнениями

(2.8)

И являются Асимптотами гиперболы.

Если A = B, гипербола называется равносторонней.

Замечание 1. Если мнимая ось гиперболы равна 2А и расположена на оси ОХ, а действи-тельная ось равна 2B и расположена на оси ОY, то уравнение такой гиперболы (рисунок 2.6) имеет вид (каноническое уравнение гиперболы, если ее фокальная ось – ось Y)

(2.9)

Координаты фокусов в этом случае имеет вид F1(0,с) и F2(0,-с).

Гиперболы (2.7) и (2.9) называются Сопряженными гиперболами.

Замечание 2. Эксцентриситетом Гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы

(2.10)

Для любой гиперболы ε > 1, это число определяет форму гиперболы.

Пример 2.3. Найти координаты фокусов и вершин гиперболы

Написать уравнение ее асимптот и вычислить эксцентриситет.

Решение. Напишем каноническое уравнение гиперболы, для чего обе части уравнения поделим на 144. После сокращения получим

.

Отсюда видно, что А2 = 9, т. е. A = 3 и B2 = 16, т. е. B = 4.

Для гиперболы С2 = А2 + B2 = 16 + 9 = 25, отсюда C = 5.

Теперь можем написать координаты вершин и фокусов гиперболы:

Эксцентриситет , а уравнения асимптот имеют вид

и .

🔍 Видео

§24 Каноническое уравнение параболыСкачать

§18 Каноническое уравнение эллипсаСкачать

Как легко составить уравнение параболы из графикаСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

Кривые второго порядка. Гипербола. Приведение к каноническому виду и чертежСкачать

Парабола (часть 1). Каноническое уравнение параболы. Высшая математика.Скачать

Неполное уравнение второго порядка. Эллипс, гипербола. ЗадачиСкачать