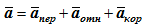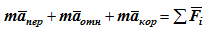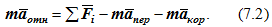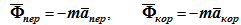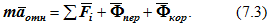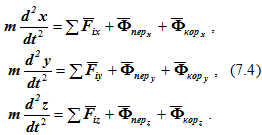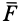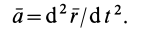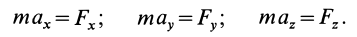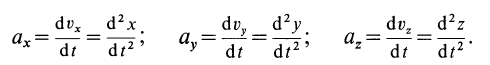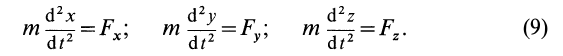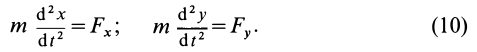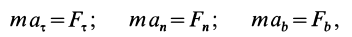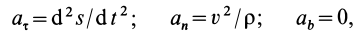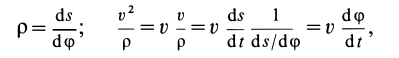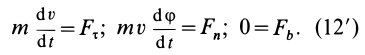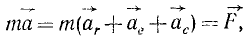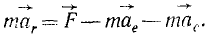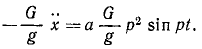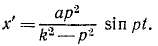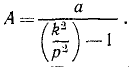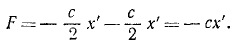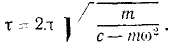- Дифференциальные уравнения относительного движения материальной точки
- iSopromat.ru
- Дифференциальные уравнения движения материальной точки в теоретической механике
- Частные случаи дифференциального уравнения движения материальной точки
- Дифференциальные уравнения относительного движения точки
- Пример решения задачи №1
- Пример решения задачи №2
- Пример решения задачи №3
- 🎬 Видео
Видео:Дифференциальные уравнения движения точкиСкачать

Дифференциальные уравнения относительного движения материальной точки
В предыдущих главах исходили из основного закона классической механики (второго закона Ньютона), который справедлив для движения по отношению к инерциальным системам отсчета. Напомним, что инерциальной («неподвижной») является такая система отсчета, по отношению к которой выполняется закон инерции. Во многих случаях необходимо исследовать движение точки по отношению к неинерциальной системе отсчета, например, по отношению к какому-либо движущемуся объекту (кораблю, автомобилю и т. д.).
Пусть материальная точка М под действием системы сил F]y F2, . Fn движется относительно системы отсчета Oxyz, которая, в
свою очередь, движется относительно инерциальной системы отсчета («неподвижных осей») OxxxyxZ-
Для решения задач динамики относительного движения материальной точки, т. е. движения материальной точки по отношению к неинерциальным, произвольно движущимся системам отсчета, необходимо найти зависимость между относительным ускорением точки аг и действующими на нее силами.
Для абсолютного движения (по отношению к «неподвижной» системе отсчета OxxxyxZ) основной закон динамики имеет вид
Из кинематики известно, что абсолютное ускорение точки равно геометрической сумме трех ускорений: относительного аг, переносного ае и кориолисова ак, т. е. а -аг +ае + ак. Подставив это значение а в равенство (15.1) и оставив в левой части уравнения таг, получим
Векторные величины Фе и Фк (численно равные произведениям тае и так и направленные противоположно ускорениям ае и ак) называют соответственно переносной и кориолисовой силами инерции.
Тогда уравнение (15.2) примет вид
Уравнение (15.4) представляет собой основное уравнение динамики для относительного движения материальной точки. Сравнивая равенства (15.1) и (15.4), заключаем, что уравнения движения материальной точки в неинерциальной системе координат составляются аналогично уравнениям абсолютного движения, но при этом к действующим на точку силам добавляются переносная и кориолисова силы инерции. Добавление сил Фе и Фк (не являющихся физическими силами, т. е. воздействиями на точку других тел) отражает кинематику движения подвижной системы отсчета Oxyz по отношению к инерциальной («неподвижной») системе отсчета OxxxyxZ-
Действительно, равенство (15.2) можно представить в виде:
В правой части этого равенства первое слагаемое выражает ускорение, которое точке сообщают действующие силы Fk, а два других слагаемых являются ускорениями, которые точка имеет вследствие движения подвижной системы отсчета. Все ускорения правой части этого равенства определяются относительно инерциальной («неподвижной») системы отсчета, а результат, т. е. аг, будет определен по отношению к подвижной системе отсчета.
Заметим, что действующие на точку силы Fk сообщают ей ускорение, равное Z Fk/m, в любой системе координат; но по отношению к инерциальной системе отсчета это будет всей величиной ускорения точки, а по отношению к неинерциальной системе отсчета — только его частью.
Рассмотрим некоторые частные случаи.
1. Пусть подвижные оси по отношению к «неподвижным» осям движутся поступательно. В этом случае угловая скорость вращения подвижных осей Oxyz будет со = 0, отсюда Фк = -2т(й>х Vr ) = 0, и закон относительного движения (15.4) принимает вид:
Отметим также, что при поступательном движении подвижной системы отсчета переносные силы инерции для всех материальных точек переносного пространства будут одинаковы, т. е. не будут зависеть от положения, занимаемого точкой в подвижной системе отсчета.
2. Пусть подвижные оси перемещаются по отношению к «неподвижным» поступательно, равномерно и прямолинейно. При таком движении осей Oxyz имеем кинематические характеристики: со = 0, а х =0, а» =0. Так как со = 0, то Фк =0, а из второго и третьего равенств получим, что ае = 0 и, следовательно, Фе =0. Тогда равенство (15.4) принимает вид
Сопоставляя равенства (15.5) и (15.1), видим, что в рассматриваемом случае дифференциальное уравнение относительного движения материальной точки совпадает с дифференциальным уравнением ее движения по отношению к неподвижным осям. Из полученного результата следует, что никаким механическим экспериментом нельзя обнаружить, находится ли данная система отсчета в покое или совершает поступательное, равномерное и прямолинейное движение по отношению к «неподвижной» системе отсчета. В этом и состоит открытый Галилеем (1638) принцип относительности классической механики.
По отношению к такой движущейся системе отсчета, как и по отношению к неподвижной, при условии Y,Fk =0 будет выполняться закон инерции. Поэтому все системы отсчета, движущиеся поступательно, равномерно и прямолинейно, а также покоящиеся, называются инерциальными. Заметим, что совпадение дифференциальных уравнений движений по отношению к «неподвижным» и подвижным осям не означает одинаковости самих движений. Ведь законы движения точки в каждой системе отсчета будут получены путем интегрирования дифференциальных уравнений. Постоянные интегрирования в уравнениях движения по отношению к разным системам отсчета будут различны, так как начальные скорости точки (являющиеся начальными условиями) по отношению к каждой системе отсчета (у которых имеется взаимное движение) будут различными.
3. Состояние относительного покоя. В этом случае по отношению к подвижным осям точка имеет такие кинематические характеристики: аг = 0 и Vr =0 и, следовательно, Фк = -2m(coxVr) =0. Тогда равенство (15.4) принимает вид
Это уравнение является уравнением относительного равновесия (покоя) точки. Заметим, что при относительном покое к точке должны быть приложены такие внешние силы, которые бы «компенсировали» переносное движение, т. е. чтобы разность ускорений Y,Fk/m-ae была равна нулю.
Задача 15.1. Определить период малых колебаний в вертикальной плоскости математического маятника (масса материальной точки т, невесомая нерастяжимая нить маятника длиной /), точка О подвеса которого движется вверх по вертикали с ускорением w (рис. 15.1).
Решение. Рассмотрим движение материальной точки как сложное, считая движение ползуна О и связанной с ним системы отсчета Оху (движется поступательно вверх с ускорением w) переносным, а движение маятника по дуге окружности радиусом ОМ= I — относительным движением по отношению к подвижной системе отсчета Оху. Длину дуги ОхМ обозначим через 5.
Так как переносное движение является поступательным (следовательно, , то после подстановки выражений для величин уравнение (б) примет вид:
Ограничимся рассмотрением малых колебаний маятника, считая угол
Ф малым и полагая приближенно sin ф — ф. Тогда, обозначив к = (g+ w)/l, предыдущее уравнение примет вид
Это дифференциальное уравнение совпадает по виду с дифференциальным уравнением (14.2) свободных прямолинейных колебаний точки, и, пользуясь результатами, полученными при его решении, определим период качания маятника:
Задача 15.2. Горизонтальная трубка ЛВ вращается вокруг вертикальной оси Z (рис. 15.2, а) с постоянной угловой скоростью со = 2 с» 1 . Внутри трубки находится шарик М массой т — 1 кг, который к точке А прикреплен пружиной; коэффициент жесткости пружины с — 8 Н/м, длина пружины в ненапряженном состоянии / = 0,5 м. В начальный момент времени /0 = 0 шарик находился в точке М0 на расстоянии АМ0 — s0 = 1,2 м и имел скорость относительно трубки VQ — 1,6 м/с, направленную от оси вращения. Определить закон движения шарика по трубке; в момент времени tx — л/2 с найти силу давления шарика на стенку трубки и силу упругости пружины.
Решение. 1. Рассмотрим движение шарика М как сложное, считая его движение вдоль трубки относительным, а вращение трубки и связанной с ней подвижной системы отсчета Oxyz — переносным движением. Начало координат О подвижной системы отсчета совместим с трубкой в точке расположения незакрепленного конца недеформированной пружины (т. е. АО — /), а ось у направим вдоль трубки от оси вращения.
Рассмотрим шарик в произвольном положении М, при котором пружина растянута, а направления векторов Vr и аг совпадают с направлением оси у (рис. 15.2, б). Hji шарик действуют сила тяжести Р, сила_упруго- сти F и реакция трубки N, которую представим составляющими Nx и Nz.
Для составления уравнения относительного движения шарика присоединим к этим силам переносную силу инерции Фе =-тае и кориолисову силу
инерции Фк—так; так как вращение трубки равномерное (со = const), то ае=а» и сила Фе направлена от оси вращения (эту силу называют еще центробежной силой инерции).
Уравнение относительного движения в векторной форме будет иметь вид
Чтобы получить дифференциальное уравнение движения точки М по трубке, спроецируем равенство (а) на ось Оу:
В нашем случае Фе — та п е — т& 2 (1 + у); F—cy. Подставив эти выражения в уравнение (б), представим его в виде
Решение неоднородного дифференциального уравнения (в) ищем как сумму общего решения (14.3) соответствующего однородного уравнения и частного решения неоднородного уравнения, т. е. у — у + _у2> где yj = = С, cos kt + С2 sin kt и у2 = D/k 2 .
Найдем еще закон изменения скорости Vr = у:
По начальным условиям при t0 = 0 у0 = 1,6 м/с, yQ = s0 — I = 0,7 м, которым должны удовлетворять функции (г) и (д), найдем С <= 0,2 м, С2 = = 0,8 м. Вычислим D/k 2 — 0,5 м. В результате общее решение (г) примет окончательный вид, м:
Это уравнение и определяет искомый закон относительного движения шарика по трубке, из которого видно, что это будет колебательное движение с круговой частотой к — 2 с -1 .
2. Рассмотрим воздействия на движущийся шарик в момент времени — л/2 с.
Сила упругости пружины F будет F, = су<, где ух = 0,2 cos л + 0,8 sin л + + 0,5 = 0,3 м. Тогда находим F, = 8 ? 0,3 = 2,4 Н.
Определим реакцию трубки. Для этого спроецируем векторное равенство (а) на оси Ох и Oz:
Кориолисова сила инерции Фк = таК — т2ыу. Из равенства (д), подставив значения С, = 0,2, С2 = 0,8 и tx = л/2 с, определим ух = —1,6 м/с. Тогда при tx — л/2 с получим Фк = 1 • 2 • 2 • (—1,6) =^6,4 Н. Знаки величин ух и Фк указывают, что реальные векторы ^ и Фк в момент времени = л/2 с будут противоположны показанным на рис. 15.2.
Подставив в равенства (е), (ж) значения Фк и P=mg, находим Nxj = —6,4 кН, Nz| = 9,81 Н. Реакция трубки при tx = л/2 с будет
Давление шарика на трубку в момент^времени tx будет численно равно Nx и направлено противоположно силе Nx.
Видео:Динамика относительного движения точки.Скачать

iSopromat.ru
Составление систем дифференциальных уравнений относительного движения точки массой m под действием сил.
Уравнение второго основного закона динамики для абсолютного движения точки массой m имеет вид
где a – абсолютное ускорение точки;
Fi – силы, действующие на точку, включая реакции связей.
Абсолютное ускорение точки в сложном движении определяется как геометрическая сумма трех ускорений: переносного aпер , относительного aотн и кориолисова aкор, т.е.
Подставляя это выражение в (7.1), получим
Введем в рассмотрение два вектора
и назовем их переносной и кориолисовой силами инерции.
Подставим эти векторы в уравнение (7.2):
Уравнение (7.3) представляет собой основное уравнение динамики относительного движения материальной точки.
В случае равномерного и поступательного переносного движения Фпер= 0, Фкор= 0 и уравнение (7.3) ничем не отличается от уравнения (7.1). Во всех инерциальных системах отсчета уравнение движения точки записывается одинаково. В этом заключается принцип относительности классической механики.
Проецируя уравнение (7.3) на оси подвижной декартовой системы координат, получим дифференциальные уравнения относительного движения точки
Дифференциальные уравнения относительного движения отличаются от дифференциальных уравнений абсолютного движения наличием в правой части уравнений проекций на соответствующие оси переносной и кориолисовой сил инерции.
Рассмотрим частные случаи относительного движения материальной точки:
- если подвижная система отсчета движется поступательно, то Фкор= 0, так как ωпер= 0, и уравнение относительного движения примет вид
Уравнение (7.6) представляет собой уравнение относительного покоя точки.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Динамика материальной точки в НИСО. Нелинейное дифференциальное уравнение движенияСкачать

Дифференциальные уравнения движения материальной точки в теоретической механике
Содержание:
Дифференциальные уравнения движения материальной точки:
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
Из кинематики точки известно, что ускорение 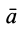
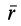
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
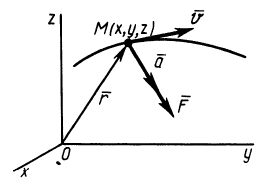
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
Видео:Дифференциальное уравнение движения материальной точки.Скачать

Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 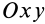
Так как 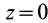
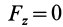
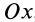
Так как при движении 
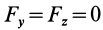
где 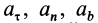
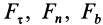
где 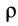
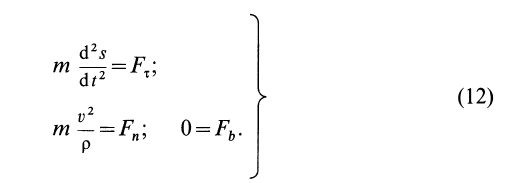
Второе уравнение из (12) можно преобразовать:
где 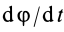
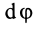
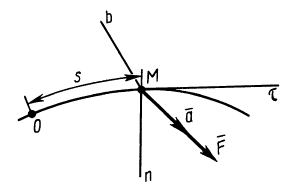
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 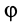
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Видео:Динамика. Введение, дифференциальные уравнения движения точки, прямая и обратная задачи динамики.Скачать

Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
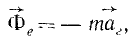
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
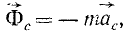
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
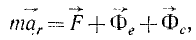
или в проекциях на оси координат:
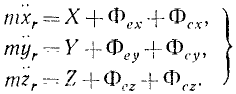
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
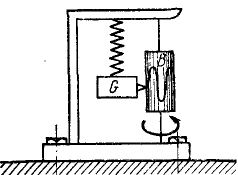
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 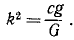
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 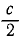
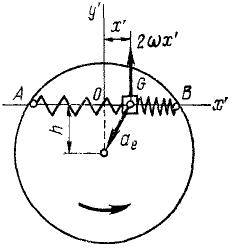
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 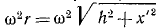
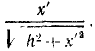
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 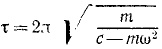
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎬 Видео
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения движения материальной точкиСкачать
Д1 Дифференциальные уравнения движения материальной точкиСкачать

Динамика относительного движенияСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Лекция 11 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ ТОЧКИ https://stepik.org/course/71088/syllabusСкачать

Дифференциальные уравнения движенияСкачать

Дифференциальные уравнения движения материальной точки. Часть 1Скачать

ДУ Уравнения, не разрешенные относительно производнойСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Теоретическая механика. Курсовая работа. Ч.1 - Исследование относительного движения.Скачать

Дифференциальные уравнения поступательного, вращательного и плоского движенияСкачать