Составить блок схему линейного уравнения

Видео:0.Блок схема. 8 классСкачать

Составить блок схему линейного уравнения

Блок 1. Линейные уравнения и неравенства с параметрами

Покажем решение линейного уравнения , где a -параметр, k ( a ), b ( a )-выражения, содержащие параметр. В общем виде решение удобнее всего изобразить следующей блок-схемой (рис.1).

SHAPE * MERGEFORMAT

бесконечно много корней, т.е.

Рис.1. Блок-схема решения линейного уравнения.

Эта блок-схема удобна тем, что идеально отражает обычное для задач с параметрами «ветвление» решения в зависимости от значений параметра. Мы видим, что из одного уравнения возникает три уравнения: , каждое из которых уже решается единым, определенным, стандартным способом.

Добавим, что в рассмотренной блок-схеме предполагается, что все значения и переменной x , и параметра a являются допустимыми. Если это не так, т.е. при определенных значениях x и a уравнение не имеет смысла, то решение усложняется. Возникает необходимость во-первых, определить эти недопустимые значения, а во-вторых, учесть их в процессе решения.

Часто в задачах на линейные уравнения и неравенства с параметрами бывает полезно «опереться» на линейную функцию , где k , b -коэффициенты. Напомним график линейной функции (рис.2).

SHAPE * MERGEFORMAT

Рис.2. График линейной функции.

Это, как известно, прямая, расположенная под углом к положительному направлению оси OX и отсекающая на оси ординат отрезок b . Важно помнить, что и коэффициент k называется угловым коэффициентом. Очевидно, в задачах с параметрами на линейную функцию ее записывают в таком виде: , где a -параметр. В зависимости от a графиками здесь является множество всевозможных прямых на координатной плоскости ( XOY ). Полезно помнить, что линейная функция не «описывает» прямые, которые параллельны оси ординат ( ).

В этом же модуле рассмотрим тему «Системы двух линейных уравнений с двумя неизвестными с параметрами».

Решить такую систему – значит найти такие пары чисел , которые являются решениями и первого и второго уравнений одновременно. Собственно решения можно находить двумя популярными в школьном курсе приемами: подстановкой или «сложением-вычитанием» уравнений. Однако в задачах с параметрами требуется еще и исследовать количество решений в зависимости от параметра a . Чтобы наглядней понять смысл дальнейшего алгоритма решений подобных задач, запишем каждое уравнение системы через линейную функцию.

Учитывая тот факт, что каждое уравнение системы геометрически представляет прямую на плоскости, возможны три случая расположения двух прямых, а, следовательно, три случая решения системы.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Основные блок-схемы решения линейных и квадратичных задач с параметрами

Разделы: Математика

Задачи с параметрами (ЗсП) традиционно являются наиболее сложными для учащихся, поскольку требуют от них умения логически рассуждать и проводить анализ решения. Подобные задачи являются первыми исследовательскими задачами, с которыми встречаются школьники. Для их решения не требуются знания, выходящие за пределы школьной программы, но недостаточно применения лишь стандартных приемов, а необходимо глубокое понимание всех разделов элементарной математики.

В данной статье предпринята попытка систематизации и формализации (в форме блок-схем) наиболее часто встречающихся и наиболее типичных ЗсП. При этом выделены классы задач, решаемых по единой методике.

Рассматриваются аналитические методы решения ЗсП, сводящиеся к исследованию линейных или квадратных уравнений (неравенств), а также квадратного трехчлена. Такой выбор обусловлен тем, что курс школьной математики ограничен «вглубь», по существу, «теорией квадратичного».

Линейные уравнения

Определение. Уравнение вида ax=b, где a, b принадлежат множеству всех действительных чисел, будем называть стандартным видом линейного уравнения. Всевозможные варианты, возникающие при решении линейных уравнений, отразим в блок–схеме I.

Количество корней линейного уравнения отразим в блок-схеме II:

Пример 1. Для всех действительных значений параметра m решите уравнение m 2 x–2=4x+m.

Решение. Приведем заданное линейное уравнение к стандартному виду:

m 2 x–2=4x+m, m 2 x–4x=m+2, (m 2 –4)x=m+2.(1)

Следуя схеме I, рассмотрим два случая для коэффициента при x:

1)если m 2 – 4 не равно 0, m не равно ±2, то x=(m+2)/(m 2 -4), x=1/(m–2);

а) при m = –2 уравнение (1) примет вид 0х=0, отсюда х – любое действительное число;

б) при m = 2 уравнение (1) примет вид 0х= 4, отсюда следует, что корней нет.

Ответ. Если m 2 то x=1/(m–2); если m= – 2, то x – любое действительное число; если m=2, то корней нет.

Пример 2. При каких значениях параметра k уравнение 2(k–2x)=kx+3 не имеет корней?

Решение. 2(k–2x)=kx+3, (k+4)x=2k–3. В силу схемы II уравнение не имеет корней, если k+4=0 и 2k–3 не равно 0 => k= –4 и k не равно 1,5 => k = –4.

Ответ. k=–4.

Системы линейных уравнений

Определение 1. Система называется совместной, если она имеет хотя бы одно решение.

Определение 2. Система называется несовместной, если она не имеет ни одного решения.

Количество решений системы линейных уравнений отразим в блок-схеме III.

Замечание. Так как уравнение прямой y=kx+b в общем виде записывается следующим образом ax+by+c=0, то взаимное расположение двух прямых отразим в блок-схеме IV.

Пример. При каких значениях параметра c система из двух уравнений c 2 x+(2–c)y–4=c3 и (2c–1)y+cx+2=c 5 совместна?

Решение. Запишем систему в стандартном виде: c 2 x+(2–c)y=c 3 +4 и cx+(2c–1)y=c 5 –2. Сначала найдем значения c, при которых эта система не имеет решений. В силу схемы III имеем условие,

c 2 /с=(2-с)/(2с–1), с не равно (c 3 +4)/(c 5 –2),

которое равносильно системе из уравнения и неравенства

с=(2–с)/(2с–1) и с не равно (c 3 +4)/(c 5 –2).

Решением системы является с=1. Итак, система имеет решения при всех действительных значениях с, кроме с=1.

Ответ. с — любое действительное число, с не равно 1.

Линейные неравенства

Определение. Неравенство вида ax>b, ax b, ax b, отразим в блок-схеме V.

Пример. Для всех значений параметра m решите неравенство 5x–m>mx–3.

Решение. 5x–m>mx–3, (5–m)x>m–3.

Следуя схеме V, рассмотрим три случая для коэффициента при х:

2)если 5–m 5, то x 2. Откуда следует, что решений нет.

Ответ. Если m (m–3)/(5–m); если m=5, то решений нет; если m>5, то х 2 +bx+c=0, где a, b, c — любые действительные числа, a>0, называется квадратным уравнением относительно действительного переменного x.

Ситуации, возникающие при решении квадратных уравнений, отразим в блок–схеме VI.

Пример. При каких значениях параметра c уравнение (c–2)x 2 +2(с–2)x+2=0 не имеет корней?

Решение. Рассмотрим два случая:

1) если с–2 не равно 0, c не равно 2, то D 2 –2(c–2) 2 +(c+4)x+c+7=0 имеет только отрицательные корни?

Решение. В силу условия задачи необходимо рассмотреть два случая (линейный и квадратичный):

1) если c–1=0, c=1, то уравнение примет вид 5x+8=0, x= –5/8 – отрицательный корень;

2) если c–1 не равно 0, c не равно 1, то, следуя схеме VII, получим систему

Решением ее являются промежутки –22/3 2 +bx+c, где a не равно 0, называется квадратичной. График квадратичной функции называется параболой.

Абсциссы точек пересечения параболы y=ax 2 +bx+c с осью (Ox) являются корнями уравнения ax 2 +bx+c=0.

Учитывая это, отразим взаимное расположение параболы и оси (Ox) в следующей схеме:

Замечание. Если уравнение параболы имеет вид y=a(x–p) 2 +q, то (p; q) – координаты вершины параболы.

Пример 1. При каких значениях параметра a вершина параболы y=(x–7a) 2 +a 2 –10+3a лежит в III координатной четверти?

Решение. Пусть (x₀, y₀) – координаты вершины параболы. В силу замечания имеем x₀=7a, y₀=a 2 –10+3a. Так как вершина параболы лежит в третьей четверти, то

Ответ. –5

Пример 2. При каких значениях параметра b график функции y=(4–b 2 )x 2 +2(b+2)x–1 лежит ниже оси (Ox)?

Решение. Рассмотрим два случая.

1. Пусть 4–b 2 =0, b= + 2;

1) если b=2, то прямая y=8x–1 не лежит ниже оси (Ox);

2) если b= –2, то прямая y= –1 лежит ниже оси (Ox).

2. Пусть 4–b 2 не равно 0. Тогда в соответствии со схемой VIII получим

Объединяя ответы, получим b 2 +bx+c=0. Введем функцию y(x)= ax 2 +bx+c. Тогда расположение корней этого уравнения на числовой оси отразим в блок–схеме IX.

Следствие. С учетом схемы IX схема VII для знаков корней квадратного уравнения примет следующий вид:

Пример. При каких значениях параметра a корни уравнения x 2 –2(a+3)x+a 2 +6,25a+8=0 больше 2?

Решение. Введем функцию y(x)=x 2 –2(a+3)x+a 2 +6,25a+8; x₀ – абсцисса вершины этой параболы. Так как корни уравнения находятся справа от числа 2, то в соответствии со схемой IX имеем:

Решение. Данная задача равносильна следующей: при каких значениях параметра b система

имеет одно решение?

Решим неравенство (2): 2x 2 –2x–1>0, x_1,2=0,5(1±(3) 1/2 ), x 1/2 ) или x>0,5(1+(3) 1/2 ).

Найдем корни уравнения (1): D=(2b–7) 2 , x₁=2, x₂=2b–5. Поскольку корень x₁=2 удовлетворяет неравенству (2), то система имеет одно решение в следующих случаях:

1) если x₂=2b–5 не удовлетворяет неравенству (2), то 0,5(1–(3) 1/2 ) 1/2 ) или 0,25(11–O3) 1/2 );

Ответ. 0,25(11–(3) 1/2 ) 1/2 ), b=3,5.

Пример 2. При каких значениях параметра p уравнение 5–4sin 2 x–8cos 2 (x/2)=3p имеет корни?

Решение. Преобразуем заданное уравнение:

5– 4sin 2 x–8cos 2 (x/2)=3p => 5–4(1–cos2x)–4(1+cosx)=3p => 4cos 2 x–4cosx–3p–3=0.

Сделаем замену cosx=t. Тогда заданная задача равносильна следующей: при каких значениях p система

4t2–4t–3p–3=0, (1)
-1 2 –4t–3p–3; t₀–вершина этой параболы. В силу схемы IX случаи 1, 2 и 3 описываются следующей совокупностью:

Видео:Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать

Линейный алгоритм. Понятие и особенности. Блок-схема

Каждый человек на протяжении своей жизни решает множество задач разной сложности. Но даже самые простые из задач выполняются последовательно, то есть за несколько шагов. Эту последовательность можно назвать алгоритмом. Последовательности бывают разные, но начинать их изучение лучше всего с линейных.

Прежде чем приступить к рассмотрению основной темы статьи, следует сделать краткое отступление и сказать несколько слов про алгоритмический язык.

Видео:Самый подробный урок про Блок-схемы, Понимание, Чтение и Создание блок-схемСкачать

Алгоритмический язык

Представьте, что человеку, работающему за компьютером, поставлена некая вычислительная задача. В языке программирования решение этой задачи выполняется с помощью алгоритмизации. Решение предполагает: — разбиение на этапы; — разработку алгоритма; — составление программы решения на алгоритмическом языке; — ввод данных; — отладку программы (возможны ошибки — их надо исправить); — выполнение на ПК; — анализ результатов.

Алгоритмический язык является средством описания алгоритмов, а уже алгоритм, в свою очередь, представляет собой чёткое описание определённой последовательности действий, направленных на решение необходимой задачи.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Свойства алгоритма

Их несколько: — конечность. Любой алгоритм должен быть завершённым, а окончание наступает после выполнения определённого числа шагов; — однозначность, понятность. Не допускается разных толкований, неопределённости и двусмысленности — всё должно быть чётко и ясно, а также понятно исполнителю — и правила выполнения действий линейного алгоритма, и сами действия; — результативность. Итог работы — результат, полученный за конечное число шагов; — универсальность, массовость. Качественный алгоритм способен решать не одну задачу, а целый класс задач, имеющих схожую постановку/структуру.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Линейная структура

Любой алгоритм составляется из ряда базовых структур. Простейшей базовой структурой является следование — структура с линейными характеристиками. Из этого можно сформулировать определение.

Линейный алгоритм — это алгоритм, образуемый командами, которые выполняются однократно и именно в той последовательности, в которой записаны. Линейная структура, по сути, проста. Записать её можно как в текстовой, так и в графической форме.

Представим, что у нас стоит задача пропылесосить ковёр в комнате. В текстовой форме алгоритм будет следующим: — принести пылесос к месту уборки; — включить; — пропылесосить; — выключить; — унести пылесос.

И каждый раз, когда нам надо будет пылесосить, мы будем выполнять один и тот же алгоритм.

Теперь поговорим про графическую форму представления.

Блок-схема

Для изображения алгоритма графически используют блок-схемы. Они представляют собой геометрические фигуры (блоки), соединённые стрелками. Стрелки показывают связь между этапами и последовательность их выполнения. Каждый блок сопровождается надписью.

Рассмотрим фигуры, которые используются при визуализации типичной линейной последовательности.

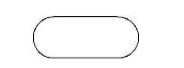
Блок ввода-вывода данных (отображает список вводимых и выводимых переменных):

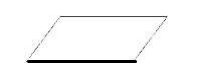
Арифметический блок (отображает арифметическую операцию/группу операций):

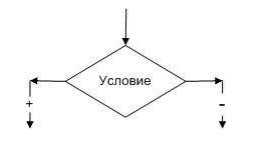
Условный блок (позволяет описать условие). Алгоритмы с таким блоком используются при графической визуализации алгоритмов с ветвлением:

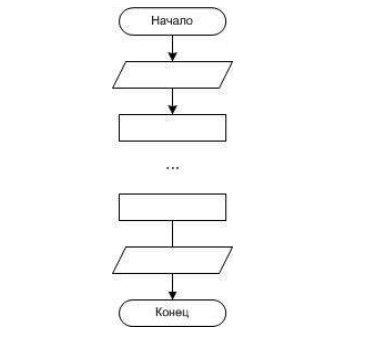
Условного блока нет в классическом линейном алгоритме, так как в нём, как уже было сказано ранее, все операции выполняются последовательно, то есть одна за другой. В линейном алгоритме размещение блоков выглядит следующим образом:

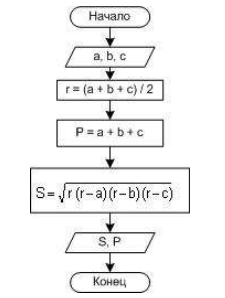
А вот, как решается задача по нахождению площади треугольника по формуле Герона. Здесь a, b, c – это длины сторон, S – площадь треугольника, P – периметр.

Следует обратить внимание, что запись «=» — это не математическое равенство, а операция присваивания. В результате этой операции переменная, стоящая слева от оператора, получает значение, которое указано справа. Значение не обязательно должно быть сразу определено (a = 3) — оно может вычисляться посредством выражения (a = b + z), где b = 1, a z = 2.

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Примеры линейных алгоритмов

Если рассмотреть примеры решения на языке Pascal (именно этот язык до сих пор используется для изучения основ алгоритмизации и программирования), то можно увидеть следующую картину:

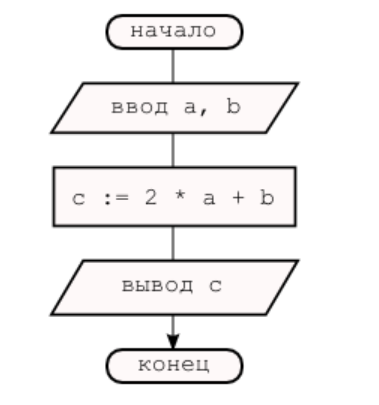
И, соответственно, блок-схема программы линейной структуры будет выглядеть следующим образом:

Видео:Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Как составить программу линейной структуры?

Порядок следующий: — определите, что именно относится к исходным данными, а также каков типы/класс этих данных, выберите имена переменных; — определите, каков тип данных будет у искомого результата, выберите название переменных (переменной); — определите, какие математические формулы связывают результат и исходные данные; — если требуется наличие промежуточных данных, определите класс/типы этих данных и выберите имена; — опишите все используемые переменные; — запишите окончательный алгоритм. Он должен включать в себя ввод данных, вычисления, вывод результатов.

На этом всё, в следующий раз рассмотрим на примерах программу разветвлённой структуры. Если же вас интересует тема алгоритмизации в контексте разработки программного обеспечения, ждём вас на профессиональном курсе OTUS!

📺 Видео

Линейное уравнение с одной переменной. 6 класс.Скачать

3 Линейный алгоритм в блок-схеме: 2 примера за 2 мин, как сделать блок-схему для линейного алгоритмаСкачать

Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Решаем линейные уравнения на ОГЭ по математике 2022. Блок №1Скачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

7 класс, 5 урок, Задачи на составление линейных уравнений с одной переменнойСкачать

7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Линейные блок-схемыСкачать

Блок схема алгоритма (часть 1)Скачать