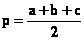Составить блок схему для решения квадратного уравнения ax2 bx c

6.2. ОСНОВНЫЕ ТИПЫ ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМОВ

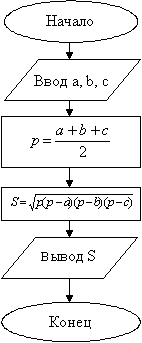
Наиболее простым видом алгоритма является линейный алгоритм, при котором действия выполняются последовательно, одно за другим, без разветвлений и возвратов.

Пример . Вычисление площади треугольника по трем сторонам a , b , c по формуле Герона:

, где

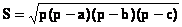
Блок-схема алгоритма имеет вид:

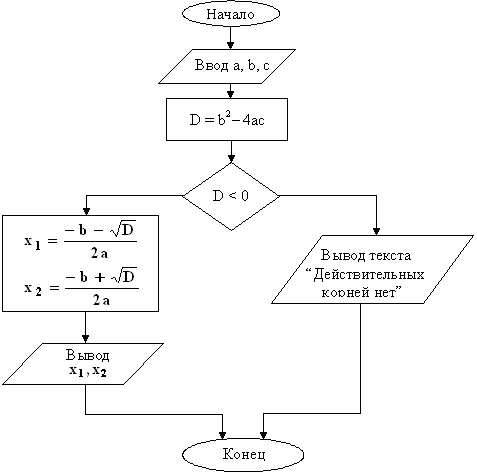
В процессе решения многих задач часто возникает необходимость в зависимости от исходных данных или получающихся промежуточных результатов проводить вычисления либо по одним, либо по другим формулам, т.е. по разным направлениям – ветвям. Такой вычислительный алгоритм называется разветвляющимся.

Пример. Нахождение действительных корней квадратного уравнения

Блок-схема алгоритма имеет вид:

При решении большинства практических задач возникает необходимость неоднократного повторения однотипных действий при различных значениях параметров, определяющих эти действия. Такие алгоритмы называются циклическими, а повторяемые участки вычислений – циклами.

Пример . Вычисление факториала натурального числа

Видео:Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать

Один из методов решения квадратных уравнений

Алгоритм решения данной задачи сначала должен быть представлен в виде словесного описания или графически в виде блок-схемы. Алгоритм вычисления корней квадратного уравнения может быть представлен в виде блок-схем, изображенных на рисунках, отображающих основные элементы блок-схем и алгоритм вычисления корней квадратного уравнения:

Изображение алгоритма в виде блок-схемы позволяет наглядно представить последовательность действий, необходимых для решения поставленной задачи, убедиться самому программисту в правильности понимания поставленной задачи.

После разработки алгоритма решения задачи и представления его в виде блок-схемы можно перейти к написанию программы – последовательности инструкций на выбранном языке программирования, соответствующей разработанному алгоритму. Например, ниже приведен фрагмент программы решения квадратного уравнения, соответствующий приведенному выше алгоритму, составленному на языке Visual Basic.

procedure SqRoot(Editi,Edit2,Edit3:tEdit;Label2:tLabel);
var
a,b,c:real;
d:real;
xl,x2:real;
begin
a:=StrToFloat(Editl.text);
b:=StrToFloat(Edit2.text);
с:=StrToFloat(Edj.t3.text);
d:=Sqr(b)-4*a*c;
if d=0 then begin
Label2.color:=clRed;
Label2.font.color:=clRed;
Label2.caption:=’Дискриминант меньше нуля.’+#13+
‘Уравнение не имеет корней.’ end else
begin

х1:=(-b+Sqrt(d))/(2*a);
x2:=(-b-Sqrt(d))/(2*а);

Label2.font.color:=clBlack;
Label 2.caption=’Корни уравнения:’ +#13+’xl=1+FloatToStr(xl)
+#13+’x2=’+FloatToStr(x2);
end;
end.

Но программа, написанная на языке программирования, состоит из инструкций, понятных человеку, но не понятных процессору компьютера. Поэтому чтобы процессор смог выполнить работу в соответствии с инструкциями исходной программы, она должна быть переведена на язык команд процессора, то есть машинный язык. Задачу преобразования исходной программы в машинный код выполняет специальная программа — компилятор. Помимо преобразования исходной программы в машинную, компилятор выполняет проверку правильности записи инструкций исходной программы, т. е. осуществляет синтаксический анализ.

Компилятор создает исполняемую программу только в том случае, если в тексте исходной программы нет синтаксических ошибок. Однако генерация исполняемой программы машинного кода свидетельствует только об отсутствии в тексте программы синтаксических ошибок. Убедиться в правильности работы программы можно только во время ее тестирования – пробных запусках программы и при анализе полученных результатов. Например, если в программе нахождения корней квадратного уравнения допущена ошибка в записи выражения вычисления дискриминанта, то даже если это выражение будет синтаксически верно, программа выдаст неверные значения корней.

Решение квадратных уравнений средствами Visual Basic

Задача: Дано квадратное уравнение общего вида: ax 2 +bx+c=0. Ввести в память компьютера числовые коэффициенты: a, b, c, выполнить необходимый анализ введенной информации согласно известному из курса средней школы алгоритму решения квадратного уравнения: найти дискриминант d=b 2 -4ac и, проанализировав его знак, найти все действительные корни, если знак дискриминанта положительный, или сообщить о том, что действительных корней нет, если знак дискриминанта отрицательный.

Начать составление проекта решения данной задачи необходимо с ответа на вопрос: что нужно поместить на форму Form1?

Поместим на форму две кнопки: CommandButton1 и CommandButton2.

Для этого нужно воспользоваться Панелью элементов (объектов) управления General, которая расположена в левой части основного окна компилятора Visual Basic.

Первая кнопка CommandButton1 предназначается для начала работы программы согласно следующему алгоритму:

1. ввод коэффициентов исходного уравнения a, b, c;
2. расчет дискриминанта d=b 2 — 4ac;
3. анализ знака дискриминанта, вычисление корней уравнения и вывод их на форму, если знак дискриминанта d>0 (положительный);
4. вывод сообщения: «Решений нет», если знак дискриминанта d 2 -5x+6=0.

Далее рассмотрим процесс решения второго квадратного уравнения: 10x 2 +5x+200=0.

В окне InputBox вводим значение первого коэффициента уравнения a=10.

Ввод первого коэффициента a завершается нажатием кнопки Ok.

Аналогично в окне InputBox вводим значение второго коэффициента уравнения b=5.

Ввод второго коэффициента b так же завершается нажатием соответствующей кнопки Ok.

Наконец, в окне InputBox вводим значение третьего коэффициента нового уравнения c=200.

Ввод третьего коэффициента c так же завершается нажатием соответствующей кнопки Ok.

После этого программа, проанализировав полученную информацию, должна выдать в окне формы соответствующее сообщение о том, что данное уравнение не имеет решений.

И, наконец, рассмотрим процесс решения третьего квадратного уравнения: x 2 -8x+16=0.

Это уравнение имеет двукратный корень, так как его дискриминант d=0. Как и в двух предыдущих случаях, вводим коэффициенты квадратного уравнения. Первым вводим коэффициент a=1.

Далее вводим второй коэффициент уравнения b= –8.

Третий коэффициент уравнения c=16 вводим в последнюю очередь.

В итоге мы должны увидеть правильное решение третьего квадратного уравнения. Действительно последнее уравнение имеет два одинаковых корня.

Видео:0.Блок схема. 8 классСкачать

Блок — схема к теме «Виды квадратных уравнений и методы их решения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Видеолекции для
профессионалов

• Свидетельства для портфолио
• Вечный доступ за 120 рублей
• 311 видеолекции для каждого

Решение квадратного уравнения.

Квадратным называется уравнение вида ax 2 + bx + c = 0, где a , b , c – числа, a ≠ 0.

(Если требуется, то привести уравнение к указанному виду, выполнив необходимые преобразования (перенести слагаемые, раскрыть скобки, применить формулы сокращенного умножения))

неполное квадратное уравнение

полное квадратное уравнение

(если возможно, то сократить коэффициенты a , b , c на общий множитель)

с = 0 разложение на множители

x = 0 или ax + b = 0

x =

х =0 или 5х – 2 = 0

b = 0 привести к уравнению вида ax 2 = t

если t / a > 0, то

x = +

если t / a

4х 2 – 9 = 0 6х 2 + 24 = 0

4х 2 = 9 6х 2 = -24

х = + 1,5 корней нет

Ответ: +1,5 Ответ: к.н.

х 2 + bx + c = 0 – приведенное квадратное уравнение

х₁ + х₂ = -1, х_{1 =} — 8,

ax 2 +bx + c = 0

D > 0 2 корня

D = 0 1 корень

D

х₁ =

х₂ =

1. 2х 2 – 9х + 10 = 0

D = 81 – 80 = 1 > 0 2к.

2. 3х 2 +5х + 6 = 0

Ответ: корней нет.

ax 2 +bx + c = 0

b = 2к

D ₁ > 0 2 корня

D ₁ = 0 1 корень

D ₁

2. х₁ =

х₂ =

5х 2 + 14х — 3 = 0

D₁ = 49 + 15 = 64 > 0 2к.

a + b + c = 0

1. 3х 2 – 12 = 0
2. 9у 2 – 4 = 0
3. х 2 -3х = 0
4. 6у – у 2 = 0
5. 0,2х 2 – 1,8х = 0
6. (у — 1) 2 — 1 = 0
7. 5х = 3х 2
8. 7х 2 – 4 = 5
9. х 2 – 5х + 6 = 0
10. у 2 + 8у + 15 = 0
11. z 2 – 3z – 10 = 0
12. 3x 2 – 5x + 2= 0
13. 2x – x 2 + 3 = 0
14. (3 – 2x)(6x – 1) = (2x – 3) 2
15. (5 +4x) 2 = (9 – 21x)(4x +5)

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Ментальная арифметика: умножение и деление

• Сейчас обучается 80 человек из 37 регионов

Курс повышения квалификации

Профессиональные компетенции педагога в рамках Федерального закона «Об образовании в Российской Федерации» №273-ФЗ от 29.12.2012

Курс повышения квалификации

Развитие предметных навыков при подготовке младших школьников к олимпиадам по математике

• Курс добавлен 28.02.2022

«Обзор традиционных и современных методик для формирования навыков арифметических вычислений в уме у младших школьников»

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Видео:Самый подробный урок про Блок-схемы, Понимание, Чтение и Создание блок-схемСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 858 504 материала в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 08.02.2017
• 473
• 2

• 08.02.2017
• 809
• 2

• 08.02.2017
• 502
• 2

• 08.02.2017
• 366
• 0

• 08.02.2017
• 332
• 0

• 08.02.2017
• 296
• 0

• 08.02.2017
• 313
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 08.02.2017 2390
• DOCX 48 кбайт
• 12 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Дормидонтова Наталья Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 6 месяцев
• Подписчики: 0
• Всего просмотров: 10493
• Всего материалов: 5

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

«Дети с УО в семье и школе»

«Профилактика эмоционального и профессионального выгорания педагога через самооценку профессиональной деятельности»

«Актуальные и современные проблемы системы образования»

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В школах России пройдет урок, посвященный Великой Отечественной войне

Время чтения: 2 минуты

Тысячи учителей в Австралии вышли на забастовку

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Алгебра 8 класс (Урок№28 - Решение квадратных уравнений вида ax2 + bx + c = 0.Формула корней кв.ур.)Скачать

Решить квадратное уравнение

Формулировка. Даны вещественные числа a, b и c, причем a отлично от 0. Решить квадратное уравнение ax 2 + bx + c = 0 или сообщить о том, что действительных решений нет.

Решение. Из алгебры известно, что:

– если D > 0, имеет два решения: , ;

– если D = 0, имеет единственное решение: ;

– если D 0 then begin

x1 := (-b + sqrt(d)) / 2 * a;

x2 := (-b — sqrt(d)) / 2 * a;

writeln(‘x1 = ‘, x1:4:2, ‘, x2 = ‘, x2:4:2)

Код:

1. program QuadraticEquation;
2. var
3. a, b, c, d, x1, x2: real;
4. begin
5. readln(a, b, c);
6. d := b * b — 4 * a * c;
7. if d >= 0 then begin
8. if d 0 then begin
9. x1 := (-b + sqrt(d)) / 2 * a;
10. x2 := (-b — sqrt(d)) / 2 * a;
11. writeln(‘x1 = ‘, x1:4:2, ‘, x2 = ‘, x2:4:2)
12. end
13. else begin
14. x1 := -(b / 2 * a);
15. writeln(‘x = ‘, x1:4:2)
16. end
17. end
18. else begin
19. writeln(‘No real solutions!’);
20. end
21. end.

🎬 Видео

Решаем задачи в виде блок-схемы (7 класс)Скачать

Быстрый способ решения квадратного уравненияСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Как решать квадратные уравнения без дискриминантаСкачать

Алгоритм решения квадратного уравненияСкачать

Геометрический способ решения квадратных уравнений. Без дискриминанта!Скачать

Метод выделения полного квадрата. 8 класс.Скачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Блок-схема циклического алгоритма. Вычисление n!Скачать

решаем квадратные уравнения в ExcelСкачать

ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Алгоритм решения квадратного уравнения | Алгебра 8 класс #35 | ИнфоурокСкачать

Блок схема алгоритма (часть 2)Скачать

Теорема Виета. 8 класс.Скачать