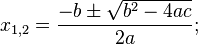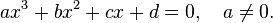Составить алгоритм и программу поиска корней кубического и трансцендентного уравнений c

Видео:Кубические уравнения. Деление столбиком. Схема Горнера.Скачать

Составить алгоритм и программу поиска корней кубического и трансцендентного уравнений c

Модуль состоит из двух файлов, poly34.h, poly34.cpp.
Для его работы не требуются никакие дополнительные библиотеки.
Из стандартных include-файлов подключается только math.h.
Динамическое выделение памяти также не используется.

poly34.h — заголовочный файл
poly34.cpp — реализация.

Уравнения степени 3

Линейные и квадратные уравнения с действительными коэффициентами решаются просто. Для решения кубических уравнений можно взять триногометрическую формулу Виета, код программы занимает около двух десятков строк. Корни уравнения x 3 + ax 2 + bx + c = 0 находятся с помощью функции Здесь x должен быть маccивом длины 3.

В случае трех действительных корней функция возвращает число 3, сами корни возвращаются в x[0],x[1],x[2].

Замечание 1. Корни не обязательно упорядочены!
Если два корня совпадают, то функция возвращает число 2, а в массиве x по-прежнему лежат три числа.

Если функция возвращает 1, то x[0] — действительный корень и x[1]±i*x[2] — пара комплексно сопряженных.

Замечание 2. Из-за погрешностей округления пара комплексно сопряженных корней с очень малой мнимой частью иногда может оказаться действительным корнем кратности 2. Например, для уравнения x 3 — 5x 2 + 8x — 4 = 0 с корнями 1,2,2 получаются корни 1.0, 2.0±i*9.6e-17. Если мнимая часть корня по модулю не превышает 1e-14, то функция SolveP3 сама заменяет такую пару на один действительный двукратный корень, но пользователь должен все равно иметь в виду возможность такой ситуации.

Уравнения степени 4

Для решения уравнений 4-й степени лучше взять решение Декарта — Эйлера. Корни уравнения x 4 + ax 3 + bx 2 + cx + d = 0 находятся с помощью функции Здесь x должен быть маccивом длины 4.

В случае 4-х действительных корней функция возвращает число 4, сами корни возвращаются в x[0],x[1],x[2],x[3].

В случае 2-х действительных и пары комплексно сопряженных корней функция возвращает число 2, x[0],x[1] — действительные корни и x[2]±i*x[3] — пара комплексно сопряженных.

Если уравнение имеет две пары пары комплексно сопряженных корней, то функция возвращает 0, x[0]±i*x[1] и x[2]±i*x[3] — сами корни.
Замечание 3. Численные эксперименты показывают, что в отдельных случаях получающаяся погрешность, довольно велика, до 10 -12 . Поэтому в конце найденные действительные корни уточняются с помощью одного шага метода Ньютона.
Например, для уравнения x*(x-1)*(x-0.0001)*(x-0.0002) без уточнения погрешность будет порядка 0.25*10 -9 , с уточнением порядка 10 -16 .

Уравнения степени 5

Все корни уравнения 5-й степени f(x) = x 5 + ax 4 + bx 3 + cx 2 + dx + e = 0 не превосходят по модулю величины brd = 1 + max( |a|, |b|, |c|, |d|, |e| ).

Уравнение 5-й степени всегда имеет по крайней мере один действительный корень. Для его нахождения, начиная с интервала [-brd,brd] сделаем 6 «делений отрезка пополам». После этого уточним корень методом Ньютона.

Найдя один действительный корень x₀, поделим на него исходный многочлен f(x) и найдем корни полученного многочлена 4-й степени.

Корни многочлена f(x) находятся с помощью функции Здесь x должен быть маccивом длины 5.

В случае 5 действительных корней функция возвращает число 5, сами корни возвращаются в x[0],x[1],x[2],x[3],x[4].

В случае 3-х действительных и пары комплексно сопряженных корней функция возвращает число 3, x[0],x[1],x[2] — действительные корни и x[3]±i*x[4] — пара комплексно сопряженных.

Если уравнение имеет две пары пары комплексно сопряженных корней, то функция возвращает 1, x[0] — действительный корень и x[1]±i*x[2] , x[3]±i*x[4] — комплексные корни.

Вспомогательные функции

Решение кубических уравнений производится в одной-единственной функции SolveP3. Для решения уравнений 4-й степени используются три вспомогательных функции:

Первая служит для извлечения квадратного корня из комплексного числа: a+i*s = sqrt(x+i*y).

Вторая — для решения биквадратного уравнения, третья — для решения неполного уравнения.
Замечание 4. Как и в случае кубических уравнений, корень кратности 2 или пара очень близких действительных корней может быть показана в виде пары комплексно сопряженных корней с малой мнимой частью.

Для решения уравнений 5-й степени используются функции:

Видео:✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Решение кубического уравнения

Written on 13 Мая 2007 .

ОГЛАВЛЕНИЕ

Кубическое уравнение записывается в виде:

x 3 +a*x 2 +b*x+c=0.

Для нахождения его корней, в случае действительных коэффициентов, вначале вычисляются: Q=(a 2 -3b)/9, R=(2a 3 -9ab+27c)/54.

Далее, если R 2 3 , то уравнение имеет три действительных корня, вычисляющихся по формулам (Виета): t=acos(R/sqrt(Q 3 ))/3,
x₁=-2*sqrt(Q)cos(t)-a/3,
x₂=-2*sqrt(Q)cos(t+(2*pi/3))-a/3,
x₃=-2*sqrt(Q)cos(t-(2*pi/3))-a/3.

В том случае, когда R 2 >=Q 3 , то действительных корней один (общий случай) или два (вырожденные случаи). Кроме действительного корня, имеется два комплексно-сопряженных. Для их нахождения вычисляются (формула Кардано):
A=-sign(R)[|R|+sqrt(R 2 -Q 3 )] 1/3 ,
B=Q/A при A!=0 или B=0 при A=0.

Действительный корень будет:
x₁=(A+B)-a/3.

Комплексно-сопряженные корни: x_2,3=-(A+B)/2-a/3 + i*sqrt(3)*(A-B)/2
В том случае, когда A=B, то комплексно-сопряженные корни вырождаются в действительный:
x₂=-A-a/3.

Формулы Кардано и Виета требуют применения специальных функций, и в том случае, когда требуется провести большую серию вычислений корней кубического уравнения с не слишком сильно меняющимися коэффициентами, более быстрым алгоритмом является использование метода Ньютона или других итерационных методов (с нахождением начального приближения по формулам Кардано-Виета).

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Поиск по сайту

Выражение вида f(x)=0 называется уравнением. Число х называется корнем уравнения, если при его подстановке уравнение обращается в верное равенство. В статье рассмотрим методы решения уравнений — как точных, так и численных (приближенных).

Видео:Математика | Кубические уравнения по методу СталлонеСкачать

Решение квадратных уравнений

Квадратным уравнением называется уравнение вида

Классическая формула для нахождения его корней (действительных и комплексных):

где выражение D = b 2 − 4ac называется дискриминантом уравнения, от его значения зависит количество и характер решений:

• Если D>0, то корней уравнения будет два и оба они будут действительными числами;
• Если D=0, то будет лишь один дейсвительный корень уравнения;
• Если D 2 +10x+200=0; данное уравнение не имеет действительных корней, но имеет пару сопряженных комплексных корней: x₁ = -1-6,2449979983984i, x₂ = -1+6,2449979983984i;
• x 2 -8x+16=0; данное уравнение имеет один двукратный корень x₁=x₂=4;
• x 2 -5x+6=0; данное уравнение имеет два различных корня x₁=2, x₂=3.

Напишем программу для решения этих уравнений:

На выходе получим:

5x^2 — 10x + 200 = 0
x0 = (-1, -6,2449979983984)
x1 = (-1, 6,2449979983984)

x^2 — 8x + 16 = 0
x0 = (4, 0)
x1 = (4, 0)

x^2 — 5x + 6 = 0
x0 = (3, 0)
x1 = (2, 0)

Воспользуемся WolframAlpha для проверки значений:

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Решение кубических уравнений

Кубическим уравнением называется уравнение третьего порядка, которое имеет вид

Кубическое уравнение всегда имеет 3 корня, которые могут быть как вещественными, так и комплексными. Для решения кубических уравнений используется метод Виета-Кардано.

Формулы Кардано и Виета требуют применения специальных функций, и в том случае, когда требуется провести большую серию вычислений корней кубического уравнения с не слишком сильно меняющимися коэффициентами, более быстрым алгоритмом является использование метода Ньютона или других итерационных методов (с нахождением начального приближения по формулам Кардано-Виета), о которых мы поговорим дальше.

Рассмотрим в качестве примера следующие кубические уравнения:

• x^3 — 6x^2 + 11x — 6 = 0
• x^3 — 6x^2 + 11x + 6 = 0

Напишем программу для решения кубических уравнений с помощью метода Виета-Кардано:

Напишем программу для тестирования метода:

x^3 — 6x^2 + 11x — 6 = 0
x0 = (1, 0)
x1 = (3, 0)
x2 = (2, 0)

x^3 — 6x^2 + 11x + 6 = 0
x0 = (-0,434841368216901, 0)
x1 = (3,21742068410845, 1,85643189109788)
x2 = (3,21742068410845, -1,85643189109788)

Решим эти же уравнения с помощью WolframAlpha.

Видео:Задача #19 Найдите корни кубического уравнения.Скачать

Решение биквадратных уравнений

Биквадратное уравнение — уравнение четвёртой степени вида

где a,b,c — заданные комплексные числа и a != 0. Подстановкой y = x 2 сводится к квадратному уравнению относительно y. Такой переход от одной неизвестной величины к другой называется методом замены неизвестных.

Рассмотрим в качестве примера кубические уравнения:

• 5x^4 — 10x^2 + 200 = 0
• x^4 — 8x^2 + 16 = 0
• x^4 — 5x^2 + 6 = 0

Таким образом немного модифицируем первую функцию для решения биквадратных уравнений:

Напшем программу для тестирования метода:

На выходе получим такие результаты:

5x^4 — 10x^2 + 200 = 0
x0 = (1,63164875514566, -1,91370783040891)
x1 = (-1,63164875514566, 1,91370783040891)
x2 = (1,63164875514566, 1,91370783040891)
x3 = (-1,63164875514566, -1,91370783040891)

x^4 — 8x^2 + 16 = 0
x0 = (2, 0)
x1 = (-2, 0)
x2 = (2, 0)
x3 = (-2, 0)

x^4 — 5x^2 + 6 = 0
x0 = (1,73205080756888, 0)
x1 = (-1,73205080756888, 0)
x2 = (1,4142135623731, 0)
x3 = (-1,4142135623731, 0)

По ссылкам раз, два, три можно убедиться в правильности решений.

Видео:Математика это не ИсламСкачать

Полное решение кубического уравнения (формула Кардано)

Необходимо решить кубическое уравнение с действительными коэффициентами: ax 3 + bx 2 + cx + d = 0 .

По основной теореме алгебры оно имеет три корня (4 различных типа).

Формула была украдена у Тартальи и опубликована Джероламо Кардано (тем самым изобретателем карданного вала) в книге «Великое искусство» в 1545 году. Описание алгоритма доступно в Интернете, однако программная реализация имеет некоторые нюансы, связанные с необходимостью анализа исходных данных. Вот что получилось:

Входными параметрами метода являются коэффициенты a, b, c, d; по ссылке возвращается тип корней (tip=1,2,3,4) и их значения (p1,p2,p3):

Для типа 1 (tip=1) имеется один действительный и два комплексных корня: x1=p1; x2=p2+i*p3; x3=p2-i*p3, где i — мнимая единица.
Тип 2 — три различных действительных корня, тип 3 — один отличающийся и два кратных действительных корня, тип 4 — три кратных действительных корня, для всех типов (tip=2,3,4) x1=p1, x2=p2, x3=p3.
Если кубическое уравнение является характеристическим уравнением исходного линейного дифференциального уравнения 3 степени, то для его решения важно знать именно тип решения (tip).

Для тестирования метода используйте следующую программу:

Минимальный набор тестов:
a, b, c, d:
187.5, 50, 10, 1 -> тип 1
1, 6, 3, -10 -> тип 2
1, 12, 36, 32 -> тип 3
3, -9, 9, -3 -> тип 4

New: Наш Чат

В чате вы можете обсудить любые вопросы, идеи, поделиться опытом или связаться с администраторами.

🎥 Видео

Теорема БезуСкачать

Самый простой способ решить кубическое уравнениеСкачать

ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать

Алгоритмы. Нахождение корней уравнения методом хордСкачать

Нахождение иррациональных корней кубических уравнений. Быстрый способ решения кубических уравнений.Скачать

ФОРМУЛА КАРДАНО-ТАРТАЛЬЯ + РЕКЛАМА МФТИ!!!Скачать

Решение кубического уравнения общего вида, используя комплексные числа, по формуле Кардано!Скачать

Формула Кардано. Решение уравнений третьей степени.Скачать

Графический метод решения задачи линейного программирования (ЗЛП)Скачать

Алгебра. Кубический корень.Скачать

Формула Кардано - Тартальи// Почему выглядит именно так?Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Теорема Виета для уравнений высших степеней. Рациональные уравнения Часть 4 из 4Скачать