Найти корни квадратного уравнения и вывести их на экран, если они есть. Если корней нет, то вывести сообщение об этом. Конкретное квадратное уравнение определяется коэффициентами a , b , c , которые вводит пользователь.
Квадратное уравнение имеет вид ax 2 + bx + c = 0 . Коэффициенты a , b и c — это конкретные числа, а x надо найти, решив уравнение.
- Вычислить дискриминант по формуле d = b 2 — 4ac .
- Если дискриминант больше нуля, то вычислить два корня уравнения:
x1 = (-b+√d) / 2a
x2 = (-b-√d) / 2a - Если дискриминант равен нулю, то вычислить только один корень (второй будет равен ему).
- Если дискриминант отрицателен, то вывести сообщение, что корней нет.
Видео:MIT App Inventor. Создание приложения для нахождения корней квадратного уравненияСкачать

Pascal
квадратное уравнение паскаль
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Язык Си
Ключ -lm при компиляции gcc.
Видео:34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Python
Видео:Нахождение корней квадратного уравненияСкачать

КуМир
Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Basic-256
- Total 0
- 0
- 0
- 0
- 0
квадратное уравнение паскаль
var
a,b,c,d,x1,x2: real;
begin
write(‘a=’); readln(a);
write(‘b=’); readln(b);
write(‘c=’); readln(c);
d := b*b — 4*a*c;
if d > 0 then begin
x1 := (-b + sqrt(d)) / (2*a);
x2 := (-b — sqrt(d)) / (2*a);
writeln(‘x1=’,x1:3:2,’; x2=’,x2:3:2);
end
else
if d = 0 then begin
x1 := (-b) / (2*a);
writeln(‘x=’,x1:5:2);
end
else
writeln(‘Корней нет’);
end.
main() <
float a,b,c,d,x1,x2;
printf(«a=»); scanf(«%f»,&a);
printf(«b=»); scanf(«%f»,&b);
printf(«c=»); scanf(«%f»,&c);
d = b*b — 4*a*c;
if (d>0) <
x1 = (-b + sqrt(d)) / (2*a);
x2 = (-b — sqrt(d)) / (2*a);
printf(«x1=%.2f; x2=%.2f», x1, x2);
>
else
if (d = 0) <
x1 = -b / (2*a);
printf(«x1=%.2f; x2=%.2f», x1, x2);
>
else printf(«Корней нет.»);
printf(«n»);
>
Ключ -lm при компиляции gcc.
python квадратное уравнение
print(«Введите коэффициенты для квадратного уравнения (ax^2 + bx + c = 0):»)
a = float(input(«a = «))
b = float(input(«b = «))
c = float(input(«c = «))
discr = b**2 — 4 * a * c;
print(«Дискриминант D = %.2f» % discr)
if discr > 0:
import math
x1 = (-b + math.sqrt(discr)) / (2 * a)
x2 = (-b — math.sqrt(discr)) / (2 * a)
print(«x1 = %.2f nx2 = %.2f» % (x1, x2))
elif discr == 0:
x = -b / (2 * a)
print(«x = %.2f» % x)
else:
print(«Корней нет»)
input «a = «, a
input «b = «, b
input «c = «, c
d = b^2 — 4*a*c
if d > 0 then
x1 = (-b + sqrt(d)) / (2*a)
x2 = (-b — sqrt(d)) / (2*a)
print «x1 = » + x1 + «, x2 = » + x2
else
if d = 0 then
x = -b / (2*a)
print «x = » + x
else
print «Корней нет»
endif
endif
Команда decimal указывает сколько знаков после запятой следует выводить.
Видео:Составьте квадратное уравнение, корнями которого являются числаСкачать

Один из методов решения квадратных уравнений
Алгоритм решения данной задачи сначала должен быть представлен в виде словесного описания или графически в виде блок-схемы. Алгоритм вычисления корней квадратного уравнения может быть представлен в виде блок-схем, изображенных на рисунках, отображающих основные элементы блок-схем и алгоритм вычисления корней квадратного уравнения:
Изображение алгоритма в виде блок-схемы позволяет наглядно представить последовательность действий, необходимых для решения поставленной задачи, убедиться самому программисту в правильности понимания поставленной задачи.
После разработки алгоритма решения задачи и представления его в виде блок-схемы можно перейти к написанию программы – последовательности инструкций на выбранном языке программирования, соответствующей разработанному алгоритму. Например, ниже приведен фрагмент программы решения квадратного уравнения, соответствующий приведенному выше алгоритму, составленному на языке Visual Basic.
procedure SqRoot(Editi,Edit2,Edit3:tEdit;Label2:tLabel);
var
a,b,c:real;
d:real;
xl,x2:real;
begin
a:=StrToFloat(Editl.text);
b:=StrToFloat(Edit2.text);
с:=StrToFloat(Edj.t3.text);
d:=Sqr(b)-4*a*c;
if d=0 then begin
Label2.color:=clRed;
Label2.font.color:=clRed;
Label2.caption:=’Дискриминант меньше нуля.’+#13+
‘Уравнение не имеет корней.’ end else
begin
х1:=(-b+Sqrt(d))/(2*a);
x2:=(-b-Sqrt(d))/(2*а);
Label2.font.color:=clBlack;
Label 2.caption=’Корни уравнения:’ +#13+’xl=1+FloatToStr(xl)
+#13+’x2=’+FloatToStr(x2);
end;
end.
Но программа, написанная на языке программирования, состоит из инструкций, понятных человеку, но не понятных процессору компьютера. Поэтому чтобы процессор смог выполнить работу в соответствии с инструкциями исходной программы, она должна быть переведена на язык команд процессора, то есть машинный язык. Задачу преобразования исходной программы в машинный код выполняет специальная программа — компилятор. Помимо преобразования исходной программы в машинную, компилятор выполняет проверку правильности записи инструкций исходной программы, т. е. осуществляет синтаксический анализ.
Компилятор создает исполняемую программу только в том случае, если в тексте исходной программы нет синтаксических ошибок. Однако генерация исполняемой программы машинного кода свидетельствует только об отсутствии в тексте программы синтаксических ошибок. Убедиться в правильности работы программы можно только во время ее тестирования – пробных запусках программы и при анализе полученных результатов. Например, если в программе нахождения корней квадратного уравнения допущена ошибка в записи выражения вычисления дискриминанта, то даже если это выражение будет синтаксически верно, программа выдаст неверные значения корней.
Решение квадратных уравнений средствами Visual Basic
Задача: Дано квадратное уравнение общего вида: ax 2 +bx+c=0. Ввести в память компьютера числовые коэффициенты: a, b, c, выполнить необходимый анализ введенной информации согласно известному из курса средней школы алгоритму решения квадратного уравнения: найти дискриминант d=b 2 -4ac и, проанализировав его знак, найти все действительные корни, если знак дискриминанта положительный, или сообщить о том, что действительных корней нет, если знак дискриминанта отрицательный.
Начать составление проекта решения данной задачи необходимо с ответа на вопрос: что нужно поместить на форму Form1?
Поместим на форму две кнопки: CommandButton1 и CommandButton2.
Для этого нужно воспользоваться Панелью элементов (объектов) управления General, которая расположена в левой части основного окна компилятора Visual Basic.
Первая кнопка CommandButton1 предназначается для начала работы программы согласно следующему алгоритму:
- ввод коэффициентов исходного уравнения a, b, c;
- расчет дискриминанта d=b 2 — 4ac;
- анализ знака дискриминанта, вычисление корней уравнения и вывод их на форму, если знак дискриминанта d>0 (положительный);
- вывод сообщения: «Решений нет», если знак дискриминанта d 2 -5x+6=0.
Далее рассмотрим процесс решения второго квадратного уравнения: 10x 2 +5x+200=0.
В окне InputBox вводим значение первого коэффициента уравнения a=10.
Ввод первого коэффициента a завершается нажатием кнопки Ok.
Аналогично в окне InputBox вводим значение второго коэффициента уравнения b=5.
Ввод второго коэффициента b так же завершается нажатием соответствующей кнопки Ok.
Наконец, в окне InputBox вводим значение третьего коэффициента нового уравнения c=200.
Ввод третьего коэффициента c так же завершается нажатием соответствующей кнопки Ok.
После этого программа, проанализировав полученную информацию, должна выдать в окне формы соответствующее сообщение о том, что данное уравнение не имеет решений.
И, наконец, рассмотрим процесс решения третьего квадратного уравнения: x 2 -8x+16=0.
Это уравнение имеет двукратный корень, так как его дискриминант d=0. Как и в двух предыдущих случаях, вводим коэффициенты квадратного уравнения. Первым вводим коэффициент a=1.
Далее вводим второй коэффициент уравнения b= –8.
Третий коэффициент уравнения c=16 вводим в последнюю очередь.
В итоге мы должны увидеть правильное решение третьего квадратного уравнения. Действительно последнее уравнение имеет два одинаковых корня.
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Ветвящийся алгоритм решения квадратного уравнения
Задание. Необходимо решить квадратное уравнение:
где a=2; b=-5; c=2. Решение. Представим алгоритм решения квадратного уравнения в словесной форме.
1. Вычислить дискриминант квадратного уравнения:
2. Если D 0, то уравнение имеет два корня:
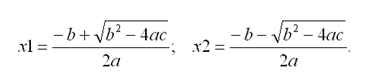
Таким образом, для решения квадратного уравнения необходимо использовать разветвляющийся алгоритм.
Для ввода исходных данных и вывода результатов вычисления можно использовать пользовательскую форму, например, как показано на рис. 1.
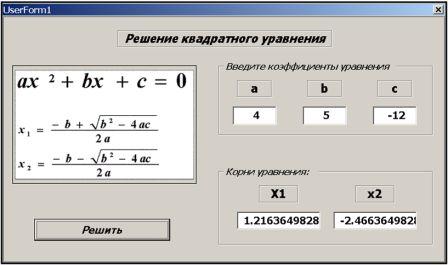
Рисунок 1
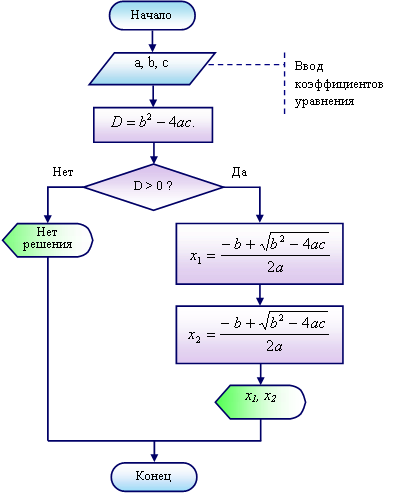
Рисунок 2
Программа вычисления корней квадратного уравнения запускается нажатием на кнопку «Решить».
Эта программа имеет следующий вид:
Private Sub CommandButton1_Click()
a = TextBox1
b = TextBox2
c = TextBox3
d = (b ^ 2) — (4 * a * c) ‘ дискриминант
If d <!—
🌟 Видео
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Квадратный корень. 8 класс.Скачать

Решение биквадратных уравнений. 8 класс.Скачать

0.Блок схема. 8 классСкачать

Программа, определяющая корни квадратного уравнения. Язык программирования Python.Скачать

Дискриминант. Условия нахождения корней квадратного уравнения.Скачать

Быстрый способ решения квадратного уравненияСкачать

Метод выделения полного квадрата. 8 класс.Скачать

Программа для решения корней квадратного уравнения с использованием дискриминанта на языке ПаскальСкачать
Комплексные корни квадратного уравненияСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Формула корней квадратного уравнения – 8 класс алгебраСкачать

Как решать квадратные уравнения без дискриминантаСкачать











