Элементы квантовой механики
Корпускулярно-волновой дуализм свойств частиц вещества.
§1 Волны де Бройля
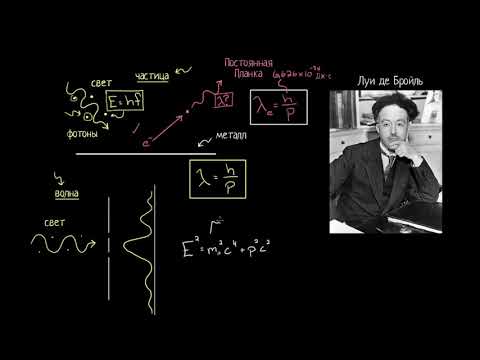
В 1924г. Луи де Бройль (французский физик) пришел к выводу, что двойственность света должна быть распространена и на частицы вещества — электроны. Гипотеза де Бройля заключалась в том, что электрон, корпускулярные свойства которого (заряд, масса) изучаются давно, имеет еще и волновые свойства, т.е. при определенных условиях ведет себя как волна.
Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов.
Идея де Бройля состояла в том, что это соотношение имеет универсальный характер, справедливый для любых волновых процессов. Любой частице, обладающей импульсом р, соответствует волна, длина которой вычисляется по формуле де Бройля.

p = mv — импульс частицы, h — постоянная Планка.



Дальнейшее подтверждение гипотезы де Бройля в опытах Л.С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (Е » 50 кэВ) через фольгу из различных металлов. Затем была обнаружена дифракция нейтронов, протонов, атомных пучков и молекулярных пучков. Появились новые методы исследования вещества — нейтронография и электронография и возникла электронная оптика.
Макротела также должны обладать всеми свойствами ( m = 1кг, следовательно, l = 6 . 6 2 · 1 0 — 3 1 м — невозможно обнаружить современными методами — поэтому макротела рассматриваются только как корпускулы).
§2 Свойства волн де Бройля
- Пусть частица массы m движется со скоростью v . Тогда фазовая скорость волн де Бройля

Т.к. c > v , то фазовая скорость волн де Бройля больше скорости света в вакууме ( v ф может быть больше и может быть менше с, в отличие от групповой ).
- следовательно, групповая скорость волн де Бройля равна скорости движения частицы.
т.е. групповая скорость равная скорости света.
- Волны де Бройля испытывают дисперсию. Подставив
в
получим, что vф = f (λ). Из-за наличия дисперсии волны де Бройля нельзя представить в виде волнового пакета, т.к. он мгновенно “ расплывется “ (исчезнет) за время 10 -26 с.
§3 Соотношение неопределенностей Гейзенберга
Микрочастицы в одних случаях проявляют себя как волны, в других как корпускулы. К ним не применимы законы классической физики частиц и волн. В квантовой физике доказывается, что к микрочастице нельзя применять понятие траектории, но можно сказать, что частица находится в данном объеме пространства с некоторой вероятностью Р. Уменьшая объем, мы будем уменьшать вероятность обнаружить частицу в нем. Вероятностное описание траектории (или положения) частицы приводит к тому, что импульс и, следовательно, скорость частицы может быть определена с какой-то определенной точностью.
Далее, нельзя говорить о длине волны в данной точке пространства и отсюда следует, что если мы точно задаем координату Х, то мы ничего не сможем сказать о импульсе частицы, т.к. 
Соотношение неопределенностей Гейзенберга устанавливает границу в одновременном определении точности канонически сопряженных величин, к которым относятся координата и импульс, энергия и время.
Соотношение неопределенностей Гейзенберга: произведение неопределенностей значений двух сопряженных величин не может быть по порядку величины меньше постоянной Планка h
( иногда записывают 
Таким образом. для микрочастицы не существует состояний, в которых её координата и импульс имели бы одновременно точные значения. Чем меньше неопределенность одной величины, тем больше неопределенность другой.
Соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.
следовательно, чем больше m , тем меньше неопределенности в определении координаты и скорости. При m = 10 -12 кг , ? = 10 -6 и Δ x = 1% ?, Δv = 6,62·10 -14 м/с, т.е. не будет сказываться при всех скоростях, с которыми пылинки могут двигаться, т.е. для макротел их волновые свойства не играют никакой роли.
Пусть электрон движется в атоме водорода. Допустим Δ x » 1 0 -10 м (порядка размеров атома, т.е. электрон принадлежит данному атому). Тогда
Δv = 7,27· 1 0 6 м/с. По классической механике при движении по радиусу r » 0 , 5 · 1 0 — 1 0 м v = 2,3·10 -6 м/с. Т.е. неопределенность скорости на порядок больше величины скорости, следовательно, нельзя применять законы классической механики к микромиру.
Из соотношения 

§4 Волновая функция и ее физический смысл
Дифракционная картина, наблюдающаяся для микрочастиц, характеризуется неодинаковым распределением потоков микрочастиц в различных направлениях — имеются минимумы и максимумы в других направлениях. Наличие максимумов в дифракционной картине означает, что в этих направлениях распределяются волны де Бройля с наибольшей интенсивностью. А интенсивность будет максимальной, если в этом направлении распространяется максимальное число частиц. Т.е. дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности в распределении частиц: где интенсивность волны де Бройля максимальная, там и частиц больше.
Волны де Бройля в квантовой механике рассматриваются как волны вероятности, т.е. вероятность обнаружить частицу в различных точках пространства меняется по волновому закону ( т.е.
е — iωt ). Но для некоторых точек пространства такая вероятность будет отрицательной (т.е. частица не попадает в эту область). М. Борн ( немецкий физик ) предположил, что по волновому закону меняется не сама вероятность, а амплитуда вероятности, которую также называют волновой функцией или y -функцией (пси — функцией).
Волновая функция — функция координат и времени.
Квадрат модуля пси-функции определяет вероятность того, что частица будет обнаружена в пределах объема dV — физический смысл имеет не сама пси-функция, а квадрат ее модуля.
Ψ * — функция комплексно сопряженная с Ψ
Если частица находится в конечном объеме V , то возможность обнаружить ее в этом объеме равна 1, (достоверное событие)
Р = 1 Þ
В квантовой механике принимается, что Ψ и АΨ, где А = const , описывают одно и то же состояние частицы. Следовательно,
интеграл по 
y — функция должна быть
1) конечной (так как Р не может быть больше1),
2) однозначной (нельзя обнаружить частицу при неизменных условиях с вероятностью допустим 0,01 и 0,9, так как вероятность должна быть однозначной).
- непрерывной (следует из неприрывности пространства. Всегда имеется вероятность обнаружить частицу в разных точках пространства, но для разных точек она будет разная),
- Волновая функция удовлетворяет принципусуперпозиции: если система может находится в различных состояниях, описываемых волновыми функциями y 1 , y 2 . y n , то она может находится в состоянии y , описываемой линейной комбинаций этих функций:
С n ( n =1,2. ) — любые числа.
С помощью волновой функции вычисляются средние значения любой физической величины частицы
§5 Уравнение Шредингера
Уравнение Шредингера, как и другие основные уравнения физики (уравнения Ньютона, Максвелла), не выводится, а постулируется. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем, что все вытекающие из него следствия точно согласуются с экспериментальными данными.

— Временное уравнение Шредингера.


Ψ( y , z , t ) — искомая функция
Если силовое поле, в котором движется частица, стационарно (т.е. не изменяется с течением времени), то функция U не зависит от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера (т.е. Ψ — функция) может быть представлено в виде произведения двух сомножителей — один зависит только от координат, другой — только от времени:

Е — полная энергия частицы, постоянная в случае стационарного поля.

— Уравнение Шредингера для стационарных состояний.
Имеется бесконечно много решений. Посредством наложения граничных условий отбирают решения, имеющие физический смысл.
волновые функции должны быть регулярными, т.е.
Решения, удовлетворяющие уравнению Шредингера, называются собственными функциями, а соответствующие им значения энергии — собственными значениями энергии. Совокупность собственных значений называется спектром величины. Если Е n принимает дискретные значения, то спектр — дискретный, если непрерывные — сплошной или непрерывный.
§6 Движение свободной частицы
Частица называется свободной, если на нее не действуют силовые поля, т.е. U = 0.
Уравнение Шредингера для стационарных состояний в этом случае:
И собственные значения энергии:


Т.к. k может принимать любые значения, то, следовательно, и Е принимает любые значения, т.е. энергетический спектр будет сплошным.
Временная волновая функция

т.е. представляет плоскую монохромную волну де Бройля.
§7 Частица в “потенциальной яме” прямоугольной формы.
Квантование энергии.
Найдем собственные значения энергии и соответствующие им собственные функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме. Предположим что, частица может двигаться только вдоль оси x . Пусть движение ограничено непроницаемыми для частицы стенками x = 0, и x = ?. Потенциальная энергия U имеет вид:

Уравнение Шредингера для стационарных состояний для одномерной задачи
За пределы потенциальной ямы частица попасть не сможет, поэтому вероятность обнаружения частицы вне ямы равна 0.Следовательно, и Ψ за пределами ямы равна 0 .Из условий непрерывности следует, что Ψ = 0 и на границах ямы т.е.
В пределах ямы (0 £ x £ l ) U = 0 и уравнение Шредингера.
введя 

из граничных условий следует
Из граничного условия

Энергия Е n частицы в «потенциальной яме» с бесконечно высокими стенками принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Е n называются уровнями энергии, а число n , определяющее энергические уровни частицы, называется главным квантовым числом. Т.е. частицы в «потенциальной яме» могут находиться только на определенном энергетическом уровне Е n (или находятся в квантовом состоянии n )
Собственные функции:
А найдем из усилия нормировки

Энергетический интервал между соседними уровнями энергии:
При n = 1 имеет наименьшую энергию отличную от нуля
Наличие минимума энергии следует из соотношения неопределенностей, т.к.
C ростом n расстояние между уровнями уменьшается и при n ® ¥ Е n практически непрерывны, т.е. дискретность сглаживается, т.е. выполняется принцип соответствия Бора: при больших значениях квантовых чисел законы квантовой механики переходят в законы классической физики.
Общая трактовка принципа соответствия: всякая новая, более общая теория является развитием классической, не отвергает ее полностью, а включает в себя классическую, указывая границы её применимости.
§ 8 Туннельный эффект.
Прохождение частицы через потенциальный барьер

Потенциальная энергия:
Уравнение Шредингера: для области 1 и 3 :
для области 2: 
Решение этих диф. уравнений;
Для 1;
Для 2;
Для 3:

Т.к. в области 3 возможно распределение только прошедшей волны, то, Þ , В3=0.
В области 2 решение зависит от соотношений Е > U или Е U . Физический интерес представляет случай Е U .
q = i b , где
Тогда решение уравнения Шредингера запишутся в виде:
Для 1;
Для 2;
Для 3:
Качественный вид функций показан на рис. 2. Из рис. 2 видно, что функция не равна нулю внутри барьера, а в 3 имеет вид волны де Бройля, если барьер не очень широк.
Явление “проникновения” частицы сквозь потенциальный барьер, называется туннельным эффектом. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы можно объяснить используя соотношения неопределенностей: неопределенность импульса D р на отрезке D x = ? составляет 

§9 Линейный гармонический осциллятор
Линейный гармонический осциллятор — система, совершающая одномерное колебательное движение под действием квазиупругой силы — является моделью для изучения колебательного движения.
В классической физике — это пружинный, физический и математический маятники. В квантовой физике — квантовый осциллятор.
Записав потенциальную энергию в виде

Уравнение Шредингера запишется в виде:
Тогда собственные значения энергии:
т.е. энергия квантового осциллятора принимает дискретные значения, т.е. квантуется. Минимальное значение 
Наличие нулевых колебаний означает, что частицы не могут упасть на дно ямы, т.к. в этом случае был бы точно определен ее импульс p = 0, D p = 0, Þ , D x = ¥ — не соответствует соотношению неопределенностей. Наличие энергии нулевых колебаний противоречит 


- Соотношение неопределенности, волновая функция, излучение и поглощение энергии
- Конспект лекции
- Волновая функция
- Уравнение Шредингера
- Решение уравнения Шредингера для свободной частицы
- Тождественность частиц. Бозоны и фермионы. Принцип Паули.
- Вычисление средних значений
- Излучение и поглощение энергии
- Уравнение Шрёдингера
- 💥 Видео
Видео:Гипотеза де Бройля. Соотношения неопределенностей. Уравнение Шредингера.Скачать

Соотношение неопределенности, волновая функция, излучение и поглощение энергии
Конспект лекции
Аннотация: знакомство с границами применимости классической физики, уравнением Шредингера. Традиционное изложение темы.
В первой четверти XX-го века получены экспериментальные свидетельства двойственности свойств материи: электромагнитное излучение проявляет свойства частиц (фотоэффект, комптоновское рассеяние, . ), а частицы демонстрируют волновые свойства (эффект Рамзауэра, туннельный эффект, . ).
Но свойства волн и частиц в известной степени противоположны.
| Частицы | Волны |
|---|---|
| Энергия и импульс локализованы | Переносят энергию, распределенную по фронту волны |
| Сложение по правилу: частицы + частицы => больше частиц | Интерференция лучей: больше в одном месте и меньше в другом |
| Отбрасывают резкую тень | Огибают препятствия |
| При наличии щелей частица проходит через одну из них | Проходят через любое число отверстий |
Нет подходящих образов, чтобы представить существование волновых и корпускулярных свойств у одного объекта. Нельзя все свойства волн и все свойства частиц приписать одному объекту. Необходимо внести некоторые ограничения в применении к объектам микромира понятий классической физики. Корпускулярно-волновая двойственность свойств частиц, изучаемых в квантовой механике, приводит к тому, что в ряде случаев оказывается невозможным, в классическом смысле, одновременно характеризовать частицу ее положением в пространстве (координатами) и скоростью (или импульсом). В 1927 году немецкий физик Вернер Гейзенберг сформулировал принцип неопределенности, названный теперь его именем. Он может быть записан в следующем виде

Здесь Δx — неопределенность координаты x, Δp — неопределенность импульса, ħ — постоянная Планка, деленная на 2π (h = 6.62·10 -34 Дж·с). Выражение (1) следует понимать так, что если мы точно задаем координату частицы (Δx → 0), то ничего не можем сказать о величине импульса (Δp → ∞). Одновременно точно задать координату и импульс микрочастицы невозможно. Для иллюстрации рассмотрим опыт по дифракции электронов на щели. Прямой опыт Йенсона (см. лекцию) показал, что за щелью распределение интенсивности электронов будет иметь вид, показанный на рис.1. 
Отклонение электрона от первоначального направления означает получение им приращения импульса Δp. Ширина щели служит мерой неопределенности положения электрона (электрон проник в щель, в какой точке щели это произошло, неизвестно). Из опыта известно, что при уменьшении ширины щели дифракционная картина уширяется. Т.е., если Δx уменьшается, Δp растет, как это предсказывает соотношение (1).
Принцип неопределенности не мешает нам с любой желаемой точностью измерить каждую из величин, входящих в соотношение. Он утверждает лишь, что мы не в состоянии достоверно узнать и то, и другое одновременно. Неравенства (1) и (2) представляют собой ограничения применимости понятий классической механики.
Оценим количественную сторону ограничений на трех примерах.
- Молекула в стакане.
Массы молекул имеют порядок 10 -27 кг. Пусть стакан имеет размер
10 -1 м. Эту величину возьмем в качестве неопределенности координаты Δx. Тогда для неопределенности скорости получим

Чрезвычайно малое значение Δv в сравнение со скоростью молекул (при комнатной температуре порядка 500 м/с) приводит к выводу об отсутствии ограничений на классическое рассмотрение движения молекул в этом случае.
Электрон в атоме.
10 -30 кг, размер атома
10 -10 м. Для неопределенности скорости получим

И поскольку эта величина Δv сравнима со скоростью электронов в атоме, соотношение неопределенностей играет решающую роль, игнорировать волновые свойства электрона никак нельзя.
Луч осциллографа.
Скажутся ли волновые свойства электрона на работе осциллографа? Пусть радиус луча на экране очень качественного осциллографа равен r = 10 мкм, длина трубки L
10 -1 м. Тогда относительное изменение импульса Δp/p = r/L = 10 -4 . Импульс электрона определим, задав напряжение на трубке U, равным 10 кВ

Неопределенность импульса тогдаΔp
6·10 -27 , а неопределенность координаты
что существенно меньше размера пятна на экране. Т.е. пользоваться осциллографом можно, не задумываясь о волновых свойствах электронов.
Приведем один пример использования соотношения неопределенностей для оценки физических величин. Исходим из того, что неопределенность, например, импульса — это минимальное значение импульса, которое что-то значит.
Покажем, что в существующих ядрах не могут находиться электроны. За неопределенность координаты возьмем радиус ядра r, тогда
Размеры ядер имеют порядок 10 -14 м, электрон с таким импульсом — ультрарелятивистский, его энергия много больше энергии покоя, и последней можно пренебречь в оценках. Имеем E = p·c (как для фотонов). Для того чтобы электрон находился в ядре, его кинетическая энергия должна быть меньше потенциальной энергии (энергии взаимодействия с заряженным шаром, которым представляем ядро). Получаем
Ядер с таким большим атомным номером не существует. Точное решение задачи с нахождением волновой функции показывает отсутствие связанного состояния для электрона в потенциальной яме, которой представляется ядро.
Другая важная пара связанных физических величин – энергия Е и время t. Соотношение неопределённостей для них имеет вид

Если под величиной Δt понимать среднее время жизни атома в возбужденном состоянии, то энергия этого состояния определена с точностьюΔE. В основном состоянии атом может находиться без внешних воздействий бесконечно долгое время: Δt = ∞. Тогда ΔE = 0, то есть в основном состоянии энергия атома является строго определенной величиной. Однако каждый возбужденный уровень энергии имеет конечную ширину, которая определяется временем жизни атома в этом состоянии. Вследствие этого длина волны испускаемого кванта при переходе из возбужденного состояния не будет однозначной, спектральная линия излучающего атома имеет конечную ширину. Говорят о естественной ширине линии. Ширина спектральной линии определяется шириной уровней энергии, между которыми происходит переход. Обычно ширина уровней энергии очень мала. Например, для переходов с излучением в видимой части спектра (время жизни атома в возбужденном состоянии
Соотношение (2) допускает рождение на короткое время с последующим исчезновением частиц (их называют виртуальными (возможными) частицами). Их время жизни очень мало — порядка 10 -21 — 10 -24 с. Это объясняет, почему в вакууме постоянно присутствуют кванты различных полей. Отдельные виртуальные частицы нельзя обнаружить в принципе, но их суммарное воздействие на обычные микрочастицы обнаруживается экспериментально. В опыте У.Лэмба и Р.Ризерфорда (1947 г.) при исследовании спин-орбитального расщепления (см. лекцию) 2p уровня атома водорода обнаружено не только ожидаемое расщепление энергий состояний 2p3/2 и 2p1/2, но и отличие энергий 2s1/2 и 2p1/2 состояний. Это отличие обусловлено, как выяснилось позднее, во-первых, испусканием и поглощением связанным электроном виртуальных фотонов, что приводит к изменению эффективной массы электрона и возникновению у него аномального магнитного момента, и, во-вторых, возможностью виртуального рождения и аннигиляции в вакууме электронно-позитронных пар, что искажает кулоновский потенциал ядра. Лэмбовский сдвиг оказался первым физическим эффектом, на котором подтвердилась правильность квантовой электродинамики.
Видео:Урок 455. Уравнение ШрёдингераСкачать

Волновая функция
Наличие волновых свойств у микрочастицы показывает, что ей (микрочастице) следует сопоставить некоторое волновое поле (аналог знакомых нам электрического, магнитного, гравитационного полей). Амплитуду этого волнового поля, зависящую от координат и времени, принято называть волновой функцией 
величина 
Вспомним опыт с пропусканием электронов через щель. Куда попадет данный конкретный электрон — дело случая. После пропускания малого числа электронов картина похожа на мишень плохого стрелка. Поведение электрона должно описываться некоторой вероятностной функцией. И эта функция должна быть связана со свойствами волнового поля, т.к. итог большого числа попаданий электронов — вполне четкая картина дифракционных полос. Совместить случайный характер попадания электрона в данное место с его волновыми свойствами можно, лишь допустив, что вероятность попадания электрона в данную точку пропорциональна интенсивности волнового поля, т.е. квадрату амплитуды |Ψ| 2 . |Ψ| 2 имеет смысл плотности вероятности. С помощью волновой функции можно рассчитать все измеряемые физические характеристики системы частиц. Например, среднее расстояние электрона от ядра
Свойства волновой функции:
- самое главное — сама амплитуда Ψ(x,y,z,t) непосредственного физического смысла не имеет; только |Ψ| 2 — плотность вероятности;
- волновая функция может быть комплексной (так чаще всего и бывает);
- умножение волновой функции на постоянную величину не изменяет физического состояния частицы, которая она описывает (распределение вероятности в пространстве и во времени не изменится; во сколько раз частицу чаще можно встретить в одной точке, чем в другой, во столько же раз и после умножения);
- волновая функция должна быть непрерывной и однозначной;
- непрерывной должна быть и первая производная по координате, так как через нее определяется импульс частицы;
- волновая функция не должна обращаться в бесконечность;
- обычно волновую функцию нормируют так ,что
т.е. вероятности достоверного события.
Видео:Как понять принцип неопределённости Гейзенберга? [Veritasium]Скачать
![Как понять принцип неопределённости Гейзенберга? [Veritasium]](https://i.ytimg.com/vi/ZzCGTLJblkw/0.jpg)
Уравнение Шредингера
Уравнение, решением которого является волновая функция, получено австрийским физиком Э.Шредингером
- m — масса частицы;
- Ψ(x,y,z,t) — волновая функция;
- ħ — постоянная Планка, деленная на π2;
— оператор Лапласа;
- U(x,y,z,t) — потенциальная энергия;
- i — мнимая единица.
Это уравнение применимо только для нерелятивистских частиц, у которых масса не зависит от скорости.
Для многих задач уравнение Шредингера можно упростить, исключив зависимость от времени. Это так называемые стационарные задачи. Пусть потенциальная энергия зависит только от координат U = U(x,y,z). Будем искать решение в виде произведения двух функций, зависящих одна от координат, а другая от времени: Ψ(x,y,z,t) = ψ(x,y,z)·φ(t). Поставим это выражение в уравнение и вынесем из-под знаков дифференцирования сомножители, не зависящие от соответствующих переменных
Разделим получившееся уравнение на ψ(x,y,z)·φ(t). Теперь левая часть зависит только от координат, а правая от времени. Поскольку обе части равны между собой, то остается единственная возможность: каждая из них равна одной и той же константе. Обозначим эту константу -E (E, как будет видно, — полная энергия частицы).
Теперь имеем два уравнения: первое для функции ψ(x,y,z)
Это так называемое стационарное уравнение Шредингера. Второе, которое легко решается, для временной части
Итак, для стационарного случая имеем два дифференциальных уравнения. Многочисленные эксперименты подтверждают выводы, вытекающие из решения уравнения Шредингера. На этом основана наша уверенность в справедливости этого уравнения.
В 1933г. Эрвину Шредингеру присуждена Нобелевская премия:
E RWIN S CHRODINGER for the discovery of new productive forms of atomic theory.
(за открытие новых продуктивных форм атомной теории)
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Решение уравнения Шредингера для свободной частицы
Для понимания природы явлений в микромире обычно достаточно решить одномерную задачу. Этим мы и займемся. Для свободной частицы U(x) = 0, и уравнение Шредингера имеет вид

Имеем дифференциальное уравнение второго порядка с посто39янными коэффициентами. Его решение, используя характеристическое уравнение, получаем в виде

Теперь добавим множитель φ(t), зависящий от времени (см. выше)

Если учесть, что E/ħ = ω, получили уравнение волны с фазой kx-ωt в первом слагаемом и -kx-ωt во втором. Если фазу зафиксировать, то точка с постоянной фазой движется в направлении x для первого слагаемого (x растет с увеличением t), и в противоположном для второго. Первое слагаемое описывает движение частицы в направлении x, второе — против x.
Выражение (4) однозначно, конечно и имеет смысл при любых значениях энергии E. Энергия свободной частицы может принимать любое значение, т.е. ее энергетический спектр является непрерывным.
Этой волне соответствует не зависящая от времени вероятность обнаружить частицу в данной точке пространства. Действительно, выбирая для простоты волну, распространяющуюся в положительном направлении x, имеем |Ψ| 2 = Ψ·Ψ * = |A| 2 .
И напоследок получим соотношение между импульсом p и энергией E свободной частицы. Вспоминая выражение для длины волны де Бройля, для волнового числа k получим

Возведя это выражение в квадрат и приравняв к равенству для k 2 (3), получим
что совпадает с классическим соотношением.
Видео:Квантовая физика для чайников!Скачать

Тождественность частиц. Бозоны и фермионы. Принцип Паули.
Проделаем опыт по изучению углового распределения упруго рассеянных α-частиц на ядрах углерода 12 C: α + 12 C → α + 12 C. 
Но может быть (рисунок 2б) α-частица рассеялась на угол π — θ и попадает в детектор 2. Этот процесс описывается функцией Ψ(π — θ). Детекторы 1 и 2 включены в схему совпадений, и событие считается зарегистрированным, когда в каждый детектор попадет по частице.
Можно ли сделать детектор, различающий α-частицы и ядра углерода? Отвечаем «да», и случаи 1а и 1б различны. Измеряемая величина — доля частиц, рассеянных на данный угол. В случае а) она пропорциональна |Ψ(θ)| 2 , а в случае б) — |Ψ(π — θ)| 2 . А если детектор не различает частицы (например, счетчик Гейгера), тогда вероятность опыта пропорциональна
Состояния в принципе различны и складываются вероятности.
А при рассеянии α-частиц на ядрах гелия: α + 4 He → α + 4 He (α-частица — это и есть ядро гелия!)? Тут взаимодействуют тождественные частицы, и экспериментальные результаты не согласуются с формулой (5). Полная неразличимость частиц приводит к интерференции рассеянных волн. В этом случае складываются амплитуды
Если подсчитать по этим формулам вероятности для угла θ = π/2, то вероятности 2|Ψ(π/2)| 2 и |2·Ψ(π/2)| 2 = 4·|·Ψ(π/2)| 2 отличаются в два раза. Ошибиться тут нельзя. Опыт согласуется со вторым значением: для неразличимых частиц складываются амплитуды.
А как обстоит дело с электронами? Электроны в отличие от α-частиц имеют спин (собственный момент количества движения), который может иметь два направления. Если спины взаимодействующих электронов направлены одинаково, то это тождественные частицы, но ни (5), ни (6) неверно. Для них складываются амплитуды в противофазе:
Если спины электронов имеют противоположные направления, детектором можно определить, какой электрон попал в детектор, и складываются вероятности (5).
Приходим к выводу: тождественность микрочастиц существенна при описании взаимодействия этих частиц.
Электроны тождественны, и перестановка двух любых экспериментально обнаружена быть не может: возможны переходы, ведущие к неразличимым экспериментально состояниям.
| макрофизика | физика микрочастиц |
|---|---|
| можно пронумеровать частицы, наблюдать за движением определенной | понятие траектории не имеет смысла, теряет смысл и различие частиц. Обозначим волновую функцию, описывающую состояние двух частиц, через Ψ(x1,x2). Здесь x1 — координата первой частицы, x2 — второй. Подействуем на эту функцию оператором перестановки двух частиц местами Но начальное и конечное состояния ввиду тождественности частиц неразличимы, и поэтому волновые функции могут отличаться только постоянным сомножителем. Подействуем этим оператором еще раз и вернемся к исходной волновой функции Получаем a = ± 1. Волновые функции либо меняют знак при перестановке частиц либо нет Спины фермионов полуцелые: 1/2ħ, 3/2ħ. Для фермионов действует принцип Паули: в одном и том же квантовом состоянии не может быть одновременно более одного фермиона, например, электрона. Это утверждение впервые было сформулировано Вольфгангом Паули в 1925 г. Полное обобщённое доказательство этого принципа было им сделано в 1940 г. в рамках квантовой теории поля. Определенное квантовое состояние задается набором квантовых чисел. Например, для атома водорода это четыре числа. |
В 1945г. Вольфгангу Паули присуждена Нобелевская премия:
W OLFGANG P AULI for the discovery of the Exclusion Principle, also called the Pauli Principle.
(за открытие принципа запрета, названного принципом Паули)
Видео:Что такое принцип неопределенности ГейзенбергаСкачать

Вычисление средних значений
Если известна волновая функция Ψ(x), то можно вычислить значение физических величин, характеризующих данную задачу. Как упоминалось, |Ψ(x)| 2 dx — дает долю частиц, находящихся между x и x + dx. Тогда среднее значение x
Аналогично надо поступить и любых функций координаты x. Например, среднее значение потенциальной энергии U(x) равно
По-другому вычисляется средняя кинетическая энергия, которая зависит не от координаты x, а от импульса. Приведем формулу
Можно проверить последнее выражение для частного случая n = 1 в прямоугольной бесконечно глубокой потенциальной яме
что совпадает со значением полной энергии E в основном состоянии, т.к. потенциальная энергия U полагалась равной нулю.
Видео:Соотношение неопределенностей Гейзенберга за 2,5 минутыСкачать

Излучение и поглощение энергии
Чтобы выяснить, излучает ли система, содержащая заряженную частицу, надо вычислить среднее значение координаты. Если среднее значение x колеблется с частотой ν, то согласно законам электродинамики надо ожидать испускания или поглощения излучения такой частоты.
Используем волновую функцию частицы в состоянии с квантовым числом n и энергией En —
Оказывается, если частица находится в определенном энергетическом состоянии, среднее значение x не зависит от времени, и излучения нет. В 1913 году Нильс Бор для объяснения закономерности линейчатого спектра атома водорода постулировал, что атомная система может находиться только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенная энергия En. В стационарных состояниях атом не излучает. Этот постулат находился в явном противоречии с классической механикой. 
Теперь рассмотрим систему, в которой есть два состояния с квантовыми числами n, m и соответствующими им энергиями En и Em (рис.3). Принцип суперпозиции в квантовой механике заключается в следующем: если квантовая система может находиться в состояниях, описываемых волновыми функциями Ψn и Ψm, то она может находиться и в состоянии, описываемом волновой функцией
где a и b — произвольные коэффициенты. Наблюдая испускание излучения при возвращении в основное состояние n, можно заключить, что система была в состоянии m (т.е. a = 0, b = 1) в какой-то момент времени. Найдем среднее значение x для функции (8).
В подынтегральном выражении слагаемые с произведениями Ψ * n·Ψn и Ψ * m·Ψm приводят, как мы видели, к стационарным значениям x и не вызывают излучение или поглощение. Поэтому нас будут интересовать перекрестные произведения
Получили, что среднее положение частицы представляет собой периодическую функцию времени, умноженную на некоторое число (определенный интеграл по x). Поэтому получаются колебания заряда, и, следовательно, излучение с частотой
Таким образом, квантовая механика объясняет существование линейчатых спектров и обосновывает вторую гениальную догадку Н.Бора: испускание или поглощение фотонов происходит только с частотами, удовлетворяющими равенству hν = Em — En.
Теперь заметим, что колебаний заряда не будет, если интеграл В (9) равен нулю
Когда это бывает? В лекции о квантовом гармоническом осцилляторе выписаны волновые функции основного и первых двух возбужденных состояний. Для перехода m = 1 → n = 0 этот интеграл (опуская постоянные коэффициенты)
т.к. под интегралом четная функция. Аналогично для перехода m = 2 → n = 1
функция под интегралом четная и интеграл нулю не равен. Переходы m = 1 → n = 0 и m = 2 → n = 1 разрешены и сопровождаются излучением кванта.
Теперь проанализируем переход m = 2 → n = 0.
т.к. под интегралом нечетная функция. Такой переход запрещен. Детальный анализ волновых функций гармонического осциллятора показывает, что возможны только переходы, при которых квантовое число обязательно меняется на единицу Δn = ±1. Это так называемое правило отбора. Для водородоподобных атомов правила отбора будут свои.
Квантовая механика объясняет основные характеристики испускания и поглощения света.
Если возникли какие-либо вопросы, напишите мне.
Видео:Урок 457. Соотношение неопределенностейСкачать

Уравнение Шрёдингера
Дуальная корпускулярно-волновая природа квантовых частиц описывается дифференциальным уравнением.
Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны — они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики — и с блеском справился с этой задачей.
Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) — в такой передаче энергии участвуют частицы — или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа — корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений — волновыми уравнениями. Все без исключения волны — волны океана, сейсмические волны горных пород, радиоволны из далеких галактик — описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.
Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица. Хотя уравнение Шрёдингера относится к области высшей математики, оно настолько важно для понимания современной физики, что я его все-таки здесь приведу — в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой ψ («пси»), является решением следующего дифференциального уравнения (ничего страшного, если оно вам не понятно; главное — примите на веру, что это уравнение свидетельствует о том, что вероятность ведёт себя как волна):
где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.
Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.
Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа современника Шрёдингера — Вернера Гейзенберга (см. Принцип неопределенности Гейзенберга), в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий — то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче преподавать.
Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч — это частица, звук — это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле — и эксперименты это вскоре показали — в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).
Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, — яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.
💥 Видео
Теория Бора. Гипотеза де Бройля. Принцип неопределенности. Уравнение Шрёдингера.Скачать

Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать

Принцип неопределённости Гейзенберга (видео 13) | Квантовая физика | ФизикаСкачать

Соотношение неопределённостей Робертсона-ШредингераСкачать

Принцип неопределённости Гейзенберга простыми словамиСкачать

17 лекция Элементы квантовой механики Соотношения неопределенностей Уравнение Шредингера КвантовыСкачать

Урок 458. Задачи на соотношение неопределенностейСкачать

Волна де Бройля (видео 4) | Квантовая физика | ФизикаСкачать
Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

Неопределенность гейзенберга | квантовая механика |Скачать






 в
в  получим, что vф = f (λ). Из-за наличия дисперсии волны де Бройля нельзя представить в виде волнового пакета, т.к. он мгновенно “ расплывется “ (исчезнет) за время 10 -26 с.
получим, что vф = f (λ). Из-за наличия дисперсии волны де Бройля нельзя представить в виде волнового пакета, т.к. он мгновенно “ расплывется “ (исчезнет) за время 10 -26 с.



















































 — оператор Лапласа;
— оператор Лапласа;




























