Согласно уравнению непрерывности дивергенция вектора плотности тока

Видео:Билет №31 "Ток смещения"Скачать

Согласно уравнению непрерывности дивергенция вектора плотности тока

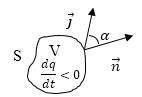
1.7.2. Уравнение непрерывности

Если внутри проводника, по которому течет электрический ток, выделить какой-то объем, ограниченный замкнутой поверхностью S (рис 1.7.2), то, согласно закону сохранения электрического заряда, суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время dt на dq = —Idt, тогда в интегральной форме можно записать:

Это соотношение называется уравнением непрерывности. Оно является, по существу, выражением закона сохранения электрического заряда.

Дифференциальная форма записи уравнения непрерывности записывается так:

В случае постоянного тока распределение зарядов в пространстве должно оставаться неизменным:

— это уравнение непрерывности для постоянного тока (в интегральной форме).

Линии j в этом случае нигде не начинаются и нигде не заканчиваются. Поле вектора j не имеет источника. В дифференциальной форме уравнение непрерывности для постоянного тока .

Видео:Билеты №12-14 "Электрический ток"Скачать

Согласно уравнению непрерывности дивергенция вектора плотности тока

Если через некоторую поверхность переносится суммарный заряд, отличный от нуля, то говорят, что через эту поверхность течет электрический ток. Ток может протекать в твердых телах, в жидкостях и в газах. Для протекания тока необходимо наличие в данном теле (или в данной среде) заряженных частиц, которые могут перемещаться в пределах всего тела. Такие частицы называются носителями тока. Ими могут быть электроны, ионы либо макроскопические частицы (например, заряженные пылинки, капельки), несущие избыточный заряд.

Направлением тока условились считать направление движения положительно заряженных частиц. Линии, вдоль которых движутся заряженные частицы, названы линиями тока. Для количественной характеристики электрического тока служат две основные величины: плотность тока и сила тока.

Плотность тока равна заряду, проходящему в единицу времени через единицу поверхности, которая перпендикулярна к линиям тока. Пусть в единице объема содержится положительных носителей тока и отрицательных.

Алгебраическая величина зарядов носителей тока равна, соответственно, и . Если под действием поля носители тока приобретают средние скорости движения и , то за единицу времени через единичную площадку пройдет положительных носителей тока, которые перенесут заряд . Аналогично отрицательные носители перенесут в противоположную сторону заряд . Таким образом, для плотности тока получается следующее выражение:

.

Или в векторном виде вектор плотности тока j определяется следующим образом

.

Если в поперечном сечении проводника выделить бесконечно малую площадку dS, перпендикулярную вектору плотности тока j, то заряд dq, проходящий через нее за время dt, равен

.

Сила тока в проводнике равна заряду, проходящему в единицу времени через полное сечение проводника. Если заряд dq, проходящий через сечение проводника за время dt, то

.

Сила тока скалярная величина. Зная вектор плотности тока в каждой точке проводника, можно выразить через него и силу тока

.

Размерность силы тока — ампер (А), единица измерения плотности тока — ампер на метр квадратный (). Если сила тока не меняется во времени, то ток, протекающий в проводнике, называют постоянным. Силу постоянного тока будем обозначать буквой I.

Рассмотрим среду, в которой течет ток, и выделим в ней замкнутую поверхность S (рис. 4.1). Для тока, выходящего в единицу времени из объема V, ограниченного поверхностью S, имеем

В силу закона сохранения заряда эта величина должна быть равна скорости убывания заряда, содержащегося в данном объеме

.
Это соотношение называют уравнением непрерывности. Учитывая, что заряд

,

получим . Преобразовав левую часть равенства по теореме о дивергенции (теореме Гаусса — Остроградского), находим

.

Таким образом в каждой точке пространства выполняется условие

,

которое является дифференциальной формой уравнения непрерывности.

Если токи постоянны, то все электрические величины не зависят от времени и в уравнении непрерывности нужно положить равным нулю. Тогда , следовательно, в случае постоянного тока вектор j не имеет источников. Это означает, что линии тока нигде не начинаются и нигде не заканчиваются, т. е. они замкнуты.

1) Что называется силой тока, плотностью тока, каковы их единицы измерения
2) Покажите, что в однородном проводнике при протекании по нему постоянного тока объемная плотность зарядов равна нулю. Какие заряды создают поле внутри проводника.
3) Может ли стационарная плотность тока j в однородном изотропном проводнике выражаться формулой , где а — константа,а x, y — декартовы координаты

Видео:Уравнение непрерывности и телеграфное уравнение | Лекция 31 | МатанализСкачать

Уравнение непрерывности

Вы будете перенаправлены на Автор24

Допустим, что в некоторой среде течет ток, выделим в этой среде гипотетическую замкнутую поверхность S (рис.1).

Исходя из закона сохранения заряда, как эмпирического факта, определим, что заряд, выходящий из объема V, который ограничен поверхностью S в единицу времени ($frac$), будет равен:

Знак минус учитывает, что если положительный заряд внутри объема уменьшается, то плотность тока направлена из объема V. Напомним, что у замкнутых объёмов положительной нормалью считается внешняя нормаль. Получается, что вектор $doverrightarrow$ направлен по внешней нормали.

Представим элементарный заряд в виде:

Из выражения (1) получим:

Под знаком интеграла в правой части стоит частная производная, так как плотность заряда может зависеть не только от времени, но и координат. В левой части (3) перейдем от поверхностного интеграла к объемному, получим:

В таком случае выражение (3) можно представить как:

Уравнение (5) должно выполняться для любого объема, следовательно:

Выражение (6) носит название — уравнение непрерывности (уравнение неразрывности). Оно входит в систему уравнений Максвелла в неявном виде. Уравнение непрерывности выражает закон сохранения заряда. Согласно уравнению (6) в точках, которые являются источниками вектора плотности тока ($overrightarrow$), происходит убывание заряда.

Видео:Лекция 2. Уравнение неразрывностиСкачать

Уравнение неразрывности для стационарных токов

В том случае, если токи не зависят от времени, то уравнение (1) переходит в следующее выражение:

А уравнение (6) в равенство:

Уравнение (8) показывает, что если ток является постоянным, то $overrightarrow$ не имеет источников. Это значит, что лини тока нигде не начинаются и нигде не заканчиваются. Можно сделать вывод о том, что линии постоянного тока всегда замкнуты. Под линиями токов в данном случае следует понимать лини вектора $overrightarrow.$ (касательные к которым совпадают с направлением вектора плотности тока в точке касания). Что напрямую следует из (7).

Готовые работы на аналогичную тему

Благодаря замкнутости постоянных токов их можно разложить на совокупность бесконечных замкнутых тонких нитей тока.

Задание: Из уравнения$ rotoverrightarrow=fracoverrightarrow+fracfrac<partial overrightarrow>$, которое принадлежит системе уравнений Максвелла (СГС), получите уравнения непрерывности токов и закон сохранения заряда.

где $overrightarrow$ — напряженность магнитного поля, $c- $скорость света в вакууме,$ overrightarrow$ — вектор электрического смещения.

Проведем для него операцию дивергенции ($div или nabla $). Получим:

[nabla left(rot overrightarrowright)=0left(1.2right).] [ nabla left(fracoverrightarrow+fracfrac<partial overrightarrow>right)=fracleft(4pi nabla overrightarrow+fracnabla overrightarrowright)(1.3).]

[nabla overrightarrow=4pi rho left(1.4right).]

Подставим (1.4) в (1.3) получим:

[fracleft(4pi nabla overrightarrow+frac4pi rho right)=0left(1.5right).]

от сюда следует:

или в интегральной форме:

Соответственно для замкнутых изолированных областей получим:

[ointnolimits_S=0 (1.8)] [intnolimits_V=const (1.9)]

Это уравнение непрерывности для тока, содержащее в себе закон сохранения заряда — один из фундаментальных принципов, который подтверждается экспериментом.

Задание: Объясните, как ведет себя нормальная составляющая вектора плотности тока при переходе через границу двух проводящих сред, для стационарных токов. Что можно сказать относительно нормальной составляющей плотности тока для проводника, который находится в непроводящей среде?

На поверхности соприкосновения двух проводников может испытывать разрыв непрерывности. Но, его нормальная составляющая ($j_n$) должна быть одинаковой по обе стороны границы сред. В противном случае количество электричества, которое притекает к одной стороне не равно, количеству электричества, которое вытекает с другой стороны. Значит:

где $j_-$нормальная составляющая плотность тока в среде (1), $j_-$нормальная составляющая плотность тока в среде (2).

В непроводящей среде $overrightarrow=0$. Следовательно, нормальная составляющая к поверхности проводника плотности тока также должна быть равна нулю:

🎦 Видео

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Что Такое Плотность Электрического Тока. Простыми Словами. Формула Плотности Электрического ТокаСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

60. Уравнения МаксвеллаСкачать

Лекция №6 "Электрический ток"Скачать

Электричество и магнетизм - Лекция 10Скачать

Вывод уравнения неразрывности - Лекция 1Скачать

Уравнения Максвелла Лекция 10-1Скачать

Gos Ekzam 12 13 2 816 kbpsСкачать

Лекция №10. Электростатика и магнитостатикаСкачать

Останина М.В. - Электродинамика.Лекции.Ч.1 - 2. Уравнения Максвелла и их физическое обоснованиеСкачать

75. Уравнения линейной акустикиСкачать

50. Правила КирхгофаСкачать

Теория поля 6. Вторая пара уравнений Максвелла. Законы сохранения ЭМ поля.Скачать

2.3 Закон Гаусса, закон неразрывности магнитных силовых линий. Закон сохранения зарядаСкачать

Соколов В.А. - Электродинамика.Часть 2.Лекции - 9. Постановка задачи для стационарных токовСкачать