Содержательная линия уравнений и неравенств

Видео:Как решают уравнения в России и СШАСкачать

Основные этапы изучения содержательной линии «уравнения и неравенства» в основной школе

Просмотр содержимого документа
«Основные этапы изучения содержательной линии «уравнения и неравенства» в основной школе»

ОСНОВНЫЕ ЭТАПЫ ИЗУЧЕНИЯ СОДЕРЖАТЕЛЬНОЙ ЛИНИИ «УРАВНЕНИЯ И НЕРАВЕНСТВА» В ОСНОВНОЙ ШКОЛЕ

Пропедевтический этап (4– 6 классы)

4 класс. Формирование представления о понятии «уравнение» (с использованием термина). Решение простых уравнений, в которых буквой обозначено неизвестное слагаемое (уменьшаемое, вычитаемое, множитель, делимое, делитель).

5 класс. Изучение понятий уравнения, корня уравнений, что значит решить уравнение. Решение наряду с простыми уравнениями, более сложных, содержащих неизвестное в одной части уравнения.

6 класс. Решение уравнений, содержащих переменную в обеих частях уравнения. Для этого изучается правило переноса слагаемых из одной части уравнения в другую. Применение уравнений к решению текстовых задач.

Систематическое изучение алгебраических уравнений и неравенств (7 – 9 классы)

7 класс. Понятие уравнения с одной и двумя переменными. Изучение понятия и свойств равносильных уравнений. Решение линейных уравнений, систем двух линейных уравнений с двумя переменными, применение уравнений и систем уравнений первой степени к решению текстовых задач.

8 класс. Понятие квадратного уравнения, его решение, формулы для нахождение корней уравнения и теорема Виета. Методы решения уравнений: разложение на множители, метод введения новой переменной. Определение понятий «больше», «меньше», числовые неравенства и их свойства, неравенства с одной переменной и их решение.

9 класс. Понятие дробно-рационального уравнения, его решение и применение к решению текстовых задач. Методы решения уравнений: разложение на множители, метод введения новой переменной.

Видео:Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

Методические аспекты изучения неравенств в основной школе

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Методические аспекты изучения неравенств в основной школе

Аннотация. В статье рассмотрены методические аспекты изучения неравенств в основной школе.

Ключевые слова: неравенство.

Постановка проблемы. Тема «Неравенства» – это составляющая содержательно-методической линии «Уравнения и неравенства». Поэтому очень важно правильно выстроить методику ее изучения без разрыва с другими сопряженными темами.

Неравенства – это одна из самых основных тем школьного курса математики. Она имеет большое внутрипредметное и межпредметное значение. В первом случае неравенства широко используются при изучении тем «Функции» и «Тождественные преобразования», во втором случае показывается их роль и применение в физике и химии.

Основная задача темы «Неравенства» – освоить способы решения различных видов неравенств.

Целью статьи является методически обосновать особенности изучения неравенств в основной школе.

Изложение основного материала. Рациональным шагом, по моему мнению, будет выделение двух основных путей развертывания содержания линии неравенств.

1) Неравенства не могут изучаться без уравнений. Поэтому важно сначала пройти материал, который относится к уравнениям, а потом уже на этой основе можно вводить неравенства.

Если же говорить о возможности раздельного изложения теории неравенств, то его можно проводить исключительно до теории квадратного трехчлена (включительно). Но в дальнейшем раздельное изучение в старших классах не имеет смысла, поскольку логарифмические, показательные, тригонометрические уравнения и соответствующие неравенства изучаются в более тесной связи друг с другом.

2) Основные классы неравенств изучаются сразу вслед за изучением соответствующих классов уравнений.

Отсюда можно сделать вывод, что на протяжении всего изучения неравенств в школе, есть те промежуточные пути, когда некоторые классы уравнений и неравенств сближены друг с другом по времени изучения, а другие, наоборот, не связаны.

Начиная с 1985 по 1990 года тема «Неравенства» начиналась с 4-ого класса. Дальше, после принятия новой программы по математике, теория о неравенствах появилась лишь с 8-го класса.

Проанализировав тематическое планирование темы «Неравенства», то можно сделать вывод о том, что в программе по учебнику Макарычев Ю.Н. Миндюк Н.Г. и др. отводится наибольшее количество часов на изучение темы «Неравенства и системы неравенств». И особое внимание этой теме уделяется в 11 классе (23 часа). Тогда как в программе по учебнику Алимова Ш.А. в 11 классе только 5 часов.

Подытоживая выше сказанное, я считаю, что для получения наилучшего результата по теме «Неравенства и системы неравенств» необходимо использовать учебник Макарычева Ю.Н., Миндюк Н.Г.

Еще полно раскрывает тему учебник Мордкович А. Г., но все же количество часов по программе меньше, чем в учебниках Макарычева Ю.Н., Миндюк Н.Г.

Последовательность изучения различных классов неравенств и систем различна в разных учебниках. Однако количество возможных вариантов для последовательности их введения не слишком велико – классы находятся в определенной логической зависимости друг от друга, которая предписывает порядок их появления в курсе.

Наличие такого разнообразия подходов затрудняет методическое описание, поскольку принятие того или иного пути требует различных приемов изучения материала.

В целом, можно сказать, что изучение неравенств в школьном курсе математики организовано так же, как и уравнений. Все же надо указать некоторые аспекты изучения неравенств.

а) Мне хотелось бы отметить тот факт, что навыки решения неравенств, за исключением квадратных, формируются на более низком уровне, чем уравнений соответствующих классов. Все это связано с рядом объективных причин, а главная из них – теория неравенств намного сложнее теории уравнений.

Указанная проблема при изучении неравенств немного смягчается другими особенностями изучения неравенств. Отсюда можно сделать вывод о том, что в целом содержательная сторона темы «Неравенства», возможности ее приложений от этого не страдают.

б) Практически все приемы решения неравенств основываются на переходе от данного неравенства к соответствующему ему уравнению , которое решив, находим корни, а их базе ищем множество решений исходного неравенства. Такой поход не используется только в случае рассмотрения линейных неравенств, где в нем нет необходимости из-за простоты процесса решения таких неравенств.

Эту особенность необходимо постоянно подчеркивать, с тем, чтобы переход к уравнениям и обратный переход превратились в основной метод решения неравенств; в старших классах он формализуется в виде «метода интервалов».

3) В процессе изучения неравенств главную роль играют наглядно-графические средства.

Все эти, указанные мной, методические аспекты могут быть использованы при:

— обосновании расположения учебного материала по исследуемой теме;

— определении количества заданий, которые нужны для полноценного усвоения программного минимума.

Для иллюстрации сказанного мной выше, приведу несколько примеров. Для начала рассмотрим первый аспект изучения темы «Неравенства». Здесь стоит отметить тот факт, что при одинаковом количестве упражнений, техника решения неравенств какого-либо класса будет ниже, чем уравнений соответствующего класса. Поэтому видим то, что для полноценного формирования прочных знаний, умений и навыков решения неравенств необходимо больше заданий.

Второй аспект состоит в том, что те темы, которые относятся к неравенствам, должны располагаться тем, относящихся к соответствующим классам уравнений.

Третий аспект изучения неравенств показывает зависимость от качества изучения функциональной линии школьного курса.

Подытоживая все методические аспекты изучения неравенств, указанные мной, можно говорить обязательном предшествующем изучении материала по равенствам, поскольку это напрямую влияет на качество изучения темы «Неравенства».

Все аспекты можно показать, например, при изучении материала по теме урока «Квадратные неравенства». Эта тема обязательно должна следовать после проведения урока на тему «Квадратные уравнения» или «Квадратный трехчлен».

До изучения квадратных неравенств дети должны уже уметь:

— строить график квадратичной функции;

— находить нули функции или показать, что их нет.

Прием перехода к квадратным неравенствам можно осуществить путем перехода от неравенства к построению и изучению графика функции .

Хорошо известно, что есть разные случаи расположения графика относительно оси абсцисс. Исходя из этого, рационально будет начать рассмотрение конкретного задания, которое предусматривает рассмотрение соответствующего квадратного трехчлена (с различными корнями).

В результате мы получаем некое соответствие между двумя задачами:

— «Найти решение неравенства »;

— «Найти все аргументы, при которых значение функции положительное».

На основе установленной таким образом связи, происходит переход к построению графика функции. Нули данной функции разбивают ось абсцисс на три промежутка, в каждом из которых она сохраняет знак, поэтому ответ считывается прямо с чертежа.

Аналогию можно провести и для решения остальных случаев решения квадратных неравенств (у квадратного трехчлена не больше одного корня).

Очень часто в курсе математики основной школы многие учителя ограничиваются исключительно изучением неравенств основных классов. То есть по факту они обходят стороной те задания, которые требуют сведения к основным классам. Примером могут послужить биквадратные неравенства.

Также стоит отметить те типы заданий, в которых проявляется прикладная роль неравенств в курсе алгебры:

— нахождение области определения функции;

— исследование корней уравнений в зависимости от параметров.

Основываясь на этом, можно сказать, что ознакомление учащихся с неравенствами позволяет применять на практике аппарат неравенств для решения самых разнообразных задач.

При решении линейных неравенств важно начинать из самого простого до полного его усвоения. То есть дети должны иметь отработанные навыки по решению простейших неравенств вида и при различных значениях а и b. Также важно и понимание учеников того, что решением линейного неравенства является не какое-либо число или несколько чисел, а бесконечное множество чисел – числовой промежуток. Проще говоря, дети должны без проблем решать, например, такие неравенства:

С точки зрения применения в курсе анализа нет необходимости отрабатывать у всех учащихся умения решать неравенства, которые требуют сложных преобразований, и тем самым осложнят процесс усвоения темы. Но, тем не менее, дети должны без особых затруднений уметь решать линейные неравенства вида:

Во время работы с линейными неравенствами с одной переменой важно не забывать о таких свойствах неравенств:

1) если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;

2) если обе части неравенства умножить или разделить на одно и то же отрицательное число, то необходимо изменить при этом знак неравенства на противоположный. В результате получим равносильное ему неравенство.

По моему мнению, следующий алгоритм решения линейных неравенств с одной переменной аналитическим методом, в развернутом виде может быть представлен так:

1) преобразование обеих частей неравенства;

2) приведение подобных членов;

3) приведение неравенства к простейшему виду на основании свойств неравенств;

4) запись ответа.

Проиллюстрируем данный алгоритм на примере: «Решить неравенство: »

Дальше неравенства встречаются в курсе алгебры 9-го класса в теме «Неравенства с одной переменной» при изучении первой главы учебника «Квадратичная функция». Здесь они знакомятся с решением неравенств второй степени с одной переменной и неравенств вида:

где – не равные друг другу числа.

При решении неравенств второй степени с одной переменной, то есть неравенств вида:

где x – переменная, a, b и c – некоторые числа, причем можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.

При решении подобных неравенств придерживаются такого алгоритма действий:

1) нахождение дискриминанта квадратного трехчлена для определения наличия или отсутствия корней;

2) в случае, когда корни есть, необходимо их отметить на оси x. На основе построенных точек, схематически строят параболу, направление ветвей которой зависит от знака коэффициента при старшем члене: вверх при или вниз при . В случае, когда не имеет корней, то схематически изображают параболу, которая располагается в верхней полуплоскости при или в нижней при ;

3) нахождение на оси x промежутков, для которых точки параболы расположены выше оси x (если решают неравенство ) или ниже оси x (если решают неравенство ).

Проиллюстрируем данный алгоритм на примере: «Решить неравенство: »

а) Рассматриваем функцию . Ее график – парабола с направленными вверх ветвями.

б) Расположение параболы относительно оси x. Для этого нужно решить соответствующее уравнение:

Нарисуем, все полученное координатной плоскости (рис. 1).

На основе рисунка делаем вывод, что функция принимает отрицательные значения, когда .

Ответ: множеством решений неравенства есть числовой промежуток .

В данном задании вершина параболы не представляла никакой ценности для решения примера, важным было только направление ветвей и точки пересечения с осью x.

Дальше в обязательном порядке необходимо детей ознакомить с другим способом решения неравенств, так называемым методом интервалов, в частности, неравенства вида (1) решают этим методом.

Полезно после приведения нескольких примеров дать учащимся под запись алгоритм решения неравенств методом интервалов:

1) вводим функцию;

2) находим область определения функции;

3) находим нули функции;

4) разбиваем область определения точками, в которых функция обращается в нуль, на интервалы;

5) определяем знак функции в каждом из этих интервалов;

6) выбираем те интервалы, которые удовлетворяют данному неравенству;

7) записываем ответ.

Проиллюстрируем данный алгоритм на примере: «Решить неравенство: »

Выводы. Умение решать линейные неравенства с одной переменной и квадратные неравенства дает возможность находить решение: логарифмических уравнений и неравенств, тригонометрических неравенств.

Также само на математический аппарат неравенств опирается изучение приближенных вычислений, введение важнейших понятий математического анализа – производной и интеграла.

Кроме того, линия неравенств находится среди тех вопросов, которые получают в курсе алгебры и начал анализа наибольшее развитие. Поэтому определенные умения, связанные с неравенствами, должны быть доведены до автоматизма, должны быть прочно усвоены и отработаны, чтобы на них можно было опираться для развития последующих представлений и умений.

Список использованной литературы

1. Федеральный государственный образовательный стандарт общего основного образования / М-во образования и науки Рос. Федерации. – М.: Просвещение, 2011. – 48 с.

2. Асмолов А.Г. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя/под ред. А.Г. Асмолова. — М.: Просвещение, 2015. – 159 с.

Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Методика изучения неравенств

Федеральное агентство по образованию

Саратовский Государственный Университет им.Н.Г. Чернышевского

Кафедра математики и методов её преподавания

на тему: Методика изучения неравенств

Выполнила: студентка 4 курса 421 группы ММФ

Проверил: зав. каф. к. п. н. Кондаурова И.К.

Видео:Решение неравенства методом интерваловСкачать

Содержание

1. Методика изучения темы «Неравенства» в начальной школе. 5

2. Методика изучения неравенств в старших классах. 11

2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики. 11

2.2 Классификация преобразований неравенств и их систем.. 13

2.3 Общая последовательность изучения материала линии неравенств. 15

3. Методика изучения основных классов неравенств и их систем.. 19

Список использованных источников. 27

Видео:Решение системы неравенств с двумя переменными. 9 класс.Скачать

Введение

Тема «Неравенства» занимает важное место в курсе алгебры. Она богата по содержанию, по способам и приемам решения неравенств, по возможностям ее применения при изучении ряда других тем школьного курса алгебры. Это объясняется тем, что уравнения и неравенства широко используются в различных разделах математики, в решении важных прикладных задач.

Анализ диссертационных работ, посвященных методике изучения темы «Неравенства» в основной школе, показал, что в настоящий момент имеется ряд исследований, раскрывающих ее различные аспекты. Одним из первых было диссертационное исследование К.И. Нешкова, в котором сформулированы принципы отбора содержания и выделен необходимый объем материала по теме. При этом большая роль отводилась упражнениям.

Исследования: М.В. Паюл, И.М. Степуро посвящены вопросам взаимосвязи понятий неравенства, уравнения и функции; М.П. Комова, Г.Н. Солтан — доказательствам и решению неравенств на геометрическом материале; Е.Ф. Недошивкина — внутрипредметным связям при изучении уравнений и неравенств в курсе математики 4-8-х классов; Н.Б. Мельниковой, Д.Д. Рыбдаловой — прикладным аспектам изучения неравенств в средней школе.

Итак, можно констатировать тот факт, что отдельные вопросы методики обучения понятию неравенства и решению конкретных неравенств в школьном курсе математики освещены достаточно полно.

Несмотря на значительный положительный опыт в методике преподавания темы «Неравенства», как показывает анализ результатов тестов, контрольных, выпускных, вступительных экзаменационных работ, учащиеся средней школы недостаточно полно владеют основными знаниями и умениями по решению неравенств. В качестве аргумента приведем анализ результатов участия России в международных исследованиях TIMSS (6-ое место из 36 стран участников), который показал, что наибольшую озабоченность по курсу алгебры вызывает качество знаний и умений учащихся по теме «Неравенства».

Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

1. Методика изучения темы «Неравенства» в начальной школе.

Работа над неравенствами ведется с I класса, органически сочетаясь с изучением арифметического материала. Программа по математике для I-III классов ставит задачу выполнять сравнение чисел, а также сравнение выражений с целью установления отношений «больше», «меньше», «равно»; научить записывать результаты сравнения с помощью знаков и читать полученные неравенства.

Числовые неравенства учащиеся получают в результате сравнения заданных чисел или арифметических выражений. Поэтому знаками соединяются не любые два числа, не любые два выражения, а лишь те, между которыми существуют указанные отношения. Если одно число больше (меньше) другого или одно выражение имеет значение больше (меньше), чем другое выражение, то, соединенные соответствующим знаком, они образуют неравенство. Таким образом, первоначально у младших школьников формируются понятия только о верных неравенствах.

Однако в процессе работы над уравнениями, выражениями и неравенствами с переменной учащиеся, подставляя различные значения переменной, накапливают наблюдения и убеждаются в том, что равенства и неравенства бывают как верные, так и неверные. Такой подход к раскрытию понятий определяет соответствующую методику работы над равенствами, неравенствами, уравнениями.

Ознакомление с неравенствами в начальных классах непосредственно связывается с изучением нумерации и арифметических действий.

Сравнение осуществляется сначала на основе сравнения множеств, которое выполняется, как известно, с помощью установления взаимно однозначного соответствия. Этому способу сравнения множеств учат детей в подготовительный период и в начале изучения нумерации чисел первого десятка. Попутно выполняется счет элементов множеств и сравнение полученных чисел (кружков 7, треугольников 5, кружков больше, чем треугольников, 7 больше, чем 5). В дальнейшем при сравнении чисел учащиеся опираются на их место в натуральном ряду: 9 меньше, чем 10, потому что при счете число 9 называют перед числом 10; 5 больше, чем 4, потому что при счете число 5 называют после числа 4.

Установленные отношения записываются с помощью знаков , учащиеся упражняются в чтении и записи неравенств.

Впоследствии при изучении нумерации чисел в пределах 100, 1000, а также нумерации многозначных чисел сравнение чисел осуществляется либо на основе сопоставления их по месту в натуральном ряду, либо на основе разложения чисел по десятичному составу и сравнения соответствующих разрядных чисел, начиная с высшего разряда (75>48, так как 7 десятков больше, чем 4 десятка; 75>73, так как десятков поровну, а единиц в первом числе больше, чем во втором).

Сравнение величин сначала выполняется с опорой на сравнение самих предметов по данному свойству, а потом осуществляется на основе сравнения числовых значений величин, для чего заданные величины выражаются в одинаковых единицах измерения. Сравнение величин вызывает трудности у учащихся, поэтому, чтобы научить этой операции, надо систематически в I-III классах предлагать разнообразные упражнения, например:

Подберите равную величину: 7 км 500 м = □ м, 3080 кг= □ т □ кг.

Подберите числовые значения величин так, чтобы запись верной: □ ч 16.

Подобные упражнения помогают детям усвоить не только понятия равных и неравных величин, но и отношения единиц измерения.

Переход к сравнению выражений осуществляется постепенно. Сначала в процессе изучения сложения и вычитания в пределах 10 дети длительное время упражняются в сравнении выражения и числа (числа и выражения). Первые неравенства вида 3+1>3, 3-1 3), значит, можно записать: 3+1>3 (три плюс один больше, чем три). Аналогичная работа ведется над неравенством 3-1 5 2 5 2 b, то b 3), а других меньше (3 5, х-4>12, 72: х 0, 6+4> □, 7+ □ 0 можно подставить число 1 (1>□), можно 2 (2>□), можно З (3>□) и т.д. После того как названо несколько чисел, полезно обобщить наблюдения (например, во втором неравенстве можно подставить любое число, которое меньше 10-от 0 до 9).

Рассматривая во II классе, например, неравенство х+3 b к неравенству f(a) >f(b), где f-возрастающая функция, или обратный переход.

3б) Переход от неравенства а 0, помещенная на рис.3. В результате определенной тренировки учащиеся привыкают пользоваться такой схемой, а затем ее мысленным образом.

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

3. Методика изучения основных классов неравенств и их систем

Эти классы можно разбить на две группы. Первая группа рациональные неравенства и системы. Наиболее важными классами соответствующие классы неравенств. Вторая группа — иррациональные и трансцендентные неравенства и системы. В состав этой группы входят иррациональные, показательные, логарифмические и тригонометрические неравенства.

Первая группа получает достаточное развертывание, вплоть до формирования прочных навыков решения, уже в курсе алгебры неполной средней школы. Вторая же группа в этом курсе только начинает изучаться, причем рассматриваются далеко не все классы, а окончательное изучение происходит в курсе алгебры и начал анализа. При изучении второй группы приходится опираться на общие понятия и методы, относящиеся к линии неравенств. Указанное различие, однако, не является единственным, которое противопоставляет эти две группы. Более существенным является учет особенностей, связанных с развертыванием материала каждой из этих групп. По сравнению с первой группой неравенства, входящие в состав второй, в процессе их изучения обнаруживают значительно более сложные связи с другими линиями курса математики — числовой, функциональной, тождественных преобразований и др.

Последовательность изучения различных классов неравенств и систем различна в разных учебниках. Однако количество возможных вариантов для последовательности их введения не слишком велико — классы находятся в определенной логической зависимости друг от друга, которая предписывает порядок их появления в курсе.

Наличие такого разнообразия подходов затрудняет методическое описание, поскольку принятие того или иного пути требует различных приемов изучения материала.

Отметим ряд особенностей в изучении неравенств:

1) Как правило, навыки решения неравенств, за исключением квадратных, формируются на более низком уровне, чем уравнений соответствующих классов. Эта особенность имеет объективную природу: теория неравенств сложнее теории уравнений. Отмеченное обстоятельство отчасти смягчается другими особенностями изучения неравенств, поэтому в целом можно считать, что содержательная сторона неравенств, возможности их приложений от этого не страдают.

2) Большинство приемов решения неравенств состоит в переходе от данного неравенства a>b к уравнению а=b и последующем переходе от найденных корней уравнения к множеству решений исходного неравенства. Пожалуй, такого перехода не производится лишь при рассмотрении линейных неравенств, где в нем нет необходимости из-за простоты процесса решения таких неравенств. Эту особенность необходимо постоянно подчеркивать, с тем? чтобы переход к уравнениям и обратный переход превратились в основной метод решения неравенств; в старших классах он формализуется в виде «метода интервалов».

3) В изучении неравенств большую роль играют наглядно-графические средства.

Указанные особенности могут быть использованы для обоснования расположения материала, относящегося к неравенствам, количества заданий, необходимых для усвоения программного минимума.

Приведем примеры. Первая особенность может быть истолкована так: при выполнении одного и того же числа упражнений техника решения неравенств какого-либо класcа будет ниже, чем уравнений соответствующего класса; следовательно, если имеется необходимость формирования прочных навыков решения неравенств, то для этого требуется большее число заданий. Вторая особенность объясняет то, что темы, относящиеся к неравенствам, расположены после тем, относящихся к соответствующим классам уравнений. В соответствии с третьей особенностью изучение неравенств зависит от качества изучения функциональной линии школьного курса (построение графиков и графическое исследование функций).

Перечисленные особенности показывают, что изучение предшествующего материала сильно влияет на изучение неравенств. Поэтому роль этапа синтеза в изучении неравенств особенно возрастает.

Проиллюстрируем указанные особенности на материале квадратных неравенств. Изучение этого раздела курса следует за изучением квадратного уравнения и квадратного трехчлена. К моменту его изучения учащиеся умеют строить графики квадратичной функции, причем на них отмечаются нули функции, если они существуют. Поэтому переход к рассмотрению квадратных неравенств можно осуществить как переход от неравенства ах²+bх+с>0 к построению и изучению графика функции у=ах²+bх+с. Поскольку возможны различные случаи расположения графика относительно оси абсцисс, лучше начать с рассмотрения конкретного задания, для которого соответствующий квадратный трехчлен имеет различные корни. На этом примере устанавливается соответствие между двумя задачами: «Решить неравенство ах²+bх+с>0»; «Найти значения аргумента, для которых значения функции у=ах²+bх+с положительны». Посредством этой связи производится переход к построению графика функции. Нули этой функции разбивают ось абсцисс на три промежутка, в каждом из которых она сохраняет знак, поэтому ответ считывается прямо с чертежа. Другие случаи решения квадратных неравенств (у квадратного трехчлена ах²+bх+с не больше одного корня) требуют дополнительного рассмотрения, но опираются на то же соответствие.

В процессе дальнейшего изучения устанавливается, что нет нужды в точно вычерченном графике квадратного трехчлена, достаточно наметить только положение корней, если они есть, и учесть на эскизе нужные особенности графика (направление ветвей параболы).

В школьном курсе математики ограничиваются изучением только неравенств основных классов; задания, которые требуют сведения к основным классам, встречаются сравнительно редко. Например, не изучаются биквадратные неравенства.

Из числа типов заданий, в которых проявляется прикладная роль неравенств в курсе алгебры, отметим нахождение области определения функции и исследование корней уравнений в зависимости от параметров.

Иррациональные и трансцендентные неравенства

Определения различных классов иррациональных и трансцендентных неравенств, которые приводятся в школьных учебниках, обычно имеют вид: «Неравенство называется иррациональным (показательным в т.д.), если оно содержит неизвестное под знаком корня (в показателе степени и т.д.)». Несмотря на формальную расплывчатость, определения такого типа достаточны для того, чтобы указать некоторую область, уравнения или неравенства из которой решаются способами, изучаемыми при прохождении соответствующей темы. В каждом из таких классов можно указать подклассы простейших уравнений или неравенств, к которым и сводится решение более сложных заданий.

Каждый простейший класс тесно связан с классом соответствующих функций; по существу, формулы решений и исследование простейших неравенств здесь опираются на свойства функций. В начале изучения каждого простейшего класса учащимся приходится преодолевать трудности, связанные с освоением специфической символики, в частности узнавать новые формы записи чисел и числовых областей, в которых должен быть получен ответ к заданию. При решении заданий часто используются наряду с известными специфические для соответствующего класса функций тождества. Значительно чаще, чем в предшествующей части курса, в решении неравенств используются неравносильные преобразования, широко используются подстановки. Поэтому весь этот материал требует достаточной логической грамотности учащихся.

Специфика трансцендентных неравенств. При рассмотрении различных классов трансцендентных неравенств необходимо уделять достаточное внимание формированию навыка применения тождеств для преобразования данных неравенств. Особенно ярко это проявляется в тригонометрии, поэтому при изучении тригонометрических неравенств большое значение приобретают задания и системы вопросов, связанные с распознаванием применимости того или иного тождества, возможности приведения уравнения или неравенства к определенному виду.

Здесь значительные трудности связаны с тем, что некоторые тождества, используемые в преобразованиях, приводят к изменению области определения. К числу таких тождеств относятся, например, такие:

Использование этих тождеств слева направо может привести к потере корней, а справа налево — к появлению посторонних корней. Рассмотрим примеры.

Здесь учет ограничений при использовании тождества для логарифма произведения выполнен при втором переходе, в результате чего неравенство преобразовалось в систему неравенств, из которых два последних позволяют сохранить исходную область определения неизменной.

В результате выполнения аналогичных заданий можно сделать вывод: если приходится пользоваться преобразованиями, расширяющими область определения, то для сохранения равносильности необходимо дополнительно ввести ограничения, сохраняющие исходную область определения неизменной.

Видео:Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Заключение

В данной курсовой работе мы рассмотрели методику преподавания темы «Неравенства» в начальных и старших классах средней школы.

Неравенство числовое — высказывание вида а b, где или b, то b а.

К обеим частям истинного (верного) числового неравенства можно прибавлять одно и то же число, в результате получим истинное неравенство. Умножая обе части истинного числового неравенства а bс.

Содержание линии неравенств развертывается на протяжении всего школьного курса математики. Учитывая важность и обширность материала этой линии, еще раз отметим целесообразность на заключительных этапах обучения предлагать достаточно разнообразные и сложные задания, рассчитанные на активизацию наиболее существенных компонентов этой линии, основных понятий и основных приемов решения, исследования и обоснования заданий.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Список использованных источников

1. Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах: Уч. пос. для уч-ся школ. отд-й пед. уч-щ / Под ред. М.А. Бантовой. -3-е изд., испр. — М.: Просвещение, 1984 г. — 335 с. — ил.

2. Бантова М.А. Методическое пособие к учебнику математики/М.А. Бантова, Т.В. Бельтюкова, С.В. Степанова. – М.: Просвещение, 2001 – 64 с.

3. Вавилов В.В., Мельников И.И. и др. «Задачи по математике. Уравнения и неравенства» М.: Изд. «Наука» 1987 г.

4. Давыдов В.В., С.Ф. Горбов и др. Обучение математике. – М.: Мирос, 1994. – 192 с.

5. Истомина Н.Б. Методика обучения математике в начальных классах. – М.: Академия, 2000. – 288 с.

6. Кипнис И.М. Задачи на составление уравнений и неравенств: Пос. для учит-й. — М.: Просвещение, 1980 г. -68 с.

7. Левитас Г.Г. Современный урок математики. Методика преподавания. ПТУ-М.: Высшая школа, 1989. -88 с. — ил.

8. Методика преподавания математики в средней школе: Общая методика: Уч. пос. для студ. пед. инст-в по спец.2104 «Математика» и 2105 «Физика»/ А. Блох, Е.С. Канин и др. Сост.Е.С. Черкасов, А.А. Столяр. — М.: Просвещение, 1985. -336 с.

9. Методика преподавания математики в средней школе: Частная методика: Уч. пос. для студ. пед. инст-в по физ-мат. спец-м/ А. Блох, В.А. Гусев, Г.В. Дорофеев и др. Сост.В.И. Мишин. — М.: Просвещение, 1987. -416 с.: ил.

10. Методика преподавания математики в средней школе. /В.А. Ованесян и др. – М: Просвещение, 1980. – 368 с.

11. Олехник С.Н., Потапов М.К., Пасиченко П.И. Нестандартные методы решения уравнений и неравенств. — М.: МГУ, 1991 г.

💥 Видео

Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Неравенства с двумя переменными. 9 класс.Скачать

A.1.3 Линейные уравнения, неравенства и системы неравенствСкачать

Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Это просто! Как решать Показательные Неравенства?Скачать

Решение системы линейных неравенств с одной переменной. 6 класс.Скачать

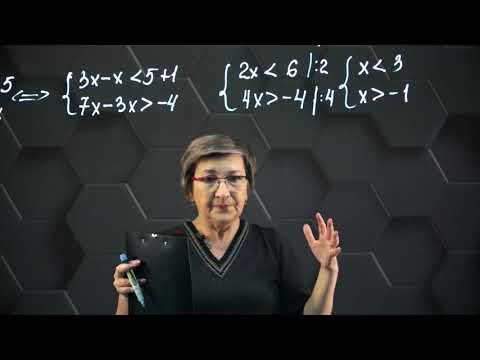
Алгебра 10 класс (Урок№19 - Равносильные уравнения и неравенства.)Скачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать