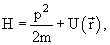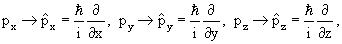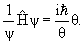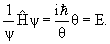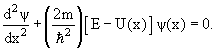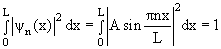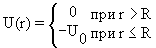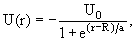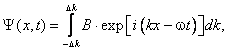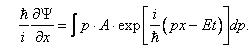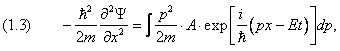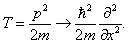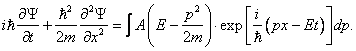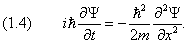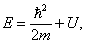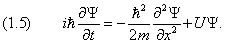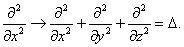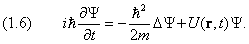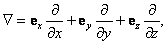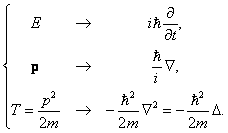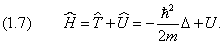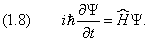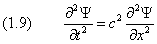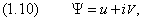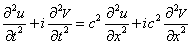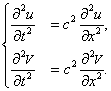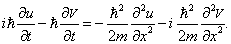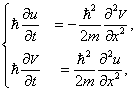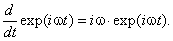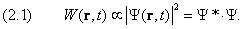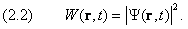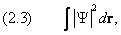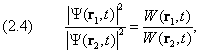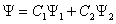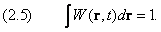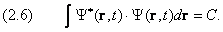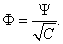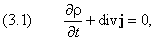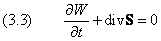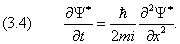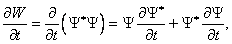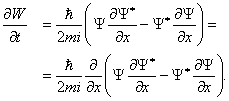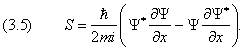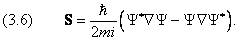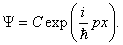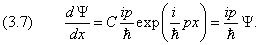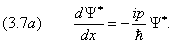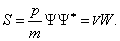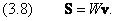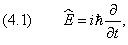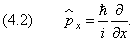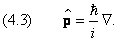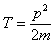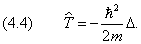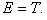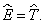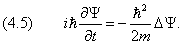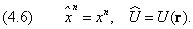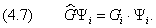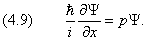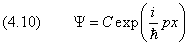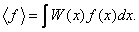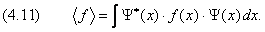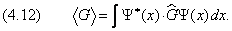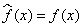9.4.Уравнение Шредингера для стационарных состояний
В развитие идеи де Бройля о волновых свойствах частиц Шредингер в 1926 г. получил уравнение

где m — масса частицы, 
Решение уравнения Шредингера позволяет найти волновую функцию Y (x, y, z, t) частицы, которая описывает микросостояние частицы и ее волновые свойства.
Если поле внешних сил постоянно во времени (т.е. стационарно), то U не зависит явно от t. В этом случае решение уравнения (20) распадается на два множителя
Y (x, y, z, t) = y (x, y, z) exp[-i(E/
где E/
В стационарном случае уравнение Шредингера имеет вид

где Е, U — полная и потенциальная энергия, m — масса частицы.
Следует заметить, что исторически название «волновой функции» возникло в связи с тем, что уравнение (20) или (22), определяющее эту функцию, относится к виду волновых уравнений.
9.5. Собственные функции и собственные значения. Свободная частица
Функции Y , удовлетворяющие уравнению Шредингера при данных U, называются собственными функциями.
Значения Е, при которых существуют решения уравнения (22), называются собственными значениями.
В качестве примера определим y и Е для свободной частицы.
Свободной называют частицу, на которую не действуют силы, т.е. 



Прямой подстановкой можно убедится, что частным решением этого уравнения является функция y (х)=Аexp(ikx), где А=сonst, k=const c собственным значением энергии
Е= 
C учетом (21) волновая функция
Y (х)=Аexp(-i w t+ ikx)= Аexp[-(i/
здесь w =Е/
Функция (25) представляет собой плоскую монохроматическую волну де Бройля [cм. (16)].
Из (24) следует, что зависимость энергии от импульса
Е= 
оказывается обычной для нерелятивиских частиц. Следовательно, энергия свободной частицы может принимать любые значения, т.е. ее энергетический спектр является непрерывным.
Плотность вероятности обнаружить частицу в данной точке пространства
т.е. все положения свободной частицы в пространстве являются равновероятными.
- Собственных значений энергии для уравнения шредингера
- 4.1. Уравнение Шредингера
- Уравнение Шредингера
- 4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
- 4.3. Гармонический осциллятор
- Частица в одномерной потенциальной яме
- 4.4. Частица в поле с центральной симметрией
- 4.5. Орбитальный момент количества движения
- 4.6. Спин
- 4.7. Полный момент количества движения
- 4.8. Квантовые числа
- Таблица квантовых чисел
- Задачи
- Собственных значений энергии для уравнения шредингера
- 8.1. Уравнение Шредингера
- 2.1. Волновая функция
- Волновая функция как вероятность
- Принцип суперпозиции
- Нормировка
- 8.3 Ток вероятности
- 8.4 Операторы физических величин
- Среднее значение.
- 🌟 Видео
Видео:Петров С.В. - Квантовая механика - 7. Особенности решения уравнения ШредингераСкачать

Собственных значений энергии для уравнения шредингера
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
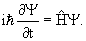 | (4.1) |
где 
в которой 







х → 


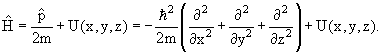 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


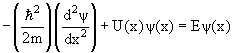
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
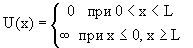 | (4.5) |
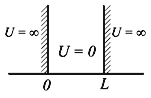
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
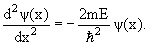 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
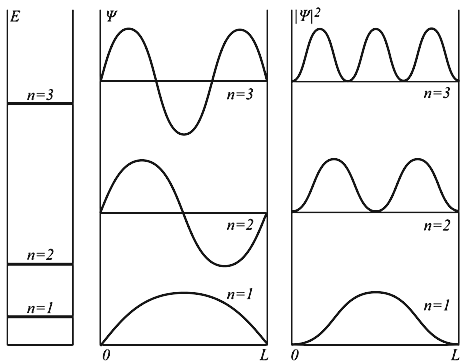
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
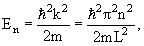 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
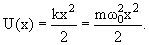 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
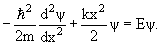 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
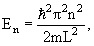

Одномерный гармонический осциллятор:
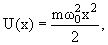
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
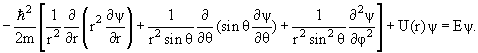 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
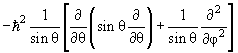 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 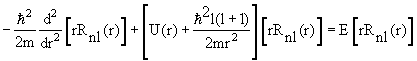 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
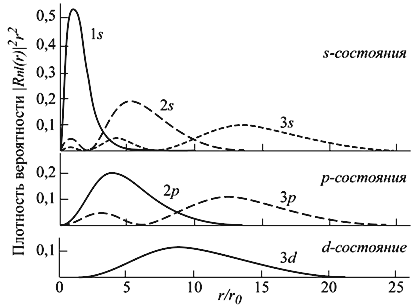
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
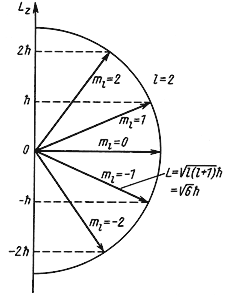
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
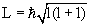 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
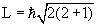
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Видео:Урок 455. Уравнение ШрёдингераСкачать

Собственных значений энергии для уравнения шредингера
Задачи атомной физики решаются методами квантовой теории, которая принципиально отличается от классической механики.
Решение задачи о движении тела макроскопических размеров основано на применении второго закона Ньютона. Если известны силы, действующие на тело, то сначала мы находим его ускорение, затем — траекторию, после чего — все параметры движения. Но в масштабах атомов понятие траектории теряет свой смысл. Своё значение сохраняют так называемые интегралы движения. К ним относятся, в первую очередь, энергия, импульс, момент вращения и чётность. В квантовой теории эти величины определяются сразу, минуя этап вычисления траектории.
В основе расчётов лежит уравнение Шредингера. Решив его, мы находим набор энергетических уровней, который реализуется в заданном потенциале, а также получаем информацию статистического характера о возможном положении частицы.
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

8.1. Уравнение Шредингера
Уравнение Шредингера, как законы Ньютона и уравнения Максвелла, вывести нельзя. Оно основано на анализе экспериментальных данных и в масштабах атомов описывает волновые свойства частиц. Покажем связь уравнения Шредингера с волновым пакетом. Для этого запишем уравнение волнового пакета:
где B — амплитуда. Будем считать, что величина B как функция k равна нулю при k Δ k и k > Δ k . Тогда областью интегрирования становится вся числовая ось. Вспоминая соотношения де Бройля-Эйнштейна (формулы (2.1) и (2.1а) первой главы), приходим к новой записи выражения для волнового пакета
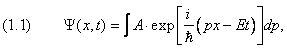
Продифференцируем (1.1) по времени:
Появлению энергии в подынтегральной функции соответствует оператор дифференцирования
Его называют оператором энергии . Импульс, в свою очередь, связан с оператором
в чём можно убедиться, дифференцируя (1.1) по x :
Мы рассматриваем нерелятивистскую частицу в отсутствие внешних полей, следовательно, ее энергия равна p2/2 m. Ей можно сопоставить оператор двойного дифференцирования по координате:
Вычитая (1.3) из (1.2), получим
Всё подынтегральное выражение вместе с разностью 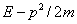
Мы вывели одномерное уравнение Шредингера для свободной частицы. Теперь учтём возможное присутствие внешних полей:
Здесь U = U( x , t ) — потенциальная энергия, зависящая только одной координаты. Вообще говоря, она может также меняться со временем. Соответственно, приходим к одномерному уравнению Шредингера:
Обобщение на случай трёх измерений сводится к замене производной по x оператором Лапласа:
Уравнение Шредингера с потенциалом, зависящим от всех трёх координат, имеет вид
Вектору импульса в трёхмерном случае соответствует оператор градиента:
где e x , e y и e z — единичные векторы в направлении координатных осей. В процессе вывода мы использовали следующие соотношения между физическими величинами и операторами:
Оператор принято отмечать «шляпкой». Например, оператор, отвечающий физической величине G, обозначается как Ĝ. В квантовой механике вводится оператор энергии, или оператор Гамильтона
Он позволяет записать уравнение Шредингера следующим образом:
Уравнение Шредингера содержит мнимую единицу i , следовательно, его решение должно быть комплексным. Этим оно отличается от волнового уравнения в классической механике . В качестве примера рассмотрим одномерный случай. Классическое уравнение
позволяет работать отдельно с действительной и мнимой частями Y , каждая из которых подчиняется одному и тому же уравнению. В самом деле, если
где u и V — действительные функции, то уравнению (1.9), которое мы теперь запишем в виде
равносильна система одинаковых уравнений, каждое из которых совпадает с исходным :
Действительная и мнимая части Y разделились. Мы убедились, что в классическом случае нет принципиальной необходимости в комплексном представлении (хотя оно часто используется для удобства вычислений). Для уравнения Шредингера это не так. Разложение (1.10) вставим теперь в уравнение (1.4):
Этому уравнению эквивалентна система
в которой переменные u и V связаны друг с другом.
Структура уравнения Шредингера
показывает, что оно отображает закон сохранения энергии.
Уравнение Шредингера определяет зависимость волновой функции от времени и от координат. Как второй закон Ньютона описывает траекторию частицы, так уравнение Шредингера описывает эволюцию волновой функции.
Выход в комплексную плоскость является следствием требования, чтобы волновая функция в любой момент времени полностью определялась её начальным значением. Следовательно, уравнение Шредингера должно содержать только первую производную волновой функции по времени, но не вторую. Если ограничиться гармоническими функциями в действительной области, то волновое уравнение обязано содержать вторую производную. В самом деле, однократное дифференцирование переводит синус в косинус и наоборот. Но колебания могут быть описаны экспонентой с комплексным показателем. Её важное свойство заключается в том, что первая производная функции возвращает нас к ней самой:
Перейдём к обсуждению физического смысла волновой функции.
Видео:97. Микрочастица в потенциальной ямеСкачать

2.1. Волновая функция
Выкладки предыдущего раздела мы проводили, используя представление классической механики о волновом пакете. В уравнении Шредингера функция Y ( r , t ) приобретает новый смысл. Она называется волновой функцией и описывает уже не суперпозицию колебаний, но состояние реальной частицы. Перечислим основные свойства волновой функции.
Волновая функция как вероятность
В квантовой механике вся информация о частице содержится в её волновой функции. С учётом соотношения неопределённостей, эта информация носит вероятностный характер. А именно, квадрат модуля волновой функции пропорционален вероятности W найти частицу в данной точке в заданный момент времени:
Здесь звёздочка означает комплексное сопряжение. В большинстве задач, которые нам встретятся в дальнейшем, имеет место точное равенство:
Выбор между (2.1) и (2.2) определяется степенью локализации частицы в пространстве. Если вероятность найти частицу в удалённых точках исчезающе мала, то интеграл
взятый по всему пространству, сходится. В конечном итоге именно это и делает возможным равенство (2.2). Наоборот, свободно движущаяся частица может быть обнаружена в любой точке. Интеграл (2.3) для её волновой функции расходится и, следовательно, | Y | 2 не может служить вероятностью никакой величины. В этом случае справедливо отношение
которое является следствием (2.1). Ниже нам неоднократно будут встречаться волновые функции, модуль которых не стремится к нулю при удалении от начала координат, либо убывает слишком медленно. Хотя для таких функций не имеет смысла (2.2), тем не менее, отношение значений W в двух разных точках пространства равно отношению вероятностей обнаружить там частицу.
Принцип суперпозиции
Уравнение Шредингера линейно относительно волновой функции. Следовательно, любая линейная комбинация
его решений Y 1 и Y 2 также является его решением.
Таким образом, линейная комбинация волновых функций обязательно описывает некоторое состояние частицы (или системы частиц). В частности, при C2 = 0 получаем, что решение уравнения Шредингера, известно с точностью до постоянного множителя.
Нормировка
Вероятность W по своему смыслу должна удовлетворять условию нормировки
Если частица совершает своё движение в ограниченной области, то, согласно предыдущему разделу, существует интеграл:
При выполнении последнего равенства волновая функция может быть преобразована так, чтобы условие
имело место даже в том случае, когда константа C не равна единице. А именно, условию (2.7) удовлетворяет функция
Согласно сказанному в предыдущем разделе, обе эти функции описывают одно и то же состояние. Процесс перехода от Y к F называется нормировкой, а функция F — норми p ованной волновой функцией.
Видео:QM_03 (Операторы импульса и энергии, уравнение Шредингера)Скачать

8.3 Ток вероятности
В газодинамике известно уравнение непрерывности для потока вещества
где r — плотность, а
поток вещества, движущегося со скоростью v . Оно справедливо в том случае, если нет источников и стоков частиц. Аналогичное соотношение
можно вывести и для плотности вероятности W . Сначала проведём расчёты для одномерного случая. Для определения вектора тока вероятности S воспользуемся уравнением Шредингера (1.4) для свободной частицы. Запишем его также для комплексно–сопряжённой волновой функции:
то, подставляя сюда выражения (1.4) и (3.4) для производных по времени от Y и Y *, находим
Последнее уравнение представляет собой аналог одномерного уравнения непрерывности, если поток вероятности принять равным
Обобщение на случай трёх измерений даёт уравнение непрерывности (3.3) с дивергенцией вектора
Физический смысл определённого таким образом потока вероятности S можно выяснить, вычислив его для свободной частицы, то есть, для волновой функции вида
Производная 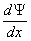
Аналогично вычисляем производную от комплексно сопряжённой функции:
Подставляя (3.7) и (3.7а) в (3.5), получаем
Нетрудно убедиться, что в трёхмерном случае мы приходим к формуле
Она полностью аналогична (3.2), где роль плотности выполняет плотность вероятности W, а вместо потока массы j надо подставить вектор S.
Поток вероятности равен нулю в случае действительной волновой функции. Следовательно, последняя описывает финитное движение, то есть, движение в ограниченной области пространства.
Видео:Уравнение Шрёдингера уравнение на собственныеСкачать

8.4 Операторы физических величин
В этом разделе мы соберём вместе явные выражения для самых важных для нас операторов. Оператор энергии сводится к дифференцированию по времени:
а оператор проекции импульса на одну из координат — к дифференцированию по этой координате:
Аналогичные формулы справедливы для проекций момента на две другие оси, а в трёхмерном случае
вектор импульса выражается через оператор градиента:
При формировании операторов можно пользоваться соотношениями между классическими величинами. Так, оператор кинетической энергии 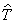
выражается посредством оператора Лапласа:
В отсутствие внешних полей полная энергия частицы равна её кинетической энергии:
В квантовой механике этому факту соответствует уравнение Шредингера для свободной частицы:
Последняя формула является обобщением (1.4) на случай трёх измерений.
Оператор координаты сводится к простому умножению на эту координату. То же самое справедливо и для оператора, представляющего любую функцию координат. Например,
В последующих разделах мы познакомимся с оператором момента вращения.
С математической точки зрения уравнения квантовой механики сводятся к линейной задаче на собственные значения с заданными граничными условиями.
Здесь Y i — собственные функции, а G i — собственные значения оператора 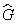
Спектр собственных значений может быть как дискретным, так и непрерывным. Например, непрерывным является спектр импульса свободной частицы. Покажем это для одномерного случая. Вычислим собственное значение p проекции импульса на ось x :
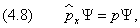
Решение последнего уравнения
в комплексной форме выражает «мгновенную фотографию» плоской монохроматической волны, распространяющейся вдоль оси x . Не удивительно, что мы получили именно такое решение, так как мы исходили из представления плоских волн при получении уравнения Шредингера. Временнýю часть волновой функции мы установим позже.
Отметим важную особенность функции (4.10): квадрат её модуля равен константе |C| 2 . Следовательно, свободно летящая частица с равной вероятностью может находиться в любой точке пространства. Как уже было сказано в разделе (2.1), такую функцию невозможно нормировать приведённым там способом. Таким образом, она представляет собой пример волновой функции, квадрат модуля которой пропорционален вероятности в смысле (2.4), но не имеет места (2.1).
Среднее значение.
В этом разделе мы с самого начала предполагаем, что волновая функция квадратично интегрируема, то есть существует интеграл (2.6). Как известно из математики, среднее значение 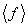
Для операторов, зависящих только от координат, это определение без всяких изменений переносится в квантовую механику. Нужно только вместо вероятности написать квадрат модуля волновой функции:
Здесь интегрирование ведётся по всей области изменения аргумента x .
В общем случае, когда физическая величина G не является функцией координат (например, импульс), её среднее значение определяется как
Подынтегральная функция состоит из двух сомножителей: Y * ( x ) и 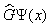
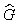
Пусть система находится в определённом состоянии, соответствующем собственному значению G i и собственному вектору — волновой функции Y i . Если физическую величину G усреднять с помощью функции Y i , то среднее значение 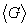
🌟 Видео
Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Квантовая механика 47 - Стационарное уравнение Шредингера. Гармонический осциллятор.Скачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать

96. Уравнение ШредингераСкачать

Уравнение ШрёдингераСкачать

Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать

Петров С.В. - Квантовая механика - 8. Решение стационарного уравнения ШредингераСкачать

Теория Бора. Гипотеза де Бройля. Принцип неопределенности. Уравнение Шрёдингера.Скачать

Лекция №04 "Уравнение Шредингера"Скачать

Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать

Урок 459. Обзор квантовой теории атома водородаСкачать

Классические уравнения | одномерное стационарное уравнение Шрёдингера | беск. потенц. яма | 2Скачать

10. Уравнение ШрёдингераСкачать