Собственные колебания системы описываются уравнением движения x 4x 0 циклическая частота

1. Закон Паскаля можно сформулировать следующим образом.

a. На тело, погруженное в жидкость, действует выталкивающая сила, равная весу

b. Давление в неподвижной несжимаемой жидкости определяется по формуле: P=ρgh

c. Поток жидкости сквозь систему пропорционален разности давлений на её входе и выходе

d. Давление в любом месте покоящейся жидкости одинаково по всем направлениям и передаётся по всему объёму этой жидкости

2. Давление в неподвижной несжимаемой жидкости ….

a. не зависит от расстояния до её поверхности

b. не зависит от рода жидкости

c. зависит от расстояния до её поверхности и не зависит от рода жидкости

d. определяется по формуле: P=P₀+ρgh

3. Закон Архимеда можно сформулировать следующим образом.

a. На тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной жидкости

b. Давление в любом месте покоящейся жидкости одинаково по всем направлениям и одинаково передаётся по всему объёму этой жидкости

c. Давление в неподвижной несжимаемой жидкости определяется по формуле: P=ρgh

d. Поток жидкости сквозь систему пропорционален разности давлений на её входе и выходе

4. Закон Архимеда описывается следующей формулой.

a. движение жидкости

b. совокупность частиц движущейся жидкости

c. линия, касательные к которой в каждой точке направлены вдоль скорости движения частиц жидкости

d. часть жидкости, ограниченная линиями тока

a. линия, касательные к которой в каждой точке направлены вдоль скорости движения частиц жидкости

b. часть жидкости, ограниченная линиями тока

c. совокупность частиц движущейся жидкости

d. движение жидкости

7. Линия тока – это ….

a. область, внутри которой частицы жидкости имеют ненулевую скорость движения

b. совокупность частиц движущейся жидкости

c. совокупность точек, в которых направления скорости движения частиц жидкости и градиента этой скорости совпадают

d. линия, касательные к которой в каждой точке направлены вдоль скорости движения частиц жидкости

8. Трубка тока – это ….

a. часть жидкости, ограниченная линиями тока

b. область, внутри которой частицы жидкости имеют ненулевую скорость движения

c. совокупность частиц движущейся жидкости

d. линия, касательные к которой в каждой точке направлены вдоль скорости движения частиц жидкости

9. Идеальная жидкость – это жидкость ….

a. с нулевой плотностью

b. для которой выполняются законы Паскаля и Архимеда

c. в которой отсутствует внутреннее трение

d. для которой выполняется закон Бернулли

10. Стационарным называют течение ….

a. параметры которого не зависят от координаты

b. для которого выполняются законы Паскаля и Архимеда

c. которое не изменяется со временем

d. для которого число Рейнольдса не превышает 1000

11. Полное давление в потоке ….

a. определяется выражением P_п=ρV 2 /2+ρgh

b. определяется выражением P_п=F/S+ρgh

c. это сумма нормального и тангенциального давлений

d. это сумма гидростатического и динамического давлений

12. Формула Торричелли ….

a. показывает, что скорость истечения жидкости такая же, как скорость, приобретаемая телом при падении с соответствующей высоты

b. позволяет определить давление в потоке несжимаемой жидкости

c. позволяет определить давление в неподвижной несжимаемой жидкости

d. описывает зависимость потока жидкости сквозь систему от разности давлений на её входе и выходе и геометрических параметров системы

13. Работа реактивного двигателя основана на ….

a. законе сохранения энергии

b. использовании давления струи вытекающих газов на окружающие тела

c. возникновении динамического давления в струе газов

d. действии силы реакции вытекающих газов

14. Особенность реактивного двигателя по сравнению с тепловым состоит в том, что ….

a. он более экономичен

b. он позволяет получать большую силу тяги

c. у него больший коэффициент полезного действия

d. он может приводить в движение аппараты, находящиеся в вакууме

15. Вязкость – это ….

a. свойство жидкости оказывать сопротивление перемещению её слоёв друг

b. величина, характеризующая свойство жидкости передавать приложенное к ней

c. обусловленное тепловым движением молекул проникновение одних веществ в

объём, занятый другими веществами

d. свойство жидкости изменять свой объём при изменении давления

16. При ламинарном течении ….

a. слои жидкости перемешиваются между собой

b. параметры потока не изменяются со временем

c. слои жидкости не перемешиваются между собой

d. не выполняется условие непрерывности

17. Число Рейнольдса ….

a. определяет характер течения жидкости

b. определяет величину силы сопротивления движению твёрдого тела в жидкости

c. это отношение динамического давления к статическому в потоке жидкости

d. показывает, выполняется ли условие непрерывности

18. Число Рейнольдса ….

a. пропорционально скорости движения жидкости

b. обратно пропорционально скорости движения жидкости

c. не зависит от скорости движения жидкости

d. обратно пропорционально квадрату скорости движения жидкости

19. Ламинарный режим течения наблюдается при числах Рейнольдса ….

20. Формула Стокса ….

a. определяет характер течения жидкости

b. определяет величину силы сопротивления движению твёрдого тела в жидкости

c. описывает соотношение динамического и статического давления в потоке жидкости

d. показывает, выполняется ли условие непрерывности

21. При движении тела в вязкой жидкости сила сопротивления не зависит от ….

a. вязкости жидкости

c. скорости движения

d. размеров тела

22. Формула Пуазейля ….

a. показывает, что скорость истечения жидкости такая же, как скорость, приобретаемая телом при падении с соответствующей высоты

b. позволяет определить давление в потоке несжимаемой жидкости

c. описывает зависимость потока жидкости от разности давлений и размеров трубы

d. позволяет определить давление в неподвижной несжимаемой жидкости

23. Поток жидкости через трубу ….

a. обратно пропорционален разности давлений на её концах

b. пропорционален квадрату разности давлений на её концах

c. прямо пропорционален разности давлений на её концах

d. пропорционален четвёртой степени разности давлений на её концах

24. При ламинарном течении поток жидкости через трубу круглого сечения при постоянном перепаде давлений на её концах ….

a. пропорционален четвёртой степени радиуса трубы

b. пропорционален квадрату радиуса трубы

c. пропорционален радиусу трубы

d. обратно пропорционален радиусу трубы

25. Уровень жидкости в сосуде 20 см. Скорость вытекания этой жидкости из отверстия в дне сосуда равна …. Жидкость, вытекающая из отверстия в дне наполненного ведра, может иметь максимальную скорость ….

26. Масса батискафа объёмом 5 м 3 не должна быть меньше ….

27. Давление слоя воды в водоёме на глубине 1 м равно ….

28. Высота ртутного столба в манометре составляет 760 мм. Плотность ртути 13600 кг/м 3 . При этом атмосферное давление составляет ….

29. Две трубы длиной 1 м и диаметрами 10 и 5 см включены параллельно друг другу. Объём жидкости, проходящей через трубу меньшего диаметра – 1 л/с. Объём жидкости, проходящей через трубу большего диаметра ….

30. Давление на входе трубы длиной 2 м составляет 16 Па, а на выходе – 4 Па. В средней части трубы давление составляет ….

31. Наливная горловина заполненного жидкостью резервуара имеет диаметр 5 см. В неё поступает жидкость со скоростью 2 см/с. Из сливного отверстия диаметром 10 см этого резервуара одновременно вытекает жидкость со скоростью ….

32. При скорости течения 2 см/с динамическое давление в водопроводной трубе составляет ….

33. Диаметр малого цилиндра гидравлического домкрата – 1,5 см, а большого цилиндра – 3 см. Чтобы с помощью этого домкрата поднять груз массой 1т. к его поршню необходимо приложить силу ….

34. Уровень воды в резервуаре – 5 м. Динамическое давление в открытом сливном отверстии этого резервуара ….

35. Максимальное давление, которое может оказывать вытекающая из отверстия в боковой стенке ведра струя воды, составляет примерно ….

36. После установления стационарного движения камня массой 2 кг, падающего на дно водоёма, сила сопротивления равна ….

37. Величина качества крыла равна двум. Сила сопротивления движению крыла – 100 Н. Подъёмная сила ….

Раздел 11. Колебания

1. Колебание можно определить как ….

a. процесс, имеющий некоторую степень повторяемости во времени

b. процесс возвращения системы в равновесное состояние

c. изменение некоторой величины со временем

d. периодическое изменение некоторой величины в пространстве

2. При совпадении частоты внешней силы и собственной частоты системы, колебания называются ….

3. В том случае если система сама задаёт периодичность воздействия на неё внешней силы, её колебания называются ….

4. При периодическом изменении какого-либо параметра колебательной системы, её колебания называются ….

5. Гармоническими называют колебания ….

a. у которых фаза изменяется со временем по гармоническому закону

b. с постоянным периодом

c. которые описываются гармоническими функциями

d. которые совершаются на резонансной частоте

6. Круговая частота незатухающих собственных упругих колебаний связана с параметрами колебательной системы следующим образом:

7. Фаза колебаний – это ….

a. аргумент периодической функции, описывающей колебания

b. текущий момент времени

c. параметр колебательной системы

d. определённый повторяющийся момент колебаний

8. Фаза колебания ….

a. имеет размерность времени

b. имеет размерность угла

c. не имеет размерности

d. имеет размерность длины

9. При резонансе ….

a. амплитуда вынужденных колебаний достигает максимума

b. фаза вынужденных колебаний достигает максимума

c. начальная фаза колебаний равна нулю

d. внешнее воздействие оказывается в фазе с колебаниями системы

10. Резонансная частота колебаний в системе с трением … собственных колебаний.

a. меньше частоты

b. больше частоты

c. равна частоте

d. может быть больше, меньше или равна частоте

11. Математический маятник – это ….

a. физическое тело, совершающее колебания под действием силы тяжести

b. материальное тело, подвешенное на невесомой упругой нити

c. груз, закреплённый на пружине

d. материальная точка, подвешенная на невесомой нерастяжимой нити

12. Физический маятник – это ….

a. материальная точка, подвешенная на невесомой нерастяжимой нити

b. материальное тело, подвешенное на невесомой упругой нити

c. груз, закреплённый на пружине

d. физическое тело, совершающее колебания под действием силы тяжести

13. Циклическая частота колебаний груза массой 20 г, закреплённого на невесомой пружине с коэффициентом жёсткости 0,32 Н/м равна ….

14. Циклическая частота колебаний математического маятника массой 200 г, подвешенного на нити длиной 16 см ….

15. Циклическая частота колебаний маятника 5 рад·с -1 . Период его колебаний равен ….

16. Колебания точки описываются выражением: x=2sin(5t+2). Начальная фаза колебаний равна ….

17. Колебания точки описываются выражением: x=2sin(5t+2). Через 2 с после начала колебаний их фаза равна ….

18. Решением уравнения x¢¢+4 x = 0 является функция ….

19. Собственные колебания системы описываются уравнением движения: x¢¢+3x¢+4x=0. Под действием внешней силы: f(t)=5sin(t/2π) эта система будет колебаться с частотой ….

20. Собственные колебания системы описываются уравнением движения x¢¢+4 x =0. Циклическая частота колебаний этой системы равна ….

21. Собственные колебания системы описываются уравнением движения: x¢¢+2x¢+64x=0. Коэффициент затухания колебаний этой системы равен ….

22. Собственные колебания системы описываются уравнением движения: x¢¢+x=0. При

воздействии на систему периодической силы с амплитудой 4 Н, резонанс будет

наблюдаться на частоте ….

23. Собственные колебания системы описываются уравнением движения: x’’+12x’+100x=0. Частота её колебаний равна ….

Раздел 12. Волны

1. Звуковая волна – это ….

a. направленное движение частиц среды

b. процесс, происходящий с некоторой долей повторяемости

c. повторяющееся согласованное движение частиц среды

d. колебания частиц среды

2. Функция, описывающая распространение волны, выглядит следующим образом a

3. Волновое число равно ….

a. числу колебаний происходящих в некоторой точке пространства в единицу времени

b. расстоянию, на которое распространяется волна за один период

c. длине волнового периода

d. коэффициенту, стоящему перед координатой в выражении, определяющем фазу волны

4. Волновое число связано с длиной волны следующим соотношением:

5. Волновая поверхность – это ….

a. передняя граница волны

b. график волновой функции

c. геометрическое место точек волны, имеющих одинаковую фазу

d. плоскость, в которой происходят колебания частиц среды

6. Фронт волны – это ….

a. геометрическое место точек волны, имеющих одинаковую фазу

b. передняя волновая поверхность, наиболее удалённая от источника волны

c. график волновой функции

d. плоскость, в которой происходят колебания частиц среды

a. геометрическое место точек волны, имеющих одинаковую фазу

b. линия, вдоль которой распространяется энергия волны

c. передняя волновая поверхность, наиболее удалённая от источника волны

d. направление, в котором происходят колебания частиц среды

8. Фаза волны равна . d

9. Фазовая скорость распространения волны равна.

10. Групповая скорость распространения волн равна.

11. Интенсивность звуковой волны ….

a. – это мощность, переносимая волной через единичную поверхность,

перпендикулярную направлению её распространения

b. – это мощность, переносимая волной через единичную поверхность,

перпендикулярную направлению распространения волны, в единицу времени

c. равна её амплитуде

d. равна квадрату её амплитуды

12. Интенсивность звуковой волны при прочих равных условиях … плотности среды.

a. обратно пропорциональна

b. немонотонно зависит от

d. не зависит от

13. Интенсивность звуковой волны ….

a. пропорциональна квадрату амплитуды колебаний

b. пропорциональна амплитуде колебаний

c. обратно пропорциональна амплитуде колебаний

d. никак не связана с амплитудой колебаний

14. Интенсивность звуковой волны ….

a. пропорциональна частоте её колебаний

b. пропорциональна квадрату частоты её колебаний

c. обратно пропорциональна частоте её колебаний

d. не зависит от частоты колебаний

15. Бегущая волна отличается от стоячей тем, что у неё … меняется со временем.

a. направление распространения

b. частота колебаний

c. волновое число

d. можно определить поверхности постоянной фазы, положение которых

16. Поперечные колебания происходят в направлении ….

a. параллельном направлению распространения волны

b. перпендикулярном волновой поверхности

c. перпендикулярном поверхности постоянной фазы

d. перпендикулярном направлению распространения волны

17. Распространение волны описывается выражением: 6cos(2000t+5x+1000). Её волновое число равно ….

18. Распространение волны описывается выражением: 6cos(2000t+5x+1000). Её фазовая скорость равна ….

19. Длина волны 1 м, циклическая частота 800 с -1 , а волновое число равно ….

20. Распространение волны описывается выражением: 6cos(2000t+5x+1000). Фаза этой волны в точке x=200 м в момент времени t=1 c. равна ….

21. Распространение волны описывается выражением: 6cos(2000t+5x+1000). Её интенсивность 2 Вт/м 2 . При возрастании амплитуды волны в 2 раза её интенсивность становится равной ….

22. Распространение волны описывается выражением: 6cos(2000t+5x+1000). Её циклическая частота равна ….

23. Распространение волны описывается выражением: 6cos(2000t+5x+1000). Её длина равна ….

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Циклическая частота колебаний

Мерой колебательного движения служит циклическая (или угловая, или круговая) частотой колебаний.

Это скалярная физическая величина.

Видео:Колебательное движение. Свободные колебания | Физика 9 класс #23 | ИнфоурокСкачать

Циклическая частота при гармонических колебаниях

Пусть колебания совершает материальная точка. При этом материальная точка через равные промежутки времени проходит через одно и то же положение.

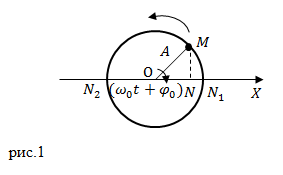
Самыми простыми колебаниями являются гармонические колебания. Рассмотрим следующую кинематическую модель. Точка M с постоянной по модулю скоростью ($v$) движется по окружности радиуса A. В этом случае ее угловую скорость обозначим $_0$, эта скорость постоянна (рис.1).

Проекция точки $M$ на диаметр окружности (точка $N$), на ось X, выполняет колебания от $N_1$ до $N_2 $и обратно. Такое колебание N ,будет гармоническим. Для описания колебания точки N необходимо записать координату точки N, как функцию от времени ($t$). Пусть при $t=0$ радиус OM образует с осью X угол $_0$. Через некоторый промежуток времени этот угол изменится на величину $_0t$ и будет равен $_0t+_0$, тогда:

Выражение (1) является аналитической формой записи гармонического колебания точки N по диаметру $N_1N_2$.

Обратимся к выражению (1). Величина $A$ — это максимальное отклонение точки, совершающей колебания, от положения равновесия (точки О — центра окружности), называется амплитудой колебаний.

Параметр $_0$ — циклическая частота колебаний. $varphi =(_0t+_0$) — фаза колебаний; $_0$ — начальная фаза колебаний.

Циклическую частоту гармонических колебаний можно определить как частную производную от фазы колебаний по времени:

При $_0=0$, уравнение колебаний (1) преобразуется к виду:

Если начальная фаза колебаний равна $_0=frac$ , то получим уравнение колебаний в виде:

Выражения (3) и (4) показывают, что при гармонических колебаниях абсцисса $x$ — это функция синус или косинус от времени. При графическом изображении гармонических колебаний получается косинусоида или синусоида. Форма кривой определена амплитудой колебаний и величиной циклической частоты. Положение кривой зависит от начальной фазы.

Циклическую частоту колебаний можно выразить через период (T) колебаний:

Циклическую частоту с частотой $?$$?$ свяжем выражением:

Единицей измерения циклической частоты в Международной системе единиц (СИ) является радиан, деленный на секунду:

Размерность циклической частоты:

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Частные случаи формул для вычисления циклической частоты

Груз на пружине (пружинный маятник — идеальная модель) совершает гармонические колебания с круговой частотой равной:

$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.

Малые колебания физического маятника будут приблизительно гармоническими колебаниями с циклической частотой равной:

где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.

Примером физического маятника является математический маятник. Круговая частота его колебаний равна:

где $l$ — длина подвеса.

Угловая частота затухающих колебаний находится как:

где $delta $ — коэффициент затухания; в случае с затуханием колебаний $_0$ называют собственной угловой частотой колебаний.

Видео:Урок 333. "Энергетический" метод расчета частоты свободных колебанийСкачать

Примеры задач с решением

Задание: Чему равна циклическая частота гармонических колебаний, если максимальная скорость материальной точки равна $<dot>_=10 frac$, а ее максимальное ускорение $<ddot>_=100 frac$?

Решение: Основой решения задачи станет уравнение гармонических колебаний точки, так как из условий, очевидно, что они происходят по оси X:

Скорость колебаний найдем, используя уравнение (1.1) и кинематическую связь координаты $x$ и соответствующей компоненты скорости:

Максимальное значение скорости (амплитуда скорости) равна:

Ускорение точки вычислим как:

Из формулы (1.3) выразим амплитуду, подставим ее в (1.5), получим циклическую частоту:

Вычислим циклическую частоту:

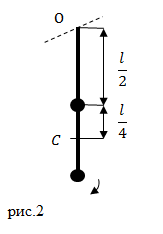
Задание: На длинном невесомом стержне закреплены два груза одинаковой массы. Один груз находится на середине стержня, другой на его конце (рис.2). Система совершает колебания около горизонтальной оси, проходящей через свободный конец стрежня. Какова циклическая частота колебаний? Длина стержня равна $l$.

Решение: Основой для решения задачи является формула нахождения частоты колебаний физического маятника:

где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника. Масса маятника по условию задачи состоит из масс двух одинаковых шариков (масса одного шарика $frac$). В нашем случае расстояние $a$ равно расстоянию между точками O и C (см. рис.2):

Найдем момент инерции системы из двух точечных масс. Относительно центра масс (если ось вращения провести через точку C), момент инерции системы ($J_0$) равен:

Момент инерции нашей системы относительно оси, проходящей через точку О найдем по теореме Штейнера:

Подставим правые части выражение (2.2) и (2.4) в (2.1) вместо соответствующих величин:

Видео:Колебательное движение. 1 часть. 9 класс.Скачать

Тесты по физике на тему: «Механические колебания.Упругие волны»

тесты по физике по теме «Механические колебания.Упругие волны2

Просмотр содержимого документа
«Тесты по физике на тему: «Механические колебания.Упругие волны»»

Тесты по теме: «Механические колебания. Упругие волны»

1. На рис. представлен график колебания груза на пружине. Чему равен период колебаний груза?

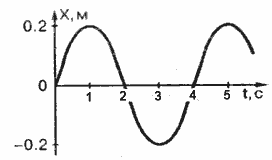
1)1с; 2)2с; 3)3с; 4)4с; 5) Среди данных ответов нет правильного.

2. Уравнение скорости маятника записывается уравнением: v_x=Cos 2t. Чему равна амплитуда скорости?

1)1м/с; 2)2м/с; 3) Cos2t; 4) 2t; 5) Среди ответов нет правильного.

3.Период колебаний математического маятника равен 0,5 с. Чему равна циклическая частота маятника?

1)0,5 с -1 2)2 с -1 3)4п с -1 4)1п с -1 5)Среди данных ответов нет правильного.

4. При гармонических колебаниях координата тела меняется по закону: x=0,4Sin2t (м). Чему равно наибольшее ускорение тела?

1) 0,4 м/с 2 ; 2) 0,2 м/с 2 3) 0,1 м/с 2 4) 0,8м/с 2 ; 5) 1,6 м/с 2 ;

5. Груз массой m, подвешенный на пружине, совершает колебания. Во сколько раз отличается частота колебаний груза массой 4m, подвешенного на той же пружине, от частоты первого груза?

1) в 4 раза меньше ; 2) в 2 раза меньше); 3) не отличается 4) в 2 раза больше

5) в 4 раза больше;

6. Как изменится частота математического маятника, если его длину увеличить в 4 раза?

1) Не изменится ; 2) Увеличится в 2 раза; 3) Увеличится в 4 раза; 4) Уменьшится в 2 раза; 5) Уменьшится в 4 раза;

7. Движение маятника описывается уравнением: x=2Sin t (м). Какой из графиков выражает зависимость координаты маятника от фазы колебаний?

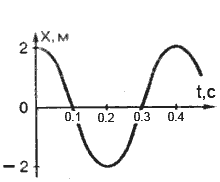
1)1 ; 2)2; 3)3; 4)4; 5) Ни один из графиков

8. При гармонических колебаниях координата х меняется по закону: x=0,6sin 3t (м). Чему равна амплитуда скорости?

1) 0,6 м/с ;2) 0,2 м/с;3) 1,8 м/с;4) 5,4 м/с;5) Среди данных ответов нет правильного;

9. Наибольшее значение кинетической энергии математического маятника 20 Дж. Как меняется его полная энергия при движении маятника вправо?

1) От 0 до 20 Дж ;2) 0 до 40 Дж;3) Не изменяется;4) От 20 до 0 Дж;5) От 40 до 0 Дж;

10. Колебания каких систем являются свободными: 1-математический маятник, 2-поршень двигателя, 3-груз на пружине, 4-струна гитары

1)3 ; 2)1 и 4; 3)2 и 3; 4)1 и 3; 5) Среди данных ответов нет правильного;

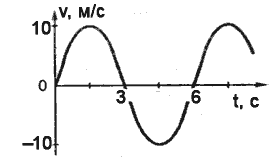
1. На рис. представлен график скорости колебаний груза. Чему равна амплитуда скорости груза?

1) 10 м/с; 2) 60 м/с; 3) 3 м/с; 4) 8 м/с; 5) Среди этих ответов нет правильного;

2. Колебания маятника описываются уравнением: x=2Sin 10t (м). Чему равна циклическая частота колебаний маятника?

1) 2с -1 ; 2) 10t с -1 ; 3) 10 с -1 ; 4) Sin10t с -1 ; 5) Среди этих ответов нет правильного;

3. Колебания груза происходят с циклической частотой 12,56 1/с. Чему равен период колебаний груза?

1) 0,5 с;2) 2 с;3) 12,56 с;4) 78,88 с;5) Среди этих ответов нет правильного;

4. При гармонических колебаниях ускорение груза меняется по закону: a_x=4Cos 2t (м/с2). Чему равна амплитуда координаты тела?

1) 16 м;2) 8 м;3) 4м;4) 2 м;5)1м;

5. Груз, подвешенный на пружине жесткостью k, совершает колебания. Во сколько раз изменится циклическая частота колебаний груза, если его подвесить на пружине с жесткостью 4k

1) Увеличится в 4 раза; 2) Увеличится в 2 раза; 3) Уменьшится в 2 раза;

4) Уменьшится в 4 раза; 5) Не изменится;

6. Как изменится период колебаний маятника, если его длину уменьшить в 4 раза?

1) Уменьшится в 2 раза;2) Уменьшится в 4 раза;3) Не изменится;4) Увеличится в 2 раза;5) Увеличится в 4 раза;

7. Движение маятника описывается уравнением: x=0,1Cos 4пt (м). Какой из приведенных внизу графиков выражает зависимость координаты маятника от фазы?

1)1; 2)2; 3)3; 4)4; 5) Ни один из этих графиков

8. При гармонических колебаниях координата груза меняется по закону: x=2Cos 3t (м). Чему равна амплитуда ускорения?

1) 54 м/с 2 ; 2) 18 м/с 2 ; 3) 6 м/с 2 ; 4) 2м/с 2 ; 5) Среди этих ответов нет правильного;

9. При гармонических колебаниях наибольшая потенциальная энергия пружины равна 50 Дж, наибольшая кинетическая энергия груза 50 Дж. Как меняется полная энергия маятника во время одного колебания?

1) От 0 до 50 Дж; 2) От 0 до 100Дж; 3) Не изменяется и равна 100 Дж;

4) Не изменяется и равна 50 Дж; 5) Среди этих ответов нет правильного;

10. Колебания каких тел являются вынужденными: 1-математического маятника, 2- поршень двигателя, 3-груз на пружине, 4-вибрации электродвигателя.

1)4; 2) 1 и 3; 3) 1 и 3; 4) 2 и 4; 5) Среди этих ответов нет правильного;

1. На рис. представлена зависимость координаты маятника от времени. Чему равна частота колебаний маятника?

1) 10 Гц; 2)5 Гц); 3) 3,З Гц; 4) 2,5 Гц; 5) Среди этих ответов нет правильного;

2. Колебания груза на пружине описываются уравнением: x=3Cos (2t+п/2) (м). Укажите фазу колебаний.

1)3; 2) 2t+п/2; 3) 2t; 4) 2п; 5) п/2;

3. Период колебаний груза на пружине равен 2 с. Чему равна циклическая частота колебаний груза?

1) 2 с -1 ; 2) 0,5 с -1 ; 3) 4п с -1 ; 4) п с -1 ; 5) Среди ответов нет правильного;

4. Координата колеблющегося груза меняется по закону: x=0,9Sin 3t (м). Чему равна амплитуда ускорений груза?

1) 0,1 м/с 2 ;2) 0,3 м/с 2 ;3) 0,9 м/с 2 ;4) 2,7м/с 2 ;5) 8,1 м/с 2 ;

5. Груз массой m, подвешенный на пружине совершает колебания с периодом Т₁. Чему равен период колебаний T₂ груза массой 4m на той же пружине?

6. Как изменится период колебаний пружинного маятника, если массу груза увеличить в 4 раза?

1) Увеличится в 4 раза;2) Увеличится в 2 раза;3) Не изменится;4) Уменьшится в 2 раза;5) Уменьшится в 4 раза;

7. Изменение скорости маятника описывается уравнением: v_x= -2Sin 2пt. Какой из приведенных внизу графиков показывает зависимость скорости этого маятника от времени?

1)1; 2)2; 3)3; 4)4; 5) Ни один из этих графиков;

8. Координата маятника меняется по закону: x=0,01Sin 10t (м). Чему равна амплитуда скорости маятника?

10,01 м/с); 2) 1 м/с;3) 0,1 м/с;4) 0,001 м/с;5) Среди этих ответов нет правильного;

9. При гармонических колебаниях тела на пружине наибольшее значение кинетической энергии равно 30 Дж. Чему равна максимальная потенциальная энергия пружины?

1) 0 Дж; 2) 15 Дж; 3) 30 Дж; 4) 60 Дж; 5) Среди этих ответов нет правильного;

10. Какие из перечисленных здесь колебаний нужно отнести к автоколебаниям: 1-математический маятник, 2-поршень двигателя, 3-маятник часов, 4-груз на пружине?

1)3;2) 1 и 4;3) 2 и 3;4) 2;5) Среди этих ответов нет правильного

1. На рис.1 представлен график колебаний маятника. Чему равна амплитуда координаты маятника?

1) 0,1 м ; 2) 0,2 м ; 3) 0,З м; 4) -0,З м; 5) Среди этих ответов нет правильного;

2. Скорость тела задана уравнением: v_x=5Sin (3t+п/3). Чему равна начальная фаза колебаний скорости?

1)5; 2) 3t+п/3; 3) 3t; 4) п/3; 5) Среди этих ответов нет правильного;

3. Колебания тела происходят с циклической частотой 4п с -1 . Чему равен период колебаний тела?

1) 0,5 с; 2) 2 с; 3) 2п ; 4) 2п; 5) Среди этих ответов нет правильного;

4. Ускорение тела при колебаниях меняется по закону: ax=9Cos 3t, (м/с2). Чему равна амплитуда координаты тела?

1) 1 м; 2) 3 м; 3) 9 м; 4) 27 м; 5) 81 м;

5. Груз, подвешенный на пружине жесткостью k, совершает колебания с периодом Т₁. Чему равен период Т₂ колебаний того же груза на пружине жесткостью 4к?

6. Как изменится период колебаний математического маятника, если массу груза увеличить в 4 раза?

1) Уменьшится в 4 раза; 2) Уменьшится в 2 раза; 3) Не изменится;

4) Увеличится в 2 раза; 5) Увеличится в 4 раза;

7. Ускорение тела меняется по закону: a_x=8Cos 4пt, (м/с2). Какой из графиков, приведенных внизу, показывает зависимость ускорения этого маятника от фазы?

1)1; 2)2; 3)3; 4)4; 5) Ни один из этих графиков;

8. Тело массой 2 кг совершает колебания согласно уравнению: a_x=3Sin 100t, (м/с2). Какова амплитуда силы, приложенной к телу?

1) 300 Н; 2) 3 Н ; 3) 6 Н; 4) 200 Н;5) 600 Н;

9. При гармонических колебаниях максимальное значение потенциальной энергии тела 10 Дж. Чему равно наибольшее значение кинетической энергии тела?

1) 0 Дж; 2) 5 Дж; 3) 10 Дж; 4) 20 Дж; 5) Среди этих ответов нет правильного;

10. Какие из перечисленных здесь колебаний являются незатухающими: 1-груз на пружине, 2-математический маятник, 3-маятник часов, 4-поршень двигателя?

1) 1 и 2; 2) 3 и 4; 3) 1,2 и З; 4) 2,3 и 4; 5) Все примеры;

За каждый правильный ответ присваивается один балл, в сумме необходимо набрать 10 баллов из 10 задании. Оценивание работы будет высчитываться в процентном соотношении, где:

100% (10 -баллов) — отметка «5»

90% — 80% (9-8 баллов) — отметка «4»

70% — 60% ( 7-6баллов) — отметка «3»

менее 50% (менее 5 баллов)- отметка «2» с последующей пересдачей, но при этом окончательный отметка будет на балл ниже.

🎥 Видео

Урок 327. Гармонические колебанияСкачать

Собственные частоты колебаний точкиСкачать

Затухающие колебания. Вынужденные колебания | Физика 9 класс #26 | ИнфоурокСкачать

Величины, характеризующие колебательное движение | Физика 9 класс #24 | ИнфоурокСкачать

Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Урок 325. Колебательное движение и его характеристикиСкачать

71. Вынужденные колебанияСкачать

Выполнялка 53.Гармонические колебания.Скачать

Вынужденные колебания. Резонанс | Физика 11 класс #9 | ИнфоурокСкачать

Гармонические колебания | Физика 11 класс #8 | ИнфоурокСкачать

Физика 9 класс. §24 Величины, характеризующие колебательное движениеСкачать

Урок 343. Затухающие колебания (часть 1)Скачать

Превращение энергии при колебаниях. Уравнение колебательного движения. 1 часть. 9 класс.Скачать

Гармонические колебанияСкачать