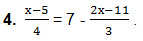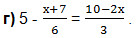Соберу схему для левой части уравнения

Вопрос по алгебре:

Помогите пожалуйста решите задание с сайта учи ру

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Соберите в левой части уравнения — 4x + 3, 6 + 3x — 2?

Математика | 5 — 9 классы

Соберите в левой части уравнения — 4x + 3, 6 + 3x — 2.

1 все слагаемые содержащие неизвестное, а в правой — не содержавшие неизвестное.

Видео:Вспоминаем схему Горнера и уравнения высших степенейСкачать

Решите срочно?

Решите уравнения по следующему плану : 1)Перенесите числа в одну часть уравнения, а слагаемые, содержащие неизвестные, — в другую, изменив при этом знаки слагаемых на противоположные ; 2)Упростите уравнения ; 3)Разделите обе части уравнения на коэффициент при неизвестном ; 1)10х + 23 = 9х + 19 ; 2)7у — 19 = 5 — 5у ; 3) — 5х — 7 = 3х + 13 ;

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Перенесите слагаемые, содержащие неизвестное, в левую часть уравнения, а все остальные слагаемые — в правую , затем приведите подобные слагаемые?

Перенесите слагаемые, содержащие неизвестное, в левую часть уравнения, а все остальные слагаемые — в правую , затем приведите подобные слагаемые.

0, 5x — 2y = 4 — y 2, 4x + 1, 5 = — 2x + 0, 3.

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

1)Равенсво содержащее неизвестное2)?

1)Равенсво содержащее неизвестное

Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Выпиши и реши по два уравнения с неизвестным вычитаемым, с неизвестным уменьшаемым, с неизвестным слагаемым?

Выпиши и реши по два уравнения с неизвестным вычитаемым, с неизвестным уменьшаемым, с неизвестным слагаемым.

Видео:Как решать уравнения по схеме ГорнераСкачать

Перенесите слагаемые, содержащие неизвестное, в левую часть уравнения, а все остальные слагаемые в правую?

Перенесите слагаемые, содержащие неизвестное, в левую часть уравнения, а все остальные слагаемые в правую.

Найдите корень уравнения.

В) — 12n — 24 = 11n — 24.

Г) 3x — 45 + 2x = 6 + 2x — 45.

Видео:Кубические уравнения. Деление столбиком. Схема Горнера.Скачать

Соберите в левой части уравнения 6х — 1, 3 = — 2х + 2, 2 все слагаемые, содержащие неизвестное, a в правой — не содержащие неизвестное?

Соберите в левой части уравнения 6х — 1, 3 = — 2х + 2, 2 все слагаемые, содержащие неизвестное, a в правой — не содержащие неизвестное.

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Выполните перенос слагаемых, содержащих неизвестное , в левую часть уравнения 7y = 3y — 9y + 21?

Выполните перенос слагаемых, содержащих неизвестное , в левую часть уравнения 7y = 3y — 9y + 21.

Видео:Матричный метод решения систем уравненийСкачать

Соберите в левой части уравнения — 4х + 3, 6 = 3х — 2, 1 все слагаемые, содержащие неизвестное, а в правой — не содержащие неизвестное?

Соберите в левой части уравнения — 4х + 3, 6 = 3х — 2, 1 все слагаемые, содержащие неизвестное, а в правой — не содержащие неизвестное.

Видео:8.1 Решение уравнения теплопроводности на отрезкеСкачать

РЕшите уравнение 4х — 9 = 7х + 6 способом переносом всех слагаемых в левую часть 2 способом переносом слагаемых содержащих переменную в левую часть а не содержащих переменной в правую часть?

РЕшите уравнение 4х — 9 = 7х + 6 способом переносом всех слагаемых в левую часть 2 способом переносом слагаемых содержащих переменную в левую часть а не содержащих переменной в правую часть.

Видео:Решение уравнений. Как переносить слагаемые из одной части уравнения в другую. Математика 6 классСкачать

Чтобы решить уравнение 4х — 8 = х + 1, в его левой части собрали все слагаемые, содержащие неизвестное, а в правой части — все слагаемые, не содержащие неизвестное?

Чтобы решить уравнение 4х — 8 = х + 1, в его левой части собрали все слагаемые, содержащие неизвестное, а в правой части — все слагаемые, не содержащие неизвестное.

Укажите верный результат.

1)4х + х = 1 — 8 2)4х — х = 1 + 8 3)4х — х = 1 — 8 4)4х + х = 1 + 8.

На этой странице находится ответ на вопрос Соберите в левой части уравнения — 4x + 3, 6 + 3x — 2?, из категории Математика, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

85 / 100 = 17 * 5 / 20 * 5 = 17 / 20 17 / 20 : 5 / 24 = 17 / 20 * 24 / 5 17 / 20 * 5 / 24 = 17 * 24 / 20 * 5 = 408 / 100 408 / 100 = 102 * 4 / 25 * 4 = 102 / 25 102 / 25 = 2 + 4 * 25 / 25 = 4 в числителе 2 в знаменателе 25 ВОТ ТАК У ТОГО ПАЦАНА НЕ ПР..

85 / 100 : 5 / 24 = 4. 08 получится.

1) 150 — 58 = 92 земля дальше чем меркурий на 92 млн км 2) 228 — 108 = 120 венера ближе чем марс на 120 млн км все.

На сколько : 1)Дальше от Солнца Земля, чем Меркурий? 150 — 58 = 92 2)Ближе к Солнцу Венера, чем Марс? 228 — 108 = 120.

1) 20 кг — 16 кг пюре 45 кг — ? Кг пюре (20 + 20) + (16 : 2) = 40 + 8 = 48(кг) пюре 2) 3м — 5дней 5м — ? Дней (5 — 3) + 5 = 7 (дней) за 7 дней закончат маляры работу 3) 1 / 2 — 50км / ч ? — 100км / ч 1 / 2 + 1 / 2 = 2 / 4(мин. ) фигню какую то на..

Функция, построение. Смотри файл.

Смотрите решение во вложении.

(9, 2 + 27 1 / 4) : 5, 4 + (18 3 / 25 — 9, 88) : 10, 3 = (9. 2 + 67. 75) : 5. 4 + (7. 32 — 9. 88) : 10. 3 = 14. 25 — 0. 25 = 14.

33 12 9 38 83 26 49 34 50 29 26 55 100 43 66 51 45 62 a + 17 a — 17.

Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

6.5.1. Линейное уравнение с одной переменной

У очень многих школьников возникает вопрос — как решить уравнение с x. Что значит решить уравнение и как найти корень уравнения. Давайте рассмотрим основную схему решения обычного уравнения, называемого линейным, с одной переменной.

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Правила и определения

Основные правила и определения для линейного уравнения с одной переменной.

• Равенство с переменной называют уравнением.
• Решить уравнение – значит найти множество его корней. Уравнение может иметь один, два, несколько, множество корней или не иметь их вовсе.
• Каждое значение переменной, при котором данное уравнение превращается в верное равенство, называется корнем уравнения.
• Уравнения, имеющие одни и те же корни, называются равносильными уравнениями.
• Любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
• Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Видео:Уравнения. Вебинар | МатематикаСкачать

Примеры. Решить уравнение.

Уравнение 1

1. 1,5х-0,3х = -2-4. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
2. 1,2х = -6. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
3. х = -6 : 1,2. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.
4. х = -5. Делили по правилу деления десятичной дроби на десятичную дробь:
5. чтобы разделить число на десятичную дробь, нужно перенести запятые в делимом и делителе на столько цифр вправо, сколько их стоит после запятой в делителе, а затем выполнить деление на натуральное число: 6 : 1,2 = 60 : 12 = 5.

Ответ: 5.

Уравнение 2

3∙(2х-9) = 4∙(х-4).

1. 6х-27 = 4х-16. Раскрыли скобки, используя распределительный закон умножения относительно вычитания: чтобы разность двух чисел умножить на третье число, можно отдельно уменьшаемое и отдельно вычитаемое умножить на третье число, а затем из первого результата вычесть второй результат, т.е. (a-b) ∙ c = a ∙ c-b ∙ c.
2. 6х-4х = -16+27. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
3. 2х = 11. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
4. х = 11 : 2. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: 5,5.

Уравнение 3

1. 7х-3-2х = х-9. Раскрыли скобки по правилу раскрытия скобок, перед которыми стоит знак «-»: если перед скобками стоит знак «-», то убираем скобки, знак «-» и записываем слагаемые, стоявшие в скобках, с противоположными знаками.
2. 7х-2х-х = -9+3. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
3. 4х = -6. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
4. х = -6 : 4. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: -1,5.

Уравнение 4

1. 3 ∙ (х-5) = 7 ∙ 12 — 4 ∙ (2х-11). Умножили обе части равенства на 12 – наименьший общий знаменатель для знаменателей данных дробей.
2. 3х-15 = 84-8х+44. Раскрыли скобки, используя распределительный закон умножения относительно вычитания: чтобы разность двух чисел умножить на третье число, можно отдельно уменьшаемое и отдельно вычитаемое умножить на третье число, а затем из первого результата вычесть второй результат, т.е. (a-b) ∙ c = a ∙ c-b ∙ c.
3. 3х+8х = 84+44+15. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
4. 11х = 143. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
5. х = 143 : 11. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: 13.

Видео:Классический способ решения Диофантовых уравнений ➜ Решите уравнение в целых числах ➜ 13x-7y=6Скачать

Уравнения для самостоятельного решения

Решить самостоятельно уравнения:

а) 3-2,6х = 5х+1,48;

б) 1,6 · (х+5) = 4 · (4,5-0,6х);

в) 9х- (6х+2,5) = — (х-5,5);

5а) 0,2; 5б) 2,5; 5в) 2; 5г) -1.

Видео:Контрольная работа. Уравнения с МОДУЛЕМСкачать

Важные выводы

Итак, для того, чтобы решить уравнение — надо определить его переменную, перенести неизвестную переменную в левую часть уравнения, а известные — в праву. При необходимости упростить левую и правую части и затем найти корень уравнения.

📹 Видео

Как решить линейное уравнение с дробями. Пример 1Скачать

Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать

Ионные уравнения реакций. Как составлять полные и сокращенные уравненияСкачать

Проверь себя ➜ реши задачу!Скачать