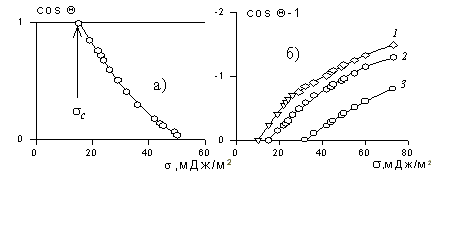Смачивание несмачивание растекание уравнение юнга (5 видео)

ГЛАВА ХI. АДГЕЗИЯ, СМАЧИВАНИЕ И РАСТЕКАНИЕ ЖИДКОСТЕЙ

Адгезия и работа адгезии

Адгезия, смачивание и растекание относятся к межфазным взаимодействиям, которые происходят между конденсированными фазами. Межфазное взаимодействие или взаимодействие между приведенными в контакт поверхностями конденсированных тел разной природы называют адгезией(прилипанием). Адгезия обеспечивает между двумя телами соединение определенной прочности, обусловленное межмолекулярными силами.

Различают адгезию между двумя жидкостями, между жидкостью и твердым телом и между двумя твердыми телами.

Явления адгезии и смачивания широко распространены. Склеивание материалов, нанесение покрытий, получение материалов на основе связующих и наполнителей (бетон, резина, стеклопластики и т. п.), сварка и паяние металлов, печатание – все эти процессы связаны с адгезией и смачиванием, которые в значительной степени определяют качество материалов и изделий.

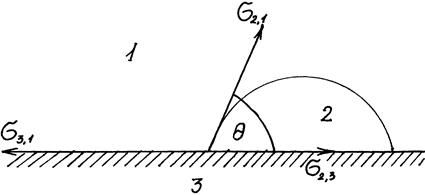
Рис.27. К выводу соотношения между работой адгезии и поверхностными натяжениями взаимодействующих компонентов (уравнения Дюпре): 1 – газ; 2 – жидкость; 3 ‑ твердое тело

Из-за сложности протекающих процессов, рассматриваемые в данном разделе межфазные явления до сих пор недостаточно изучены. Поэтому основное внимание будет уделено системам, в которых имеется хотя бы одна жидкая фаза, что позволяет обеспечивать равновесные обратимые условия и соответственно использовать термодинамические соотношения.

Адгезия – результат стремления системы к уменьшению поверхностной энергии. Поэтому адгезия является самопроизвольным процессом.

Работа адгезии W_ад (по аналогии с работой когезии) определяется как работа изотермического обратимого разделения двух конденсированных фаз вдоль межфазной поверхности единичной площади.

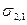
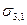
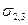
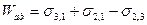
При таком разделении образуются свободные поверхности раздела обеих конденсированных фаз с газом, имеющие энергии и , и исчезает межфазная поверхность с энергией (рис.27), следовательно,

(XI.1)

Это уравнение Дюпре. Оно отражает закон сохранения энергии при адгезии. Из него следует, что работа адгезии тем больше, чем больше поверхностные натяжения исходных компонентов и чем меньше межфазное натяжение.

Величина W_ад характеризует родственность контактирующих фаз, т. е. степень насыщения нескомпенсированных поверхностных сил при контакте. Межфазная энергия 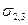, наоборот, определяет интенсивность остаточных нескомпенсированных сил на границе раздела конденсированных фаз.

Она измеряется в тех же единицах, что и поверхностное натяжение (Дж/м 2 ).

Работу адгезии экспериментально определяют при непосредственном разрушении соединения. Работу адгезии можно определить и косвенными методами, которые особенно удобны, если хотя бы одной из взаимодействующих фаз является жидкость и можно измерить, например, краевой угол.

Смачивание и краевой угол. Закон Юнга

Смачивание – это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом).

Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания), или просто краевым углом (углом смачивания).

При нанесении небольшого количества жидкости, например, капли на поверхность другой жидкости, имеющей большую плотность, или на поверхность твёрдого тела можно наблюдать два процесса, если приводимые в контакт вещества взаимно нерастворимы. В одном случае нанесенная жидкость остается на поверхности другой фазы в виде капли, принявшей при установившемся равновесии определенную форму. В другом случае капля растекается по поверхности. Вначале рассмотрим первый процесс, когда капля не растекается полностью по поверхности другого тела.

Рис.28. К выводу уравнения для краевого угла (закона Юнга).

Рис.28 иллюстрирует состояние капли жидкости на поверхности твёрдого тела в условиях равновесия. Поверхностная энергия твёрдого тела, стремясь уменьшиться, вызывает растяжение капли по поверхности. Эта энергия равна поверхностному натяжению твёрдого тела на границе с воздухом s_{3, 1}. Межфазная энергия на границе твёрдого тела с жидкостью s_{2, 3} стремится, наоборот, сжать каплю, т. е. поверхностная энергия уменьшается за счет снижения площади поверхности. Растеканию препятствуют когезионные силы, действующие внутри капли. Действие когезионных сил направлено от границы между твёрдой, жидкой и газообразной фазами по касательной к сферической поверхности капли и равно s_{2, 1} (силы гравитации не учитываются). Угол q, который образован касательными к межфазным поверхностям, ограничивающим смачивающую жидкость, имеющий вершину на линии раздела трех фаз, называется краевым углом смачивания.

Так как поверхностное натяжение можно рассматривать как энергию, приходящуюся на единицу площади, или как силу, действующую на единицу длины, то все рассмотренные составляющие поверхностной энергии можно выразить с помощью векторов сил. При равновесии между ними соблюдается следующее соотношение:

(XI.2)

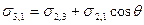
Полученное соотношение называется законом Юнга. Отсюда количественную характеристику смачивания – косинус краевого угла можно выразить через поверхностные и межфазное натяжения:

(XI.3)

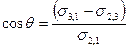
Чем меньше угол q и соответственно больше cos q, тем лучше смачивается поверхность. При остром угле q, т. е. при cos q > 0, поверхность считают хорошо смачиваемой данной жидкостью. Если угол q тупой, т. е. cos q

Содержание

Поверхностные явления и адсорбция
Тема 1. Поверхностные явления и адсорбция
ЛИТЕРАТУРА
НАГЛЯДНЫЕ ПОСОБИЯ И ПРИЛОЖЕНИЯ
Краевой угол смачивания
ВВЕДЕНИЕ
2.3.2. Смачивание и растекание на границе твердое тело – жидкость – газ
🎦 Видео

Видео:Смачивание. Капиллярные явления. 10 класс.Скачать

Поверхностные явления и адсорбция

Кандидат химических наук, доцент

Видео:Урок 13 (осн). Взаимодействие молекул. Смачивание и несмачиваниеСкачать

Тема 1. Поверхностные явления и адсорбция

Занятие 2. Поверхностные явления

2. Смачивание и растекание.

3. Основные понятия и характеристики адсорбции.

4. Изотермы и изобары адсорбции

Видео:Физика. Объяснение темы "Смачивание, несмачивание, капиллярность"Скачать

ЛИТЕРАТУРА

1. Фролов коллоидной химии. – М.: Химия, 1989. – С. 25-31, 78-96.

2. Коллоидная химия. – СПб.: «Лань», 2003. – С. 70-76.

Видео:Урок 12. Взаимодействие молекул. Смачивание и несмачиваниеСкачать

НАГЛЯДНЫЕ ПОСОБИЯ И ПРИЛОЖЕНИЯ

Работа когезии и адгезии

Видео:Опыты по физике. Смачивание и краевые углыСкачать

Краевой угол смачивания

Критерии смачивания и несмачивания

Видео:Урок 199. Смачивание. Капиллярные явленияСкачать

ВВЕДЕНИЕ

Изучение поведения жидкостей на твердых и жидких поверхностях представляет большой интерес в связи с широкой распространенностью явлений смачивания и растекания как в природе, так и в различных отраслях народного хозяйства. Явления смачивания и растекания лежат в основе процессов отмывания жидких загрязнений с твердых покрытий. Начнем с изучения понятий адгезии и когезии.

1. АДГЕЗИЯ И КОГЕЗИЯ

Когезия характеризует взаимное притяжение частиц (атомов, молекул) однородного тела, обусловленное силами межмолекулярного взаимодейст-вия, действующими внутри тела.

Когезия характеризует прочность тел на разрыв. Она сильна в твердых телах, меньше в жидкостях.

Адгезия характеризует взаимное притяжение частиц различных тел в области их соприкосновения (т. е. на поверхности раздела фаз), обусловленное силами межмолекулярного взаимодействия, действующими между этими телами.

Количественно когезия и адгезия характеризуются соответственно работой когезии Wк и работой адгезии Wa. Эти величины измеряются в тех же единицах, что и поверхностное натяжение (Дж/м2, Н/м), и они связаны с поверхностным натяжением (рис. 1).

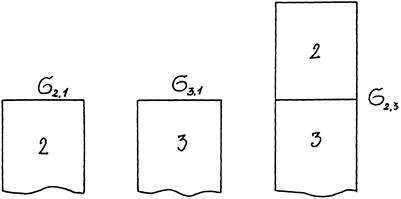
Работа когезии Wк – работа, которую надо совершить для разрыва однородного тела по сечению с единичной площадью на две части. Эта работа затрачивается на разрыв межмолекулярных связей внутри тела. Представим мысленно цилиндр из какой-либо жидкости с единичной площадью сечения S (рис. 1). Разорвем этот цилиндр на 2 части.

Смачивание несмачивание растекание уравнение юнга

Рис. 1. К выводу соотношения между когезией и

Образовалась новая поверхность площадью 2S на границе жидкость – газ. Если вспомнить физический смысл поверхностного натяжения (это работа, которую надо совершить, чтобы увеличить на единицу площадь поверхности раздела фаз), то можно записать

где Wк – работа когезии, Дж/м2;

sЖ-Г – поверхностное натяжение на границе раздела

жидкость – газ, Дж/м2.

При разрыве твердого тела на две части работа когезии соответственно равна

где sТ-Г – поверхностное натяжение на границе раздела

твердое тело – газ, Дж/м2.

сразу можно отметить, что работа когезии тем больше, чем больше величина поверхностного натяжения.

Работа адгезии Wa – работа, которую надо совершить для разрыва двух соприкасающихся тел с единичной площадью контакта. Эта работа затрачивается на разрыв межмолекулярных связей, возникающих на границе раздела фаз.

Рис. 2. К выводу соотношения между адгезией и

Пусть в соприкосновении находятся две несмешивающиеся жидкости с единичной площадью контакта. Граница раздела фаз характеризуется поверхностным натяжением sЖ1- Ж2. После разрыва исчезла граница раздела фаз ж1-ж2, но появились две новые площади поверхности, которые характеризуются поверхностным натяжением sЖ1- Г и sЖ2 — Г.

Очевидно, что работу адгезии можно рассчитать по формуле

Wa = sЖ1- Г + sЖ2 — Г – sЖ1- Ж2 (3)

Это выражение называется уравнением Дюпре.

По аналогии при отрыве жидкости от твердой поверхности совершается работа адгезии, равная:

Wa = sЖ — Г + sТ — Г – sТ — Ж (4)

По уравнению (3) работу адгезии вычислить достаточно легко, поскольку все входящие в него величины определяются экспериментально.

По уравнению (4) рассчитать Wа практически невозможно, т. к. определение поверхностного натяжения на границе с твердым телом представляет собой сложную экспериментальную задачу.

Силы когезии и адгезии играют большую роль в процессах смачивания и несмачивания жидкостями твердых тел, склеивания материалов, нанесения лакокрасочных и других покрытий, печатания, крашения.

2. СМАЧИВАНИЕ И РАСТЕКАНИЕ

Смачивание – это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом).

При нанесении капли жидкости на поверхность твердого тела (или другой жидкости) можно наблюдать разные явления. В одном случае нанесенная жидкость сохраняет форму капли, в другом случае капля растекается по поверхности. Рассмотрим первый случай (рис. 3)

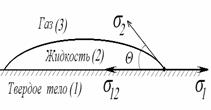
Рис. 3. Смачивание жидкостью твердого тела

Линия соприкосновения трех фаз называется периметром смачивания. Угол q называется краевым углом смачивания. Он отсчитывается со стороны жидкости. Поскольку капля находится в состоянии равновесия, действие сил на нее скомпенсировано. Рассмотрим эти силы. Как известно, силы поверхностного натяжения направлены на сокращение площади контакта фаз и действуют по касательной к поверхности. На рис. 3 эти силы представлены векторами, выходящими из точки соприкосновения всех трех фаз.

sТ-Г – стремиться уменьшить площадь контакта твердого тела с газом, поэтому растягивает пленку жидкости по твердому телу.

sТ-Ж – стремится уменьшить площадь контакта твердого тела с жидкостью, поэтому стягивает каплю жидкости в шарик.

sЖ-Г – стремится уменьшить площадь контакта жидкости с газом, поэтому стягивает каплю жидкости в шарик (шарообразная поверхность имеет наименьшую площадь).

Рассмотрим равнодействующую сил, действующих на каплю в точке О вдоль поверхности твердого тела. Эти силы поверхностного натяжения sТ-Г, sТ-Ж, а также проекция sЖ-Г на выбранную ось = sЖ-Г. cosq.

В состоянии равновесия равнодействующая сил равна 0:

sТ-Г = sТ-Ж + sЖ-Г. cosq (5)

Полученное соотношение (5) называется законом Юнга.

Краевой угол смачивания q или cosq являются количественной характеристикой смачивания. Чем меньше угол q и соответственно больше cosq, тем лучше смачивается поверхность.

Закон Юнга позволяет выразить cosq через поверхностные межфазные натяжения:

(6)

Сочетание уравнения Дюпре (4) с законом Юнга (5) позволяет выразить работу адгезии Wa через косинус краевого угла смачивания q.

Из уравнения (5) выразим разность

sТ-Г – sТ-Ж = sЖ-Г. cosq

Полученную разность подставим в уравнение 4

Wa = sЖ-Г + sЖ-Г. cosq = sЖ-Г(1 + cosq) (7)

Уравнение (7) называют уравнением Дюпре – Юнга. Оно позволяет рассчитать работу адгезии, если известно поверхностное натяжение жидкости и краевой угол смачивания. Обе эти величины сравнительно легко определяются экспериментально: q определяют путем проектирования капли на экран (с помощью несложной установки) и измерения краевого угла на проекции капли. С помощью уравнения Дюпре – Юнга (7) легко найти соотношение между работой когезии смачивающей жидкости и работой адгезии между жидкостью и смачиваемым телом.

Краевой угол смачивания (или косинус краевого угла) является характеристикой способности жидкости смачивать твердую или жидкую поверхность. В таблице 1 представлены возможные случаи поведения жидкости на твердой или жидкой поверхности. Смачивание или несмачивание зависит от соотношения работы когезии и работы адгезии.

Таблица 1. Критерии смачивания, несмачивания и растекания

q > 900 (тупой угол)

Смачивание жидкостью поверхности

Капиллярное поднятие или опускание жидкостей связано с возникновением кривизны поверхности (выпуклый или вогнутый мениск). В свою очередь появление кривизны поверхности связано с процессами смачивания (q 900, выпуклый мениск) жидкостями стенок капилляров.

Растекание жидкостей по поверхности

Особо остановимся на предельном случае смачивания – растекании жидкости по поверхности, которое наблюдается при q = 00, когда работа адгезии равна работе когезии (Wa = Wк). Очевидно, что чем больше преобладает работа адгезии над работой когезии, тем лучше будет растекаться жидкость по поверхности. Величина

называется коэффициентом растекания или критерием Гаркинса.

Если f > 0 – жидкость растекается (Wa > Wк)

Изотермы полимолекулярной адсорбции (рис.7) характерны для адсорбции газов и паров на твердых адсорбентах. Изотерма вида а (s-образная изотерма) при невысоких давлениях напоминает изотерму мономолекулярной адсорбции (участок Р1), т. е. на поверхности образуется один слой молекул адсорбтива. При дальнейшем увеличении давление газа на первый слой может сесть второй, третий и т. д. слой молекул, происходит полимолекулярная адсорбция, поэтому адсорбция резко возрастает.

Первый слой молекул удерживается на адсорбенте силами взаимодействия адсорбент — адсорбтив, а второй, третий слои удерживаются силами притяжения между молекулами адсорбтива. Концентрирование адсорбтива на поверхности приводит к тому, что газ (пар) конденсируется и образуется жидкий слой конденсата на поверхности адсорбента.

Рис.7. Изотермы полимолекулярной адсорбции

Рs – давление насыщенного пара

Изотермы адсорбции с капиллярной конденсацией (рис.8) характерны для газов (паров), адсорбирующихся на пористых адсорбентах. Эти изотермы сходны с изотермами полимолекулярной адсорбции, но имеют и некоторые отличия. Пористые адсорбенты имеют многочисленные поры, которые представляют из себя капилляры. При образовании полимолекулярного слоя на стенках пор возникает искривленная (вогнутая) поверхность раздела фаз жидкость – пар, давление насыщенного пара над которой меньше, чем над плоской поверхностью. Поэтому в пористых материалах пар конденсируется при более низких давлениях и конденсация идет до заполнения всех пор. Этот процесс заканчивается раньше, чем достигается давление насыщенного пара. Поэтому изотерма адсорбции выходит на предельное значение (все поры заполнены, адсорбция не идет).

Рис.8. Изотермы полимолекулярной адсорбции,

осложненной капиллярной конденсацией

Рs – давление насыщенного пара

Изобары и изопикны адсорбции

Изобарой адсорбции называется зависимость величины адсорбции газа (или пара) на твердом адсорбенте от температуры при постоянном парциальном давлении газа (пара) А = fр(Т)

Изопикной адсорбции называется зависимость величины адсорбции растворенного вещества от температуры при постоянной концентрации растворенного вещества А = fc(Т)

Процесс адсорбции экзотермичен и, следовательно, в соответствии с принципом Ле-Шателье с ростом температуры величина физической адсорбции уменьшается (рис.9). При повышении температуры колебания адсорбированных поверхностью частиц усиливаются, они отрываются от поверхности, равновесие сдвигается в сторону процесса десорбции.

Рис.9. Изобара (Р = const) или изопикна (С = const) адсорбции.

Описание взаимодействия молекул адсорбтива и молекул адсорбента представляет собой весьма сложную и до сих пор до конца неразрешенную задачу. Рассмотрению некоторых теорий адсорбции будет посвящена следующая лекция.

Сегодня мы познакомились с основными видами поверхностных явлений: смачиванием, растеканием и адсорбцией. Следующая лекция будет посвящена подробному рассмотрению явлений адсорбции, которые играют значительную роль в природе, технологических процессах.

Видео:§ 6 Смачивание. Капиллярные явленияСкачать

2.3.2. Смачивание и растекание на границе твердое тело – жидкость – газ

В большинстве случаев жидкость на поверхности твердого тела остается в виде капли, большей или меньшей толщины, контактирующей с твердым телом под определенным углом, который называется краевым углом смачивания и обозначается буквой Q (рис. 1.24). Растекание капли по поверхности прекратится при достижении равновесия, которое без учета сил тяжести может быть описано уравнением Юнга:

(1.2.44)

, (1.2.45)

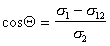
где индексы 1, 2, 3 – обозначают, соответственно, твердую, жидкую и газовую фазы.

Работа адгезии выражается уравнением Дюпре:

(1.2.46)

. (1.2.47)

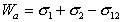
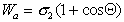
Рис. 1.24. Капля жидкости на поверхности твердого тела (схема)

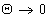
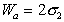
Работа адгезии при ,т.е. при полном смачивании, , что эквивалентно работе когезии жидкости. Если Q = 180 o , соs Q = -1 и в соответствии с уравнением (1.2.47) W_a = 0, т.е. жидкость не смачивает твердую поверхность. При Q» 90 o жидкость проявляет слабое смачивание.

Следует помнить, что определение работы адгезии в реальных системах предполагает равновесие фаз, насыщенных относительно друг друга.

Кроме того, твердая поверхность, по которой происходит растекание жидкости, не свободна. Она обычно покрыта пленкой вещества, адсорбированного из газо-паровой фазы. Эта пленка имеет поверхностное давление p, поэтому

, (1.2.48)

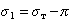
Смачивание неоднородных, пористых или шероховатых поверхностей сопровождается запиранием пузырьков воздуха в неровностях. В результате этого краевые углы смачивания сухой и предварительно увлажненной поверхностей различаются. Такое явление носит название «гистерезис смачивания». Гистерезис смачивания проявляется также при загрязнении поверхности, в результате чего она становится неоднородной при закреплении на ней твердых частиц или жировых пленок. В этом случае поверхность ведет себя как составная.

Шероховатость поверхности учитывается введением коэффициента шероховатости r, представляющего отношение площади поверхности реального тела к площади идеально гладкой поверхности, тогда

. (1.2.49)

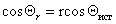
Можно отметить, что если краевой угол смачивания гладкой поверхности, например полимерной пленки, меньше 90 o , то шероховатость (ткань из волокон этого полимера) уменьшает его, если же он больше 90 o , то шероховатость его увеличивает. Для составной поверхности, которая специфична для большинства текстильных материалов, наличие участков различной природы может быть учтено введением коэффициентов x, характеризующих долю поверхности с различными свойствами. Например, если текстильный материал изготовлен из волокон двух видов 1 и 2, то

. (1.2.50)

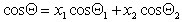
Если переплетение нитей таково, что получается сетчатый или дырчатый материал, то уравнение (2.50) принимает вид

, (1.2.50′)

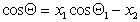
где х₂ – доля открытой поверхности.

Как мы обсуждали выше, поверхностное натяжение можно разделить на компоненты дисперсионных и полярных сил, а при нахождении межфазового натяжения для многих жидких границ можно ограничиться лишь дисперсионной составляющей. Такое ограничение позволяет провести обсуждение явления смачивания (по крайней мере, низкоэнергетических поверхностей, к каковым можно отнести подавляющее большинство волокнообразующих полимеров), в рамках теории дисперсионных сил.

Как показал Н. В. Чураев смачивание неполярной жидкостью твердой поверхности возможно, если будет соблюдаться условие смачивания, которое выражается уравнением

, (1.2.51)

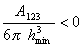
где А₁₂₃ – составная постоянная Гамакера при взаимодействии жидкости (фаза 2) с твердым телом (фаза 1) на границе с воздухом (фаза 3); h_m_in — наименьшая толщина пленки, которая фактически соответствует Ван-дер-Ваальсову расстоянию, т.е. h_m_in = (0,22¸0,24) нм. Например, для воды на поверхности тефлона А₁₂₃ = -7·10 — 21 Дж.

Учет только дисперсионных сил приводит к уравнению

, (1.2.52)

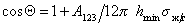
При расчетах углов смачивания твердых поверхностей следует учитывать поверхностное давление пленки, образованной при адсорбции из газо-паровой фазы. Тогда с учетом уравнения (1.2.48), уравнение Юнга (1.2.45) следует записать в виде

. (1.2.53)

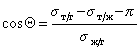
Способ расчета поверхностного давления предложили Бэнгхэм и Разорук:

, (1.2.54)

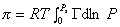
где P – равновесное давление, Г– равновесная адсорбция газа (пара), P_s – давление насыщения.

При больших углах смачивания и слабом взаимодействии жидкости с твердым телом поверхностное давление обычно не учитывают.

Для неполярных жидкостей на низкоэнергетической поверхности твердого тела для работы адгезии было получено выражение

. (1.2.55)

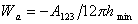
Поэтому уравнение Дюпре (1.2.46) можно записать

. (1.2.55′)

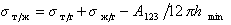
Для дисперсионной составляющей жидкости

, (1.2.56)

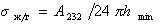
где А₂₃₂ – постоянная Гамакера взаимодействия жидкости через прослойку газа (пара).

Сочетая уравнения (1.2.47), (1.2.55) и (1.2.56), получаем

. (1.2.57)

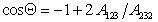
Очевидно, что Q = 0, т.е. при полном смачивании, cosQ = 1, если

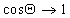
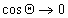
Уравнение (1.2.57) позволяет прогнозировать вероятность смачивания () или наоборот — несмачивания () жидкостью поверхности твердого тела по известным постоянным межмолекулярных сил взаимодействия.

Чаще, однако, прибегают к определению постоянной Гамакера по известному значению межфазового натяжения на границе «твердое тело — газ». Эту характеристику поверхности твердого тела находят при распространении подхода Джирифалько и Гуда, рассмотренного нами выше для границы двух жидкостей, на поверхность раздела «жидкость — твердое тело», уравнения (1.2.23), (1.2.35).

Так приложение уравнения (1.2.34) к уравнению Юнга для случая смачивания неполярной жидкостью поверхности полимерного материала позволяет получить уравнение, известное как уравнение Фоукса, при

. (1.2.58)

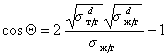
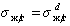
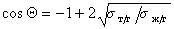
Если жидкости неполярны и , то уравнение (1.2.58) переходит в уравнение

. (1.2.59)

Уравнение (1.2.59) Зисман предложил использовать для определения поверхностного натяжения твердых тел. Очевидно, что при 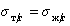cosQ =1, а угол смачивания будет равен нулю (Q = 0), т.е. наступает полное смачивание.

Естественно, что метод Зисмана ограничен некоторыми условиями, в частности, из уравнения (1.2.57) следует, что полное смачивание возможно при дисперсионной неразличимости твердого тела и жидкости, т.е. при А₂₃₂= А₁₂₃.

В действительности такого условия никогда невозможно достигнуть хотя бы потому, что если жидкость и твердое тело будут иметь одинаковый химический состав, их постоянные Гамакера будут различаться из-за различий в плотности.

Другое ограничение, связанное с применением метода Зисмана, основано на том, что использовать для измерения краевых углов смачивания следует лишь неполярные жидкости. Наиболее целесообразно применять гомологические ряды жидкостей. При величине поверхностного натяжения жидкостей более 35 мДж/м 2 метод Зисмана уже дает высокую погрешность, так как необходимо учитывать вклад полярных сил, которые в отличие от дисперсионной составляющей могут иметь и отрицательное значение. С другой стороны, приложение для смачивания твердых тел полярными жидкостями уравнения Ву (1.2.36) позволяет рассчитать полярную составляющую поверхностного натяжения жидкости, если для одной из неполярных жидкостей измерить краевой угол смачивания. Для расчета используют уравнение

Рис. 1.25. Зависимость смачивания поверхностей от поверхностного натяжения жидкостей. Материал поверхности: 1- FC-721; 2- ПТФЭ (тефлон); 3 — полиэтилен

. (1.2.60)

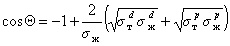
Этот метод позволил разделить величину поверхностного натяжения жидкостей на полярную и дисперсионную компоненты и определить поверхностное натяжение многих волокнообразующих полимеров.

Пример зависимости косинуса угла смачивания поверхности пленок различными жидкостями приведен на рис.1.25. Для описания этих зависимостей Зисман предложил использовать эмпирическое уравнение

, (1.2.61)

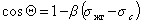
где bэмпирическая постоянная, s_с – «критическое» поверхностное натяжение твердого тела, при котором происходит полное смачивание твердого тела жидкостью. Очевидно, что cos Q =1 при условии s_жг = s_с .

Как мы обсуждали выше, этот критерий в известной мере является условным, хотя и отражает энергетическое состояние поверхности твердого тела.

Реальное значение поверхностного натяжения твердого тела экспериментально определить невозможно, также как и рассчитать его теоретически. В этой связи метод Зисмана нашел широкое применение в практике исследования полимерных материалов, а также полимерных покрытий тканей, используемых в качестве отделочных материалов