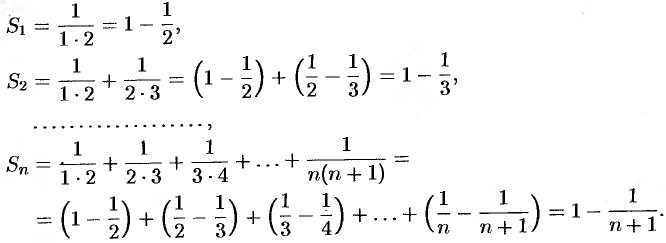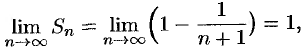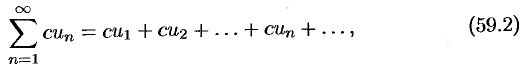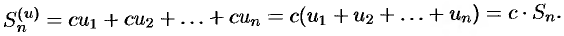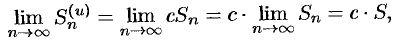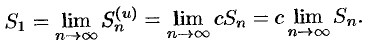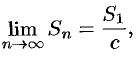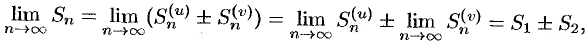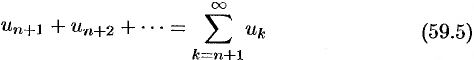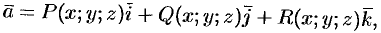На этой странице мы собрали простые и сложные примеры из курса высшей математики — от векторов и матриц до дифференциальных уравнений. На каждую тему приведен один решенный пример и даны ссылки на разделы, где собраны другие решения. Фактически, это шпаргалка-каталог типовых задач и решений к ним.
Если вам нужна помощь, узнайте больше о заказе решений по высшей математике.
- Далее решенные задачи по темам:
- Высшая математика. Комплексные числа
- Высшая математика. Матрицы
- Высшая математика. Определители
- Высшая математика. Системы уравнений
- Высшая математика. Векторы
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Высшая математика. Пределы
- Высшая математика. Производные
- Высшая математика. Исследование функции
- Высшая математика. Интегралы
- Высшая математика. Применение интегралов
- Высшая математика. Ряды
- Высшая математика. Дифференциальные уравнения
- Высшая математика. Теория вероятностей
- Математика
- Высшая математика — задачи с решением и примерами
- Высшая математика
- Элементы линейной алгебры
- Матрицы
- Определители
- Системы линейных уравнений
- Элементы векторной алгебры
- Векторы
- Аналитическая геометрия на плоскости
- Система координат на плоскости
- Преобразование системы координат
- Линии второго порядка на плоскости
- Аналитическая геометрия в пространстве
- Уравнения поверхности и линии в пространстве
- Канонические уравнения поверхностей второго порядка
- Введение в математический анализ
- Множество чисел
- Понятие функции
- Числовые функции. График функции. Способы задания функций
- Основные характеристики функции
- Предел функции
- Эквивалентные бесконечно малые функции
- Непрерывность функций
- Производная функции
- Задачи, приводящие к понятию производной
- Дифференцирование неявных и параметрически заданных функций
- Производные высших порядков
- Дифференциал функции
- Понятие дифференциала функции
- Геометрический смысл дифференциала функции
- Основные теоремы о дифференциалах
- Исследование функций при помощи производных
- Комплексные числа
- Понятие и представления комплексных чисел
- Неопределенный интеграл
- Понятие неопределенного интеграла
- Основные методы интегрирования
- Интегрирование рациональных функций
- Интегрирование тригонометрических функций
- Интегрирование иррациональных функций
- Определенный интеграл
- Несобственные интегралы
- Геометрические и физические приложения определенного интеграла
- Механические приложения определенного интеграла
- Приближенное вычисление определенного интеграла
- Функции нескольких переменных
- Производные и дифференциалы функции нескольких переменных
- Экстремум функции двух переменных
- Дифференциальные уравнения
- Общие сведения о дифференциальных уравнениях
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Линейные дифференциальные уравнения высших порядков
- Интегрирование дифференциальных уравнений второго порядка с постоянными коэффициентами
- Линейные неоднородные дифференциальные уравнения (лнду)
- Системы дифференциальных уравнений
- Двойные и тройные интегралы
- Двойной интеграл
- Геометрический и физический смысл двойного интеграла
- Основные свойства двойного интеграла
- Тройной интеграл
- Криволинейные и поверхностные интегралы
- Криволинейный интеграл I рода
- Криволинейный интеграл II рода
- Поверхностный интеграл I рода
- Поверхностный интеграл II рода
- Числовые ряды
- Знакочередующиеся и знакопеременные ряды
- Степенные ряды
- Разложение функций в степенные ряды
- Ряды Фурье. Интеграл Фурье
- Элементы теории поля
- Основные понятия теории поля
- Скалярное поле
- Векторное поле
Далее решенные задачи по темам:
Видео:Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать

Высшая математика. Комплексные числа
Задача. Вычислить сумму $(z_1 + z_2)$ и разность $(z_1 — z_2)$ комплексных чисел, заданных в показательной форме, переведя их в алгебраическую форму. Построить операнды и результаты на комплексной плоскости.
Видео:Самая сложная задача из самой сложной олимпиады [3Blue1Brown]Скачать
![Самая сложная задача из самой сложной олимпиады [3Blue1Brown]](https://i.ytimg.com/vi/S6_R5j8hzbY/0.jpg)
Высшая математика. Матрицы
Задача. Найти матрицу, обратную матрице $A$. Сделать проверку.
$$A= begin 1 & 2 & 1 & -1\ 1 & 1 & 0 & 0\ 0 & 2 & 0 & -1\ 1 & 1 & 1 & 0\ end $$
Видео:Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Высшая математика. Определители
Задача. Вычислить определитель матрицы $A$
$$A= begin 4 & 5 & 6 & 5 & 11\ 1 & 4 & 2 & 0 & 13\ 1 & 1 & 0 & -1 & 5\ 3 & 2 & 3 & 0 & 7\ 4 & 1 & 2 & 3 & 8\ end $$
Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Высшая математика. Системы уравнений
Задача. Исследовать на совместность и решить систему уравнений:
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Высшая математика. Векторы
Задача. Написать разложение вектора $X$ по векторам $(a, b, c)$.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Аналитическая геометрия на плоскости
Задача. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Видео:8 ЛОГИЧЕСКИХ ЗАГАДОК ДЛЯ САМЫХ УМНЫХ! Насколько хорошо развит твой мозг?Скачать

Аналитическая геометрия в пространстве
Задача. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.
Видео:Математика это не ИсламСкачать

Высшая математика. Пределы
Задача. Найти предел функции
Видео:9 Математических Загадок, Которые Поставят в Тупик Даже Самых УмныхСкачать

Высшая математика. Производные
Задача. Найти производную от следующей функции
Видео:Проверь свои знания по математике за 11 классСкачать

Высшая математика. Исследование функции
Задача. Провести полное исследование функции и построить график.
Видео:Считаем в уме за секунду. #математика #арифметика #счет #ментальнаяарифметика #simplemathСкачать

Высшая математика. Интегралы
Видео:Как умножать сложные числа? Лайфхак👌 #shortsСкачать

Высшая математика. Применение интегралов
Задача. Найти длину дуги кривой, заданной параметрическими уравнениями:
$$ x=3(1-cos t)cos t, quad y=3(1-cos t)sin t, quad 0leq t leq pi. $$
Высшая математика. Кратные и криволинейные интегралы
Видео:Мэри решает сложные примеры по математике | Одарённая (2017)Скачать

Высшая математика. Ряды
Задача. Исследовать сходимость числового ряда
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Высшая математика. Дифференциальные уравнения
Задача. Найти общее решение линейного дифференциального уравнения первого порядка
Видео:Высшая математика. Рисую дерево вышматаСкачать

Высшая математика. Теория вероятностей
Задача. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит 8; б) произведение числа очков не превосходит 8; в) произведение числа очков делится на 8.
Видео:Как использовать интеграл в обычной жизни. Математик МГУ и Савватеев #shortsСкачать

Математика
52. Более сложные примеры уравнений.
Пример 1 .
5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)
Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:
или, после сокращения,
5(x + 1) – 3(x – 1) = 15
5x + 5 – 3x + 3 = 15
Рассмотрим еще уравнение:
5/(x-1) – 3/(x+1) = 4(x 2 – 1)
Решая, как выше, получим:
5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.
Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.
Для первого примера получим:
Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.
Для второго примера получим:
5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0
Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.
Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.
(x + 3)/(x – 1) = (2x + 3)/(2x – 2)
Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:
(x + 3) (2x – 2) = (2x + 3) (x – 1)
2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.
Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:
6x – 2x – 6 = 3x – 2x – 3
Перенесем неизвестные члены влево, известные вправо — получим:
Вспоминая данное уравнение
(x + 3)/(x – 1) = (2x + 3)/(2x – 2)
мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.
Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:
2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,
Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:
(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)
Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:
Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:
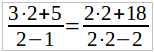
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:
(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.
Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы
Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:
1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2
Если мы вспомним начальное уравнение
(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),
то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.
Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:
1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),
2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),
3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).
Общий знаменатель равен (x – 3)(x – 2)(x + 1).
Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:
на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:
3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.
Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.
Если бы мы взяли уравнение:
то, поступая совершенно так же, как выше, получили бы
3(x + 1) – 2(x – 3) = x – 2
3x + 3 – 2x + 6 = x – 2
3x – 2x – x = –3 – 6 – 2,
откуда получили бы
что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.
Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Высшая математика — задачи с решением и примерами
Прежде чем изучать готовые решения задач по высшей математике, нужно знать теорию, поэтому для вас я подготовила лекции по предмету «высшая математика», в которых подробно решены задачи.
Я собрала весь курс лекций с примерами решения по всем разделам высшей математики, это самый полный курс лекций на сегодняшний день в интернете! Он подходит для школьников и студентов всех курсов и специальностей обучения. Курс лекций содержит, правила, теоремы, примеры решения.
Эта страница подготовлена для школьников и студентов.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Видео:Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Высшая математика
Высшая математика — это совокупность математических дисциплин, преподаваемых в высших учебных заведениях (ВУЗах). В разных университетах могут преподаваться разные наборы математических дисциплин.
В технических университетах и институтах, например, курс высшей математики может включать следующие разделы:
- аналитическая геометрия и линейная алгебра;
- математический анализ в объёме дифференцирования и интегрирования функции одной переменной и функции нескольких переменных;
- теория кратных интегралов и векторное поле;
- обыкновенные дифференциальные уравнения;
- числовые и функциональные ряды;
- теория функции комплексного переменного;
- преобразование Лапласа и операционное исчисление;
- гармонический анализ и теория рядов Фурье;
- уравнения математической физики; вариационное исчисление.
В высших учебных заведениях с гуманитарной и экономической направленностью курс по высшей математике может существенно отличаться от соответствующего курса в техническом университете. Скорее всего, экономисты и гуманитарии изучают только основы линейной алгебры и математического анализа.
Во многих высших учебных заведениях курс высшей математики включает такие разделы, как дискретная математика: математическая логика; теория графов и др.
Высшая математика считается самым сложным предметом в университете.
Видео:Профильный ЕГЭ 2022. Сложные уравнения. Задание 12Скачать

Элементы линейной алгебры
Линейная алгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения[⇨], системы линейных уравнений[⇨], среди основных инструментов, используемых в линейной алгебре — определители, матрицы[⇨], сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры. Такие объекты как квадратичные и билинейные формы[⇨], тензоры[⇨] и операции как тензорное произведение непосредственно вытекают из изучения линейных пространств, но как таковые относятся к полилинейной алгебре.
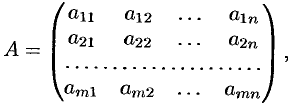
Матрицы
Основные понятия
Матрицей называется прямоугольная таблица чисел, содержащая 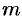
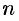
или, сокращенно, 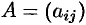
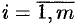
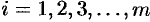
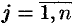
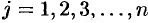
Матрицу 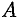
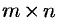
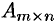
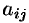
Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е.
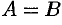

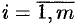
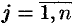
Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера 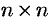
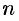
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой 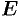
Пример №1.1.
— единичная матрица 3-го порядка.
— единичная матрица 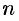
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой 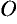
В матричном исчислении матрицы 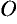
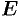
Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:
Матрица размера 
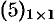
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается 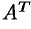
Так, если 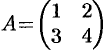
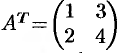
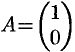
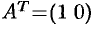
Транспонированная матрица обладает следующим свойством: 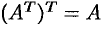
Лекции и примеры решения к этой теме:
Определители
Основные понятия
Квадратной матрице 
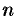
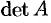
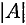

Определитель матрицы 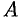
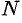
Вычисление определителя 2-го порядка иллюстрируется схемой:
Пример №2.1.
Найти определители матриц
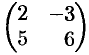
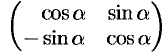
Решение:
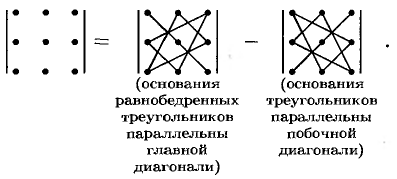
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:
Лекции и примеры решения к этой теме:
Системы линейных уравнений
Основные понятия
Системой линейных, алгебраических уравнений, содержащей 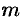
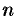
где числа 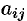
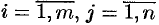
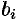
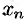
Такую систему удобно записывать в компактной матричной
форме
Здесь 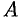
матрицей:
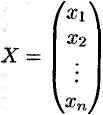
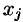
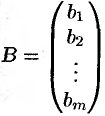
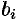
Произведение матриц 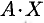
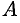
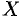
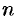
Расширенной матрицей системы называется матрица 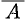
Решением системы называется 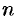
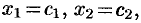
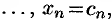
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется оборш решением.
Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Две; системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
Однородная система всегда совместна, так как 
Лекции и примеры решения к этой теме:
Элементы векторной алгебры
Векторная алгебра — это раздел математики, отвечающий за изучение систем линейных уравнений, векторов, матриц, векторных пространств и их линейных преобразований.
Векторная алгебра в высшей математике распределена по разделам:
- раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства;
- часть линейной алгебры, занимающаяся векторными пространствами;
- различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы
Основные понятия
Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.
Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.
Вектор — это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если 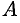
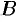
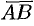

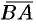
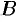
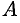
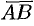


Длиной или модулем вектора 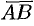
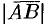
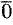
Вектор, длина которого равна единице, называется единичным вектором и обозначается через 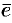


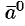
Векторы 

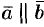
Коллинеарные векторы могут быть направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным любому вектору.
Два вектора 

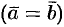
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку 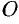
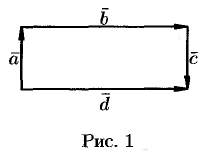
На рисунке 1 векторы образуют прямоугольник. Справедливо равенство 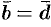
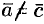

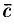
Равные векторы называют также свободными.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хота бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
Лекции и примеры решения к этой теме:
Аналитическая геометрия на плоскости
Аналитическая геометрия — раздел геометрии, в котором геометрические фигуры и их свойства исследуются средствами алгебры. В основе этого метода лежит так называемый метод координат, впервые применённый Декартом в 1637 году. Каждому геометрическому соотношению этот метод ставит в соответствие некоторое уравнение, связывающее координаты фигуры или тела. Такой метод «алгебраизации» геометрических свойств доказал свою универсальность и плодотворно применяется во многих естественных науках и в технике.
В высшей математике аналитическая геометрия является также основой для других разделов геометрии — например, дифференциальной, алгебраической, комбинаторной и вычислительной геометрии.
Система координат на плоскости
Основные понятия
Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Одной
из таких систем является прямоугольная (декартова) система координат.
Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми — осями, на каждой из которых выбрано положительное направление и задан единичный (масштабный) отрезок. Единицу масштаба обычно берут одинаковой для обеих осей. Эти оси называют осями координат, точку их пересечения 
На рисунках ось абсцисс, обычно располагают горизонтально и направленной слева направо, а ось ординат — вертикально и направленной снизу вверх. Оси координат делят плоскость на четыре области — четверти (или квадранты).
Единичные векторы осей обозначают 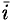
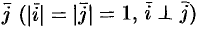
Систему координат обозначают 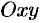
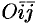
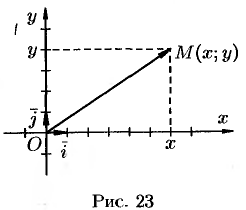
Рассмотрим произвольную точку 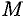
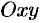
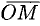
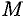
Координатами точки 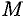
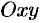
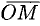
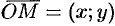
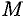
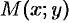
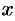
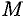
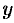
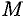
Эти два числа 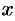
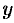
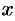
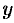
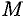
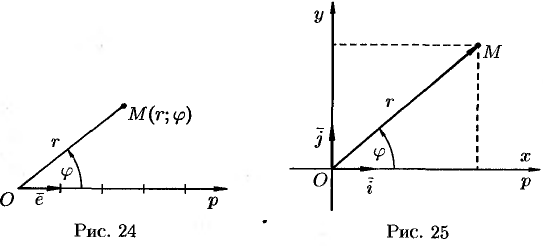
Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой 
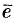
Возьмем на плоскости точку 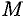
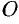
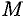
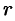
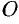
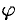
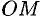
Числа 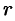
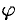
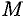
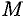
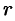
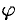
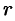
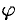
Для получения всех точек плоскости достаточно полярный угол 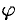
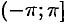
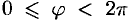
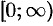
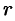
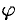
Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс 
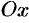
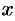
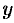
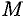
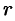
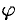
Из рисунка 25 видно, что прямоугольные координаты точки 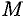
Полярные же координаты точки 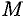
Определяя величину 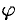
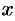
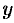
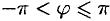
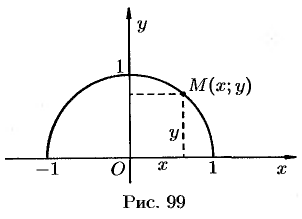
Пример №9.1.
Дана точка 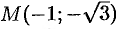
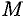
Решение:
Находим 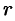
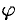
Отсюда 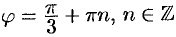
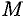
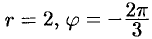
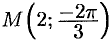
Лекции и примеры решения к этой теме:
Преобразование системы координат
Основные понятия
Переход от одной системы координат в какую-либо другую называется преобразованием системы, координат.
Рассмотрим два случая преобразования одной прямоугольной системы координат в другую. Полученные формулы устанавливают зависимость между координатами произвольной точки плоскости в разных системах координат.
Лекции и примеры решения к этой теме:
Линии второго порядка на плоскости
Основные понятия
Рассмотрим .пинии, определяемые уравнениями второй степени относительно текущих координат
Коэффициенты уравнения — действительные числа, но по крайней мере одно из чисел 
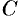
Лекции и примеры решения к этой теме:
Аналитическая геометрия в пространстве
Аналитическая геометрия — раздел геометрии, в котором с помощью алгебры исследуются геометрические фигуры и их свойства. Этот метод основан на так называемом координатном методе, впервые примененном Декартом в 1637 году. Каждому геометрическому соотношению этот метод ставит в соответствие некоторое уравнение, связывающее координаты фигуры или тела. Этот метод «алгебры» геометрических свойств доказал свою многогранность и плодотворно применяется во многих естественных науках и техниках.
Уравнения поверхности и линии в пространстве
Лекции и примеры решения к этой теме:
Канонические уравнения поверхностей второго порядка
По заданному уравнению поверхности второго порядка (т. е. поверхности, уравнение которой в прямоугольной системе координат является алгебраическим уравнением второй степени) будем определять ее геометрический вид. Для этого применим так называемый метод сечений: исследование вида поверхности будем производить при помощи изучения линий пересечения данной поверхности с координатными плоскостями или плоскостями, им параллельными.
Лекции и примеры решения к этой теме:
Введение в математический анализ
Математический анализ — это совокупность разделов математики, соответствующих историческому разделу под наименованием «анализ бесконечно малых», объединяет дифференциальное[⇨] и интегральное[⇨] исчисления.
Множество чисел
Лекции и примеры решения к этой теме:
Понятие функции
Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи) между элементами двух множеств.
Пусть даны два непустых множества 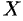
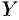
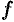
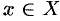
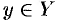

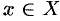
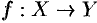
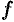
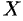
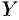
Например, соответствия 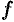
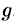
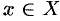
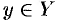
Множество 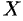
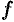
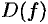
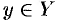
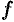
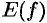
Числовые функции. График функции. Способы задания функций
Пусть задана функция 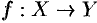
Если элементами множеств 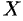
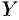
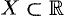
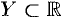
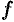

Переменная 
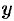


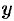
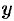

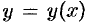
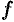
Частное значение функции 
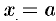
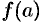
Например, если 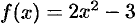
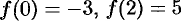
Графиком функции 

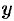
Например, графиком функции 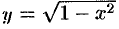
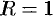
Чтобы задать функцию 

Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.
Аналитический способ: функция задается в виде одной или нескольких формул или уравнений.
Если область определения функции 
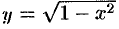
Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию 
Графический способ: задается график функции.
Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Значения функции 

Преимуществом графического задания является его наглядность, недостатком — его неточность.
Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы.
На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений.
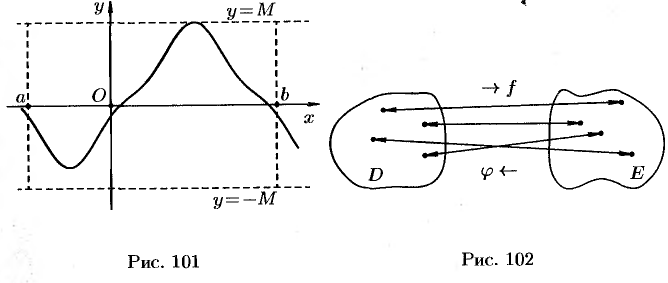
Основные характеристики функции
1. Функция 
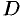
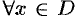
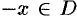
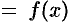
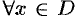
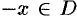
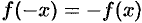
График четной функции симметричен относительно оси 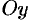
Например, 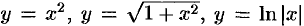
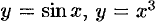
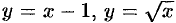
2. Пусть функция 
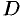
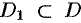
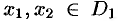
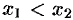
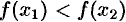
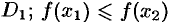
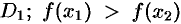
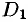
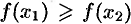
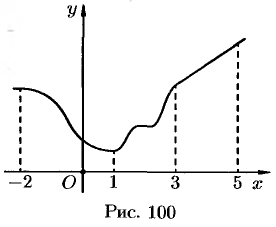
Например, функция, заданная графиком (см. рис. 100), убывает на интервале (—2; 1), не убывает на интервале (1; 5), возрастает на интервале (3; 5).
Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве 
3. Функцию 
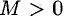
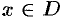
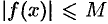
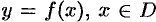
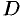
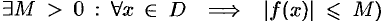
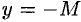
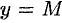
4. Функция 
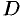
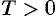
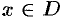
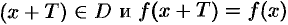
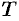
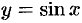
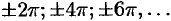
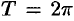
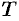
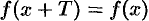
Лекции и примеры решения к этой теме:
Предел функции
Предел функции в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке. Одно из основных понятий математического анализа.
Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, являющихся образами точек такой последовательности элементов области определения функции, которая сходится к точке, в которой рассматривается предел. Если такой предел существует, то говорят, что функция сходится к указанному значению, иначе говорят, что функция расходится.
Лекция и примеры решения к этой теме:
Эквивалентные бесконечно малые функции
Быстрым способом нахождения пределов функций имеющих особенности вида ноль на ноль является применение эквивалентных бесконечно малых функций. Они крайне необходимы если нужно находить границы без применения правила Лопиталя. Эквивалентности заключаются в замене функции ее разложением в ряд Маклорена. Как правило при вычислении предела используют не более двух членов разложения.
Лекция и примеры решения к этой теме:
Непрерывность функций
Непрерывная функция — это функция, которая меняется без мгновенных «скачков» (называемых разрывами), то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции. График непрерывной функции является непрерывной линией.
Лекции и примеры решения к этой теме:
Производная функции
Производная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференцированием. Обратный процесс — нахождение первообразной — интегрирование.
Задачи, приводящие к понятию производной
Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости разных процессов.
Лекции и примеры решения к этой теме:
Дифференцирование неявных и параметрически заданных функций
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Лекции и примеры решения к этой теме:
Производные высших порядков
Если функция y=f(x) имеет производную в каждой точке x своей области определения, то ее производная f′(x) есть функция от x. Функция y=f′(x), в свою очередь, может иметь производную, которую называют производной второго (высшего) порядка функции y=f(x) (или второй производной) и обозначают символом f′′(x).
Лекции и примеры решения к этой теме:
Дифференциал функции
Дифференциал — это линейная часть приращения функции.
Понятие дифференциала функции
Пусть функция 

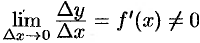
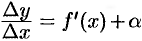
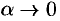
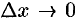
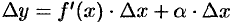
Таким образом, приращение функции 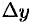
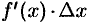
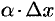
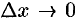
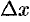
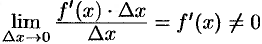
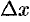
Поэтому первое слагаемое 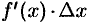
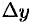
Дифференциалом функции 

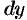
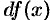
Дифференциал 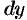


Так как 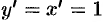
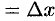
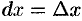
Поэтому формулу (24.1) можно записать так:
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (24.2) следует равенство 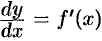
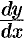
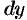
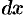
Пример №24.1.
Найти дифференциал функции
Решение:
По формуле 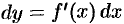
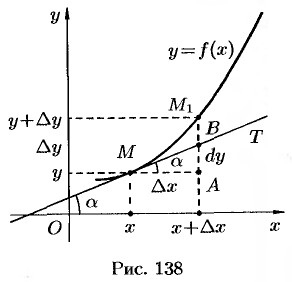
Геометрический смысл дифференциала функции
Выясним геометрический смысл дифференциала.
Для этого проведем к графику функции 
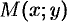
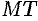
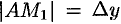
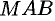
Но, согласно геометрическому смыслу производной, 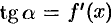
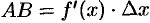
Сравнивая полученный результат с формулой (24.1), получаем 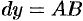



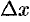
В этом и состоит геометрический смысл дифференциала.
Основные теоремы о дифференциалах
Основные теоремы о дифференциалах легко получить, используя связь дифференциала и производной функции 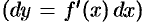
Например, так как производная функции 
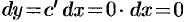
Теорема 24.1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:
Докажем, например, вторую формулу. По определению дифференциала имеем:
Теорема 24.2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Пусть 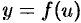
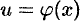
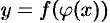
Умножив обе части этого равенства на 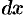
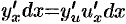
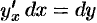
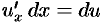
Сравнивая формулы 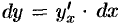
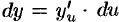

Это свойство дифференциала называют инвариантностью (неизменностью) формы первого дифференциала.
Формула 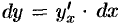
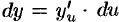

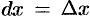

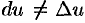
С помощью определения дифференциала и основных теорем о дифференциалах легко преобразовать таблицу производных в таблицу дифференциалов.
Например, 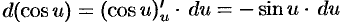
Лекции и примеры решения к этой теме:
Исследование функций при помощи производных
В заданиях ЕГЭ по математике обязательно встретиться исследование функции с помощью производной. Исследование функций при помощи производных – не самая простая в мире вещь. Но в КИМах не встречается такого, с чем бы не справился ученик средней школы, если он приложил достаточно стараний к учебе.
Лекции и примеры решения к этой теме:
Комплексные числа
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.
Понятие и представления комплексных чисел
Основные понятия
Комплексным числом 
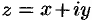


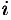

Если 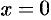
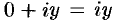
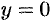
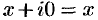

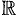
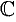
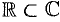
Число 
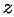
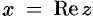

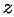
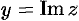
Два комплексных числа 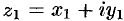
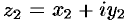
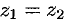
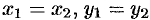
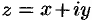
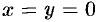
Два комплексных числа 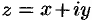
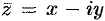
Лекции и примеры решения к этой теме:
Неопределенный интеграл
Неопределённый интеграл для функции f(x) — это совокупность всех первообразных данной функции.
Понятие неопределенного интеграла
В дифференциальном исчислении решается задача: по данной функции 
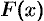
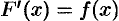
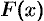

Функция 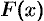

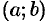
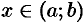
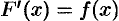
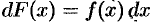
Например, первообразной функции 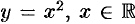
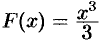
Очевидно, что.первообразными будут также любые функции
где 
Теорема 29.1. Если функция 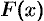

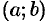

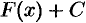
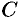
Функция 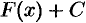

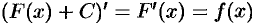
Пусть 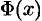
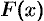

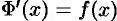
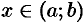
А это означает (см. следствие 25.1), что
где 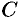
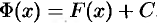
Множество всех первообразных функций 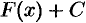


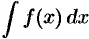
Таким образом, по определению
Здесь 
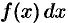


Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
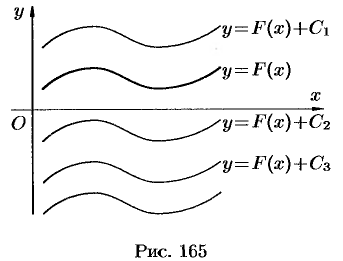
Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых 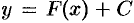
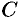
Для всякой ли функции существует неопределенный интеграл?
Имеет место теорема, утверждающая, что «всякая непрерывная на 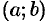
Лекции и примеры решения к этой теме:
Основные методы интегрирования
Лекции и примеры решения к этой теме:
Интегрирование рациональных функций
Лекции к этой теме:
Интегрирование тригонометрических функций
Лекции и примеры решения к этой теме:
Интегрирование иррациональных функций
Лекции и примеры решения к этой теме:
Определенный интеграл
Определённый интеграл — одно из основных понятий математического анализа, один из видов интеграла. Определённый интеграл является числом, равным пределу сумм особого вида (интегральных сумм)[⇨]. Геометрически определённый интеграл выражает площадь «криволинейной трапеции», ограниченной графиком функции[⇨]. В терминах функционального анализа, определённый интеграл — аддитивный монотонный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).
Лекции и примеры решения к этой теме:
Несобственные интегралы
Определенный интеграл 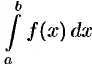



Рассмотрим так называемые несобственные интегралы, т. е. определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв.
Лекции и примеры решения к этой теме:
Геометрические и физические приложения определенного интеграла
Лекции и примеры решения к этой теме:
Механические приложения определенного интеграла
Лекции и примеры решения к этой теме:
Приближенное вычисление определенного интеграла
Лекция и примеры решения к этой теме:
Функции нескольких переменных
Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных.
Будем рассматривать функции двух переменных, так как все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных. Эти факты обобщаются на случай большего числа переменных. Кроме того, для функций двух переменных можно дать наглядную геометрическую интерпретацию.
Лекции и примеры решения к этой теме:
Производные и дифференциалы функции нескольких переменных
Лекции и примеры решения к этой теме:
Экстремум функции двух переменных
Основные понятия
Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной (см. п. 25.4).
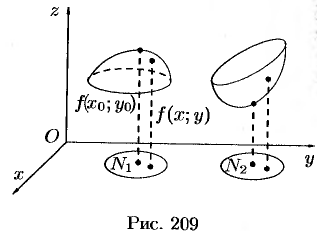
Пусть функция 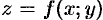
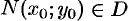
Точка 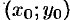
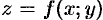
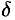
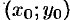
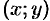
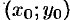
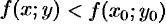
Аналогично определяется точка минимума функции: для всех точек 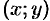
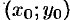
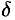
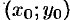
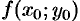
На рисунке 209: 
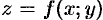
Значение функции в точке максимума (минимума) называется
максимумом (минимумом) функции. Максимум и минимум функции называют ее экстремумами.
Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке 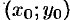
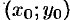
Лекции и примеры решения к этой теме:
Дифференциальные уравнения
Дифференциальное уравнение — уравнение, в которое входят производные функции и могут входить сама функция, независимая переменная и параметры. Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или могут отсутствовать вовсе, кроме хотя бы одной производной. Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением.
Общие сведения о дифференциальных уравнениях
Основные понятия
При решении различных задач математики, физики, химии и других наук часто пользуются математическими моделями в виде уравнений, связывающих независимую переменную, искомую функцию и ее производные. Такие уравнения называются дифференциальными (термин принадлежит Г. Лейбницу, 1676 г.). Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Так, решением уравнения 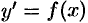

Рассмотрим некоторые общие сведения о дифференциальных уравнениях (ДУ).
Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называют обыкновенным; в противном случае — ДУ в частных производных. Далее будем рассматривать только обыкновенные ДУ.
Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения.
Например, уравнение 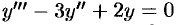

Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ — интегральной кривой.
Рассмотрим некоторые задачи, решение которых приводит к дифференциальным уравнениям.
Лекция и примеры решения к этой теме:
Дифференциальные уравнения первого порядка
Основные понятия
Дифференциальное уравнение первого порядка в общем случае можно записать в виде
Уравнение связывает независимую переменную 

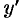
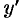
и называют ДУ первого порядка, разрешенным относительно производной. Мы в основном будем рассматривать эту форму записи ДУ.
Уравнение (48.2) устанавливает связь (зависимость) между координатами точки 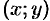
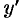
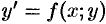
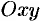
Кривая, во всех точках которой направление поля одинаково, называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить 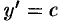
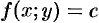
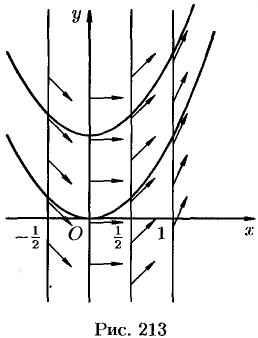
Пример №48.1.
С помощью изоклин начертить вид интегральных кривых уравнения 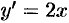
Решение:
Уравнение изоклин этого ДУ будет 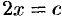
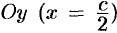

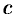
Так, при 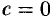
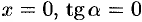
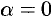
при 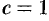
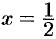
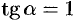
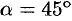
при 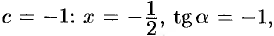
при 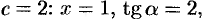
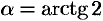
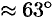
Построив четыре изоклины и отметив на каждой из них ряд стрелочек, наклоненных к оси 
Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:
где 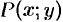
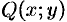


Интегрирование ДУ в общем случае приводит к бесконечному множеству решений (отличающихся друг от друга постоянными величинами). Легко догадаться, что решением уравнения 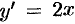
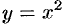
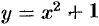
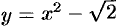
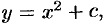
Чтобы решение ДУ приобрело конкретный смысл, его надо подчинить некоторым дополнительным условиям.
Условие, что при 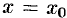

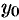

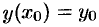
Общим решением ДУ первого порядка называется функция 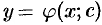
- Функция
является решением ДУ при каждом фиксированном значении
.
- Каково бы ни было начальное условие (48.4), можно найти такое значение постоянной
, что функция
удовлетворяет данному начальному условию.
Частным решением ДУ первого порядка называется любая функция 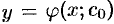
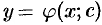
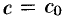
Если общее решение ДУ найдено в неявном виде, т. е. в виде уравнения 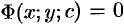
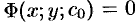
С геометрической точки зрения 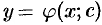
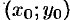
Задача отыскания решения ДУ первого порядка (48.3), удовлетворяющего заданному начальному условию (48.4), называется задачей Коши.
Теорема 48.1 (существования и единственности решения задачи Коши). Если в уравнении (48.2) функция 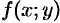
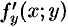
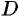
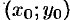
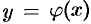
Геометрический смысл теоремы состоит в том, что при выполнении ее условий существует единственная интегральная кривая ДУ, проходящая через точку 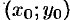
Рассмотрим теперь методы интегрирования ДУ первого порядка определенного типа.
Лекции и примеры решения к этой теме:
Дифференциальные уравнения высших порядков
Основные понятия
Дифференциальные уравнения порядка выше первого называются ДУ высших порядков. ДУ второго порядка в общем случае записывается в виде
или, если это возможно, в виде, разрешенном относительно старшей производной:
Будем в основном рассматривать уравнение вида (49.2): от него всегда, можно перейти к (49.1).
Решением ДУ (49.2) называется всякая функция 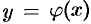
Общим решением ДУ (49.2) называется функция 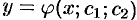
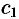
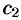

1. 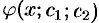
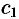
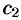
2. Каковы бы ни были начальные условия
существуют единственные значения постоянных 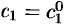
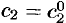
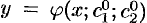
Всякое решение 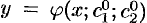
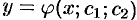
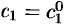
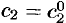
Решения ДУ (49.2), записанные в виде
называются общим и частным интегралом соответственно.
График всякого решения ДУ второго порядка называется интегральной кривой. Общее решение ДУ (49.2) представляет собой множество интегральных кривых; частное решение — одна интегральная кривая этого множества, проходящая через точку 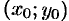
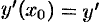
Переписав ДУ (49.1) в виде
видим, что ДУ второго порядка устанавливает связь между координатами точки 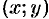
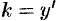
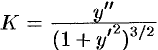
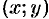
Как и в случае уравнения первого порядка, задача нахождения решения ДУ (49.2), удовлетворяющего заданным начальным условиям (49.3), называется задачей Коши.
Теорема 49.1 (существования и единственности задачи Коши). Если в уравнении (49.2) функция 
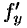
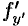
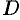


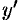
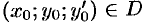
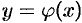
Примем теорему без доказательства.
Аналогичные понятия и определения имеют место для ДУ 
если его можно разрешить относительно старшей производной.
Начальные условия для ДУ (49.4) имеют вид
Общее решение ДУ 
содержащей 

Решение ДУ (49.4), получающееся из общего решения при конкретных значениях постоянных 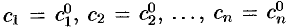
Задача Коши для ДУ 
Проинтегрировать (решить) ДУ 
Задача нахождения решения ДУ 
Лекция и примеры решения к этой теме:
Линейные дифференциальные уравнения высших порядков
Основные понятия
Многие задачи математики, механики, электротехники и других технических наук приводят к линейным дифференциальным уравнениям.
где 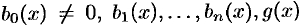


Оно содержит искомую функцию 
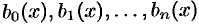
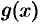
Если свободный член 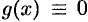
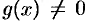
Разделив уравнение (49.11) на 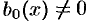
запишем уравнение (49.11) в виде приведенного:
Далее будем рассматривать линейные ДУ вида (49.12) и считать, что коэффициенты и свободный член уравнения (49.12) являются непрерывными функциями (на некотором интервале 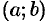
Лекции и примеры решения к этой теме:
Интегрирование дифференциальных уравнений второго порядка с постоянными коэффициентами
Лекции и примеры решения к этой теме:
Линейные неоднородные дифференциальные уравнения (лнду)
Лекции и примеры решения к этой теме:
Системы дифференциальных уравнений
Основные понятия
Для решения многих задач математики, физики, техники (задач динамики криволинейного движения; задач электротехники для нескольких электрических цепей; определения состава системы, в которой протекают несколько последовательных химических реакций I порядка; отыскания векторных линий ноля и других) нередко требуется несколько функций. Нахождение этих функций может привести к нескольким ДУ, образующим систему.
Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную, искомые функции и их производные.
Общий вид системы ДУ первого порядка, содержащей 
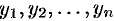
Система ДУ первого порядка, разрешенных относительно производной, т. е. система вида
называется нормальной системой ДУ. При этом предполагается, что число уравнений равно числу искомых функций.
Замечание. Во многих случаях системы уравнений и уравнения высших порядков можно привести к нормальной системе вида (52.1).
Так, система трех ДУ второго порядка
описывающая движение тонки в пространстве, путем введения новых переменных: 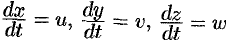
Уравнение третьего порядка 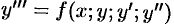
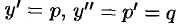
Из сказанного выше следует полезность изучения именно нормальных систем.
Решением системы (52.1) называется совокупность из 
системы.
Начальные условия для системы (52.1) имеют вид
Задача Коши для системы (52.1) ставится следующим образом: найти решение системы (52.1), удовлетворяющее начальным условиям (52.2).
Условия существования и единственности решения задачи Коши описывает следующая теорема, приводимая здесь без доказательства.
Теорема 52.1 (Коши). Если в системе (52.1) все функции
непрерывны вместе со всеми своими частными производными по 

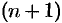
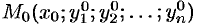
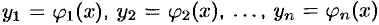
Меняя в области 
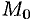

Это решение является общим, если по заданным начальным условиям (52.2) можно однозначно определить постоянные 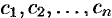
Решение, получающееся из общего при конкретных значениях постоянных 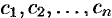
Лекции и примеры решения к этой теме:
Двойные и тройные интегралы
Двойной интеграл — это обобщение понятия определенного интеграла на двумерный случай.
Тройной интеграл — это аналог двойного интеграла для функции трёх переменных, заданной как f(M) = f(x, y, z).
Двойной интеграл
Основные понятия и определения
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
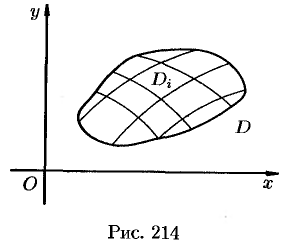
Пусть в замкнутой области 
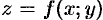

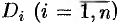
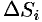
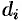
В каждой области 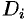
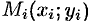
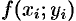
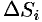
(53.1) Эта сумма называется интегральной суммой функции 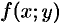

Рассмотрим предел интегральной суммы (53.1), когда 
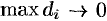

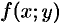

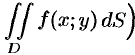
Таким образом, двойной интеграл определяется равенством
В этом случае функция 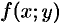




Для всякой ли функции 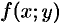
Теорема 53.1 (достаточное условие интегрируемости функции). Если функция 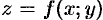

- Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
- Из определения двойного интеграла следует, что для интегрируемой в области
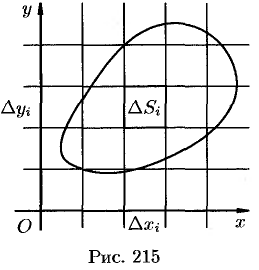
функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область
на площадки
прямыми, параллельными координатным осям (см. рис. 215). При этом, равенство (53.2) можно записать в виде
Геометрический и физический смысл двойного интеграла
Рассмотрим две задачи, приводящие к двойному интегралу, по ссылкам:
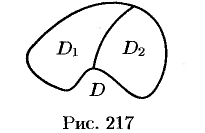
Основные свойства двойного интеграла
Можно заметить, что процесс построения интеграла в области 

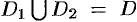
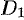
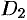
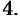

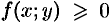
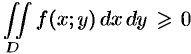

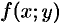
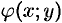
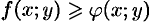
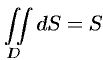
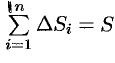
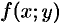


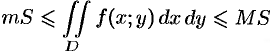
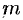


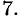
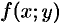


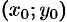
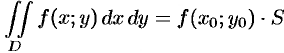
называют средним значением функции 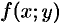

Лекции и примеры решения к этой теме:
Тройной интеграл
Основные понятия
Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».
Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.
Пусть в замкнутой области 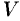
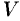

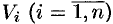
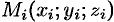
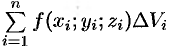
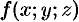
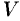
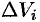
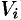
Если предел интегральной суммы существует при неограниченном увеличении числа 
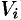
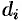
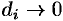
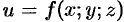

Таким образом, по определению, имеем:
Здесь 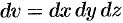
Теорема 54.1 (существования). Если функция 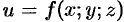
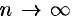
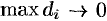
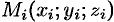
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:
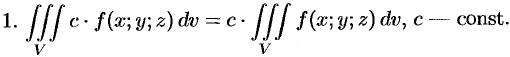
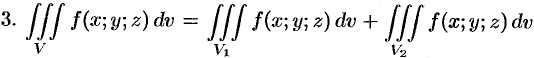
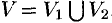
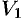
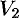
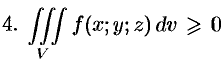

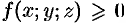
Если в области интегрирования 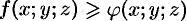
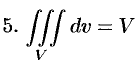
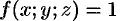
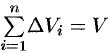
где 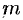

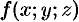

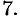
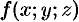

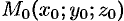
где 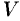
Лекции и примеры решения к этой теме:
Криволинейные и поверхностные интегралы
Обобщением определенного интеграла на случай, когда область интегрирования есть некоторая кривая, является так называемый криво линейный интеграл.
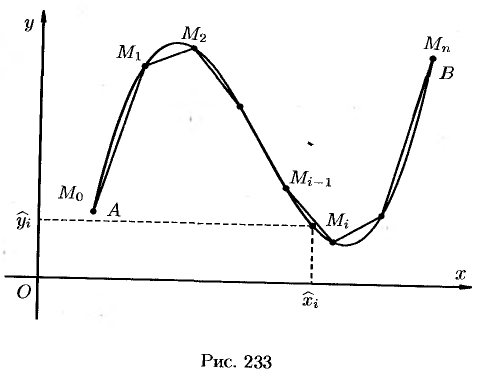
Криволинейный интеграл I рода
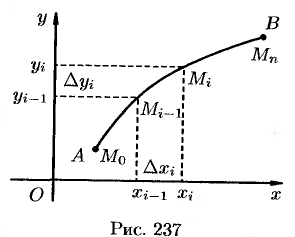
Основные понятия
Пусть на плоскости 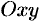


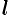
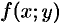


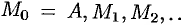
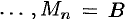

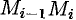
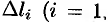

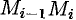
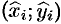

Ее называют интегральной суммой, для функции 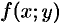

Пусть 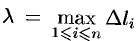
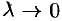
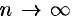
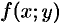

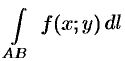
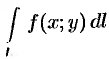
Таким образом, по определению,
Условие существования криволинейного интеграла 1 рода (существования предела интегральной суммы (55.1) при 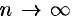
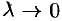
Теорема 55.1. Если функция 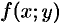
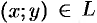
Аналогичным образом вводится понятие криволинейного интеграла от функции 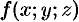

Приведем основные свойства криволинейного интеграла по длине дуги (I рода).
1. 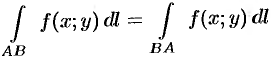
2.
3.
4. 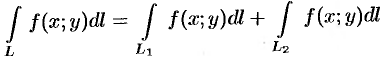

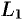
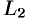
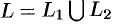
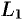
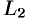
5. Если для точек кривой 
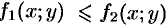
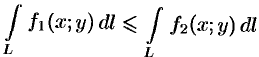
6. 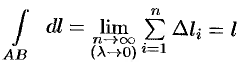
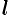

7. Если функция 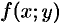

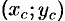
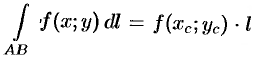
Лекции и примеры решения к этой теме:
Криволинейный интеграл II рода
Основные понятия
Решение задачи о вычислении работы переменной силы при перемещении материальной точки вдоль некоторой кривой (и других) приводит к понятию криволинейного интеграла II рода.
Криволинейный интеграл II рода определяется почти так же, как и интеграл I рода.
Пусть в плоскости 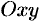


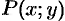

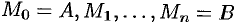

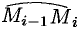
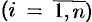
На каждой «элементарной дуге» 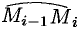
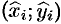
где 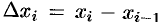
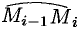

Сумму (56.1) называют интегральной суммой для функции 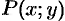

Если при 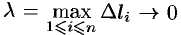

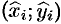

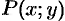

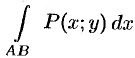
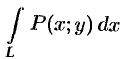
Аналогично вводится криволинейный интеграл от функции 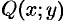

где 
Криволинейный интеграл II рода общего вида
Криволинейный интеграл 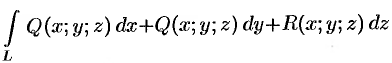

Теорема 56.1. Если кривая 

Отметим лишь некоторые свойства криволинейного интеграла II рода.
1. При изменении направления пути интегрирования криволинейный интеграл II рода изменяет свой знак на противоположный, т. е.
(проекция дуги 

2. Если кривая 
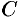
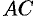
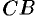
3. Если кривая 

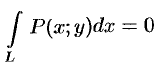
аналогично для кривой, лежащей в плоскости, перпендикулярной оси 
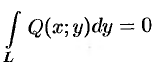
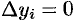
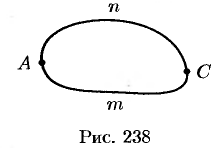
4. Криволинейный интеграл по замкнутой кривой (обозначается 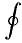
(см. рис. 238). С другой стороны,
Лекции и примеры решения к этой теме:
Поверхностный интеграл I рода
Основные понятия
Обобщением двойного интеграла является так называемый поверхностный интеграл.
Пусть в точках некоторой поверхности 

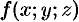


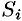
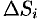
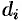
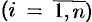
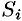
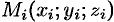
Она называется интегральной для функции 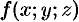

Если при 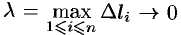
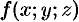

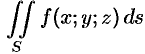
Таким образом, по определению,
Отметим, что «если поверхность 
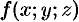
Поверхностный интеграл I рода обладает следующими свойствами:
1. 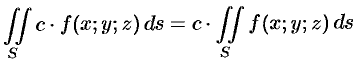
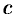
2.
3. Если поверхность 
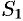
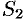
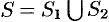
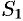
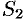
4. Если на поверхности 
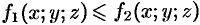
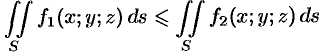
5. 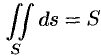


6. 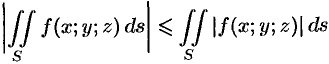
7. Если 

(теорема о среднем значении).
Лекции и примеры решения к этой теме:
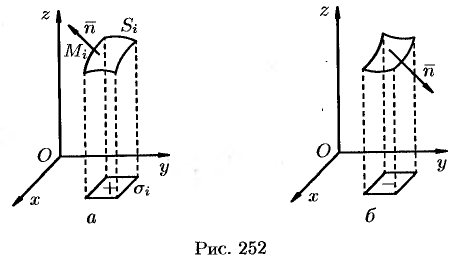
Поверхностный интеграл II рода
Основные понятия
Поверхностный интеграл II рода строится по образцу криволинейного интеграла II рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет.
Пусть задана двусторонняя поверхность (таковой является плоскость, эллипсоид, любая поверхность, задаваемая уравнением 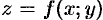
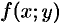
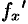
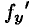

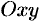
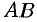
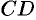
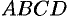
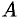
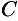


Далее, пусть в точках рассматриваемой двусторонней поверхности 
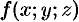
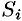
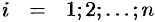
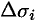
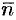
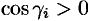
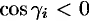
где 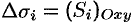
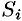
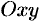
Предел интегральной суммы (58.1) при 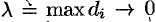

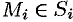
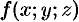


Аналогично определяются поверхностные интегралы II рода по переменным 



Общим видом поверхностного интеграла II рода служит интеграл
где 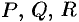

Отметим, что если 
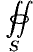
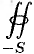
Из определения поверхностного интеграла II рода вытекают следующие его свойства:
- Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.
- Постоянный множитель можно выносить за знак поверхностного интеграла.
- Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
- Поверхностный интеграл II рода по всей поверхности
равен сумме интегралов по ее частям
и
(аддитивное свойство), если
и
пересекаются лишь по границе, их разделяющей.
- Если
— цилиндрические поверхности с образующими, параллельными соответственно осям
, то
Лекции и примеры решения к этой теме:
Числовые ряды
Основные понятия
Бесконечные ряды широко используются в теоретических исследованиях математического анализа, имеют разнообразные практические применения.
Числовым рядом (или просто рядом) называется выражение вида
где 
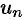
Ряд (59.1) считается заданным, если известен общий член рада 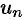
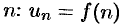
Сумма первых 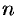
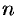
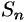
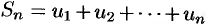
Рассмотрим частичные суммы
Если существует конечный предел 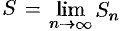
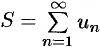
Если 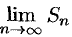
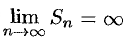
- Ряд
нельзя считать заданным, а ряд 2 + 5 + 8 +… — можно: его общий член задастся формулой
.
- Ряд 0 + 0 + 0 + … + 0 + … сходится, его сумма равна 0.
- Ряд 1 + 1 + 1 + … + 1 + … расходится,
при
.
- Ряд 1—1+1—1+1—1+… расходится, так как последовательность частичных сумм 1,0,1,0,1,0,…
не имеет предела.
- Ряд
сходится. Действительно,
т. e. ряд сходится, его сумма равна 1.
Рассмотрим некоторые важные свойства рядов.
Свойство 1. Если ряд (59.1) сходится и его сумма равна 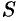
где 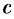
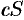
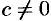
Обозначим 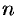
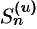
т.е. ряд (59.2) сходится и имеет сумму 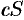
Покажем теперь, что если ряд (59.1) расходится, 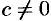
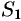
т. e. ряд (59.1) сходится, что противоречит условию о расходимости ряда (59.1).
Свойство 2. Если сходится ряд (59.1) и сходится ряд
а их суммы равны 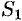
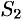
причем сумма каждого равна соответственно 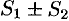
Обозначим 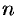
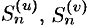
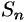
т. e. каждый из рядов (59.4) сходится, и сумма его равна 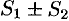
Из свойства 2 вытекает, что сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд.
В справедливости этого утверждения можно убедиться методом от противного.
Заметим, что сумма (разность) двух расходящихся рядов может быть как сходящимся, так и расходящимся рядом.
Свойство 3. Если к ряду (59.1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (59.1) сходятся или расходятся одновременно.
Обозначим через 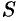
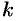
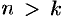
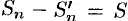
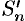
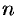
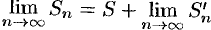
Аналогично рассуждаем в случае приписывания к ряду конечного числа членов.
называется 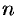
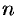
Из свойства 3 также следует, что если ряд (59.1) сходится, то его остаток 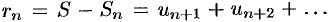
Лекции и примеры решения к этой теме:
Знакочередующиеся и знакопеременные ряды
Лекции и примеры решения к этой теме:
Степенные ряды
Лекции и примеры решения к этой теме:
Разложение функций в степенные ряды
Лекции и примеры решения к этой теме:
Ряды Фурье. Интеграл Фурье
Лекции и примеры решения к этой теме:
Элементы теории поля
Основные понятия теории поля
Теория поля — крупный раздел физики, механики, математики, в котором изучаются скалярные, векторные, тензорные поля.
К рассмотрению скалярных и векторных полей приводят многие задачи физики, электротехники, математики, механики и других технических дисциплин. Изучение одних физических полей способствует изучению и других. Так, например, силы всемирного тяготения, магнитные, электрические силы — все они изменяются обратно пропорционально квадрату расстояния от своего источника; диффузия в растворах происходит по законам, общим с распространением тепла в различных средах; вид силовых магнитных линий напоминает картину обтекания препятствий жидкостью и т. д.
Математическим ядром теории поля являются такие понятия, как градиент, поток, потенциал, дивергенция, ротор, циркуляция и другие. Эти понятия важны и в усвоении основных идей математического анализа функций многих переменных.
Полем называется область 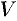
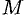
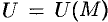
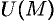
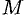
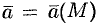
Примерами скалярных полей могут быть поля температуры (воздуха, тела, …), атмосферного давления, плотности (массы, воздуха, …), электрического потенциала и т. д. Примерами векторных полей являются поле силы тяжести, поле скоростей частиц текущей жидкости (ветра), магнитное папе, папе плотности электрического тока и т. д.
Если функция 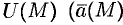
Далее будем рассматривать только стационарные паля.
Если 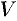

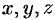
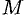
(Наряду с обозначениями 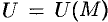
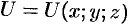
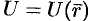
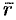
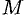
Если скалярная функция 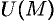


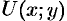
Аналогично: вектор 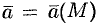



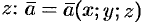
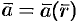
Вектор 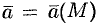
где 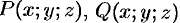
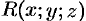
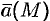
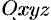
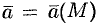
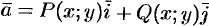
Векторное поле называется однородным, если 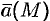
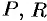
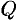
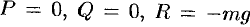
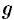
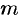
В дальнейшем будем предполагать, что скалярные функции ( 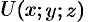
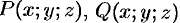
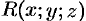
Пример №69.1.
Функция 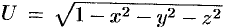
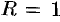
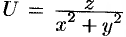
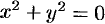
Скалярное поле
Лекции и примеры решения к этой теме:
Векторное поле
Лекции и примеры решения к этой теме:
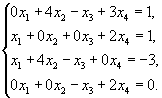
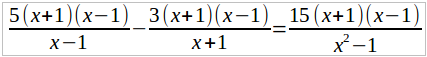
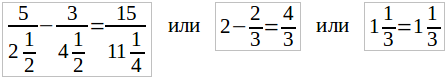
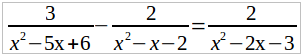
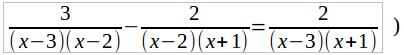


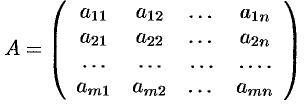
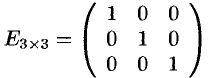
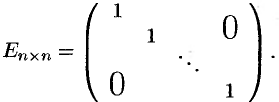
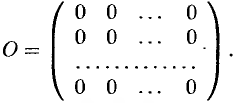
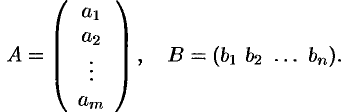
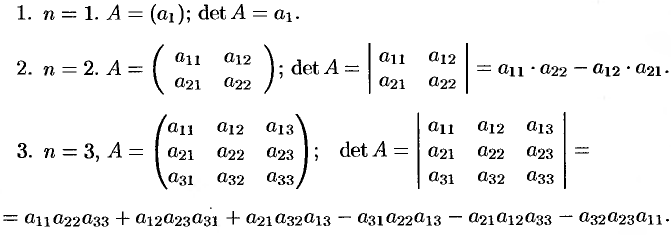
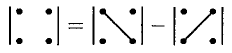
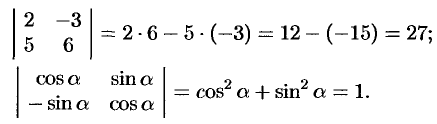
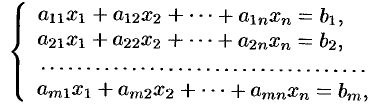
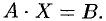

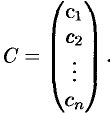
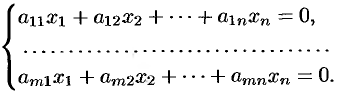
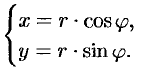
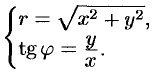
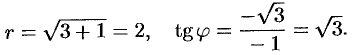
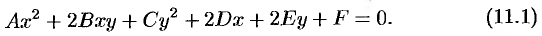
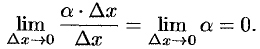


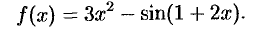
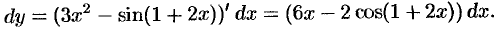
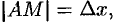
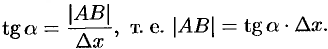
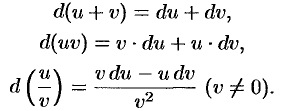
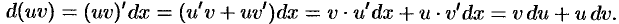
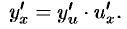
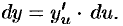
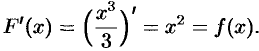
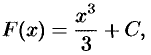
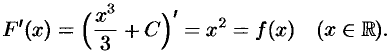
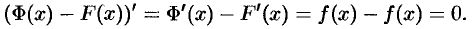
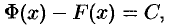
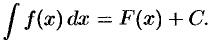
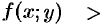

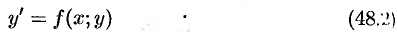
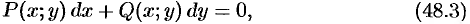

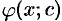 является решением ДУ при каждом фиксированном значении
является решением ДУ при каждом фиксированном значении 

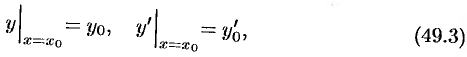
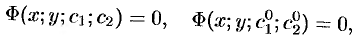
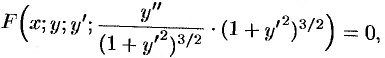
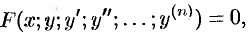
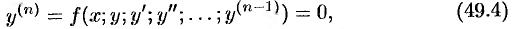
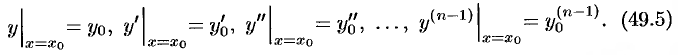
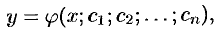
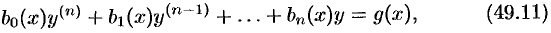
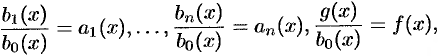
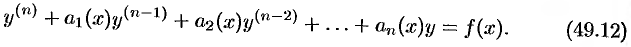
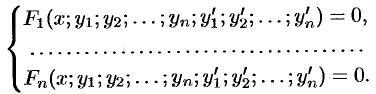
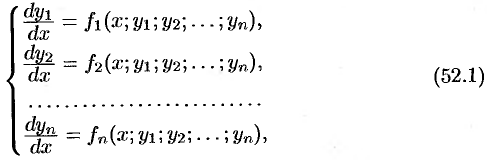
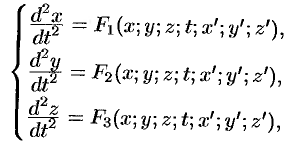
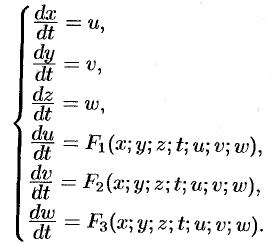
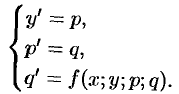
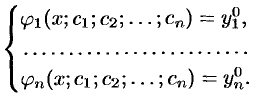
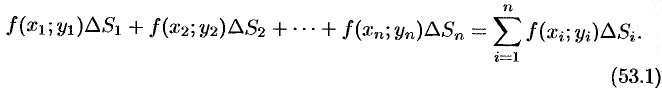
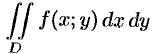
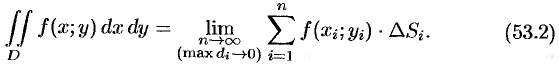
 , равенство (53.2) можно записать в виде
, равенство (53.2) можно записать в виде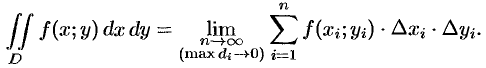
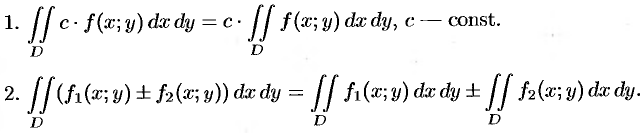
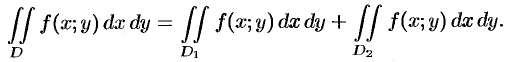
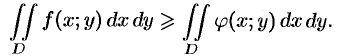
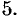
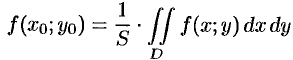
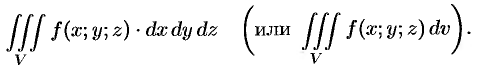
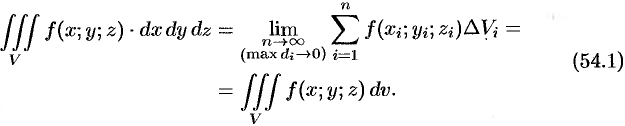
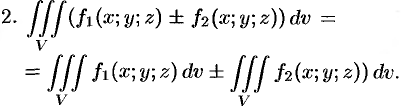
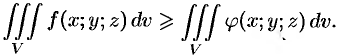
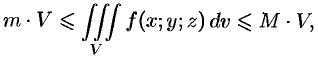
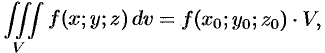
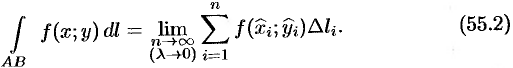
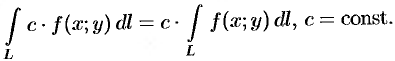
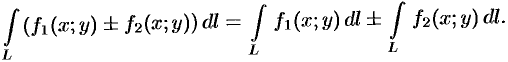
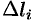
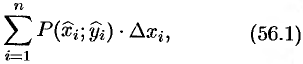
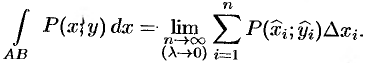
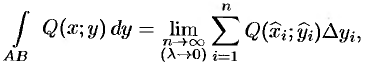
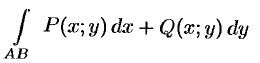
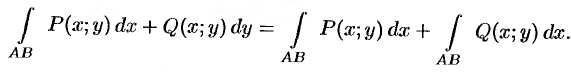
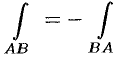
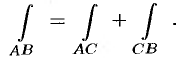
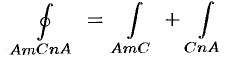
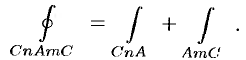
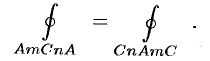

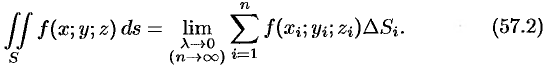
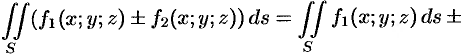
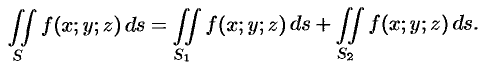
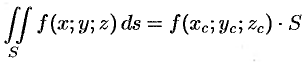
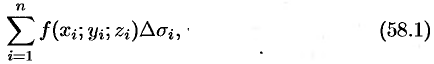
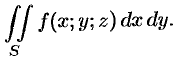
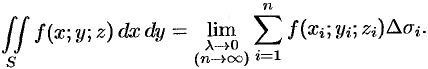
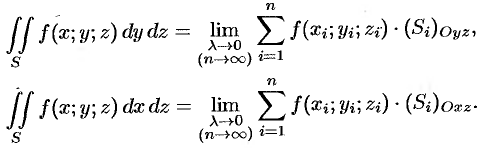
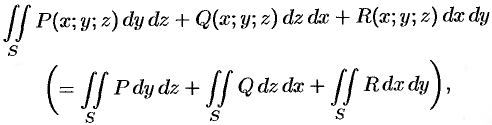
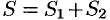 равен сумме интегралов по ее частям
равен сумме интегралов по ее частям  — цилиндрические поверхности с образующими, параллельными соответственно осям
— цилиндрические поверхности с образующими, параллельными соответственно осям  , то
, то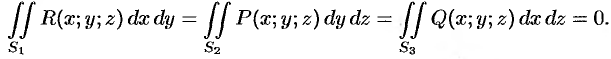
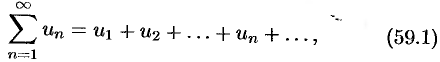
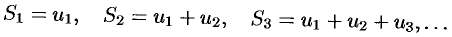
 нельзя считать заданным, а ряд 2 + 5 + 8 +… — можно: его общий член задастся формулой
нельзя считать заданным, а ряд 2 + 5 + 8 +… — можно: его общий член задастся формулой 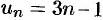 .
.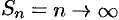 при
при 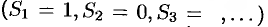 не имеет предела.
не имеет предела.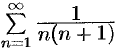 сходится. Действительно,
сходится. Действительно,