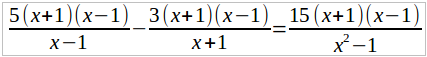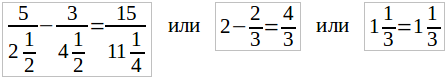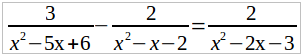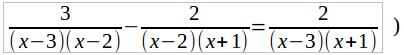Разделы: Математика
Класс: 10
Учебник: Колягин Ю. М. Алгебра и начала математического анализа. 10 класс. Москва, «Просвещение», 2014.
Урок проведён в универсальном 10-м классе средней общеобразовательной школы.
Цели урока: изучение способов решения показательных уравнений, тренировка в применении полученных знаний при решении заданий по теме, развитие творческой и мыслительной деятельности учащихся, формирование умения чётко и ясно излагать свои мысли, формирование познавательных интересов и мотивов самосовершенствования, воспитание умения работать с имеющейся информацией и культуры труда.
Структура урока
1. Организационный этап. Постановка темы и цели урока
– Прочитайте тему сегодняшнего урока (Приложение 1, слайд № 1)
– «Показательные уравнения».
– Нам это уже известно или это новый вид уравнений?
– Это новый вид уравнений.
– Попробуйте сформулировать цели урока.
– Мы узнаем, какие уравнения называются показательными, изучим способы их решения и будем учиться применять новое знание при решении задач по теме.
Учитель корректирует ответы учащихся.
2. Актуализация знаний. Устная работа (слайд № 3)
- Подберите корень уравнения 2 х = 32; 3 х = 27; 10 х = 10000
- Решите уравнение х 2 = 36; х 2 + х = 0; х 2 + 2х + 1 = 0
- Найдите область значений функции у = π х ; у = (0,5) х ; у = (0,5) |х|
- Сравните, используя свойства функций, с единицей 2 – 5 ; (0,5) – 3 ; (0,5) 0,5
3. Изучение нового материала (лекция)
Уравнение, в котором неизвестное содержится в показателе степени, считается показательным (слайд № 4). Рассмотрим основные виды показательных уравнений (слайд № 5) (учащиеся записывают названия видов и примеры в тетрадях).
1. Элементарные показательные уравнения. Эти уравнения сводятся к решению уравнений вида а х = а в , где а >0, а ≠ 1. При этом используется свойство степени, которое мы изучали (повторить следствие 2 на стр. 160 учебника). Рассмотрим примеры решения таких уравнений.
Пример 1 (слайд № 6).
(0,0016) 0,2 х + 1 = 25;
5 – 4 (0,2 х + 1) = 52;
– 0,8 х – 4 = 2;
– 0,8 х = 6;
х = – 7,5 .
Пример 2 (слайд №7)
36 · 6 х = 1;
6 2 + х = 60;
2 + х = 0;
х = – 2.
Пример 3 (слайд №8)
81 х · 2 4х = 36;
3 4х · 2 4х = 62;
6 4х = 6 2 ;
4х = 2;
х = 0,5.
Ответ: 0,5.
Пример 4 (слайд № 9)
2 х – 3 = 3 х – 3 ;
х – 3 = 0;
х = 3.
Ответ: 3.
2. Вынесение общего множителя за скобки (слайд № 10). Рассмотрим примеры решения таких уравнений.
2 · 3 х + 1 – 6 · 3 х – 1 – 3 х = 9;
3 х (2 · 3 – 6 · 3 – 1 – 1) = 9;
3 х · 3 = 9;
3 х = 3;
х = 3.
Ответ: 3.
Пример 2 (слайд № 11).
5 2х – 7 х – 5 2х · 17 + 7 х · 17 = 0;
5 2х – 5 2х · 17 = 7 х – 7 х · 17;
5 2х (1 – 17) = 7 х (1 – 17);
– 16· 52х = – 16 · 7х;
5 2х = 7 х ;
25 х = 7 х ;
х= 0.
Ответ: 0.
3. Сведение к квадратному уравнению (слайд № 12). Рассмотрим примеры решения таких уравнений.
9 х – 4 · 3 х = 45;
3 2х – 4 · 3 х – 45 = 0;
Замена 3 х = t, t > 0;
t 2 – 4 t – 45 = 0;
D = 16 +180 = 196;
t1 = 9,
t2 = – 5 – не удовлетворяет условию t > 0;
3 х = 9;
3 х = 32;
х = 2;
Ответ: 2.
4. Закрепление изученного материала
– Продолжаем учиться решать показательные уравнения. (Решение всех последующих уравнений записывается на доске с объяснениями, следует вызвать ученика по желанию). Разберём №680(3), 681(1), 682(3), 684(1), 693(2).
5. Обучающая самостоятельная работа с самопроверкой
– Предлагаю вам самостоятельно решить следующие уравнения (слайд № 13), а затем проверить себя самостоятельно с помощью готовых решений (решение уравнений следует заранее заготовить, например, на слайдах, а затем показать учащимся по окончании работы).
- (0,3) 5 – 2х = 0,09;
- 225 · 15 2х + 1 = 1;
- 3 х + 1 – 3 х = 18;
- 9 х – 26 · 3 х – 27 = 0
Решение № 1 (слайд № 14)
Решение № 2 (слайд № 15)
15 2 · 15 2х + 1 = 150;
152х + 3 = 150;
2х + 3 = 0;
х = – 1,5.
Ответ: – 1,5.
Решение № 3 (слайд № 16)
3 х · 3 – 3 х = 18;
3 х (3 – 1) = 18;
3 х · 2 = 18;
3 х = 9;
3 х = 3 2 ;
х = 2.
Ответ: х = 2.
Решение № 4 (слайд № 17)
3 2х – 26 · 3 х – 27 = 0;
Замена 3 х = t, t > 0;
t 2 – 26 t – 27 = 0;
t1 = 27,
t2 = – 1 не удовлетворяет условию t > 0;
3 х = 27; 3 х = 3 3 ; х = 3;
Ответ: 3.
6. Подведение итога урока. Рефлексия
– Итак, подведём итоги проделанной работы. Что нового вы узнали?
– С какими видами показательных уравнений мы познакомились?
7. Домашнее задание (слайд № 18)
Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать
Показательные уравнения
О чем эта статья:
6 класс, 7 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Сложные уравнения. Как решить сложное уравнение?Скачать
Определение показательного уравнения
Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.
Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:
Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.
С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a
Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.
Свойства степеней
Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.
Видео:Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать
Математика
52. Более сложные примеры уравнений.
Пример 1 .
5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)
Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:
или, после сокращения,
5(x + 1) – 3(x – 1) = 15
5x + 5 – 3x + 3 = 15
Рассмотрим еще уравнение:
5/(x-1) – 3/(x+1) = 4(x 2 – 1)
Решая, как выше, получим:
5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.
Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.
Для первого примера получим:
Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.
Для второго примера получим:
5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0
Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.
Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.
(x + 3)/(x – 1) = (2x + 3)/(2x – 2)
Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:
(x + 3) (2x – 2) = (2x + 3) (x – 1)
2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.
Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:
6x – 2x – 6 = 3x – 2x – 3
Перенесем неизвестные члены влево, известные вправо — получим:
Вспоминая данное уравнение
(x + 3)/(x – 1) = (2x + 3)/(2x – 2)
мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.
Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:
2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,
Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:
(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)
Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:
Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:
или 11 = 11
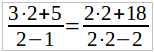
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:
(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.
Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы
Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:
1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2
Если мы вспомним начальное уравнение
(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),
то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.
Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:
1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),
2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),
3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).
Общий знаменатель равен (x – 3)(x – 2)(x + 1).
Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:
на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:
3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.
Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.
Если бы мы взяли уравнение:
то, поступая совершенно так же, как выше, получили бы
3(x + 1) – 2(x – 3) = x – 2
3x + 3 – 2x + 6 = x – 2
3x – 2x – x = –3 – 6 – 2,
откуда получили бы
что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.
📹 Видео
СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать
Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать
Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать
10 класс. Алгебра. Системы уравненийСкачать
Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Тригонометрия для Чайников, 10 класс, Уравнения, Урок 7Скачать
Как решать дробно-рациональные уравнения? | МатематикаСкачать
Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать
СИСТЕМА УРАВНЕНИЙ различные способы решения 9 10 класс алгебраСкачать
ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать
ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать
Алгебра 10 класс (Урок№19 - Равносильные уравнения и неравенства.)Скачать
Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать
ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать
Умножаем логарифмы В УМЕ🧠Скачать
