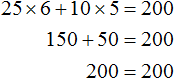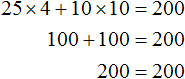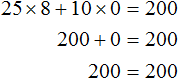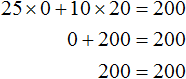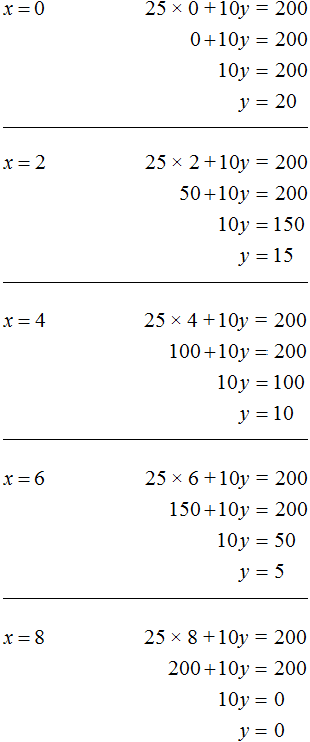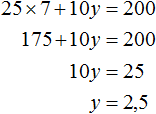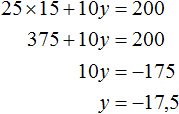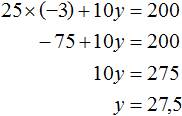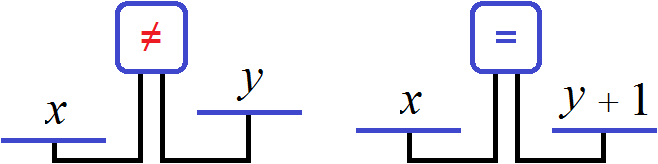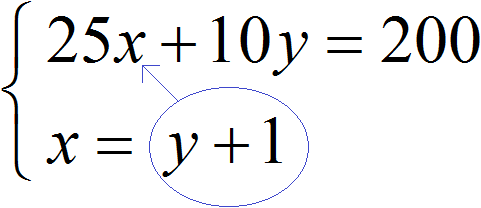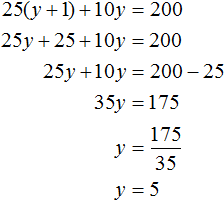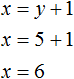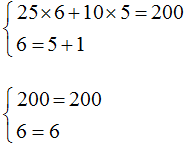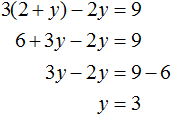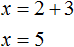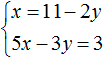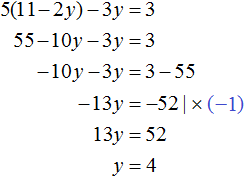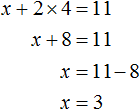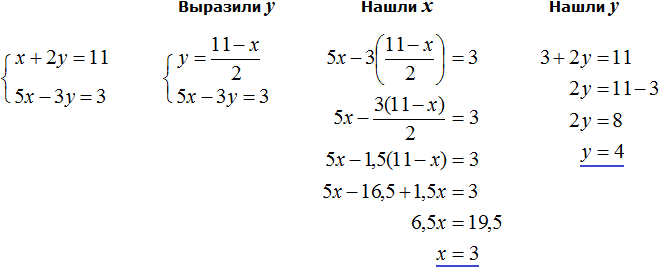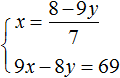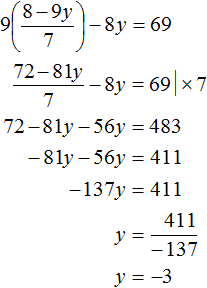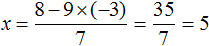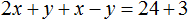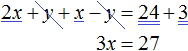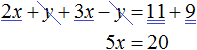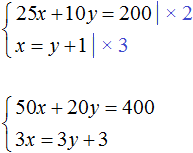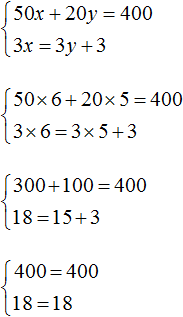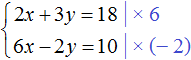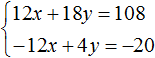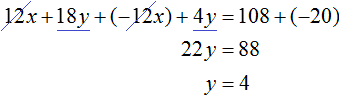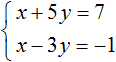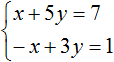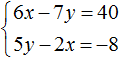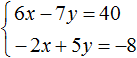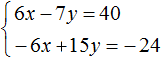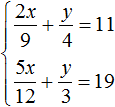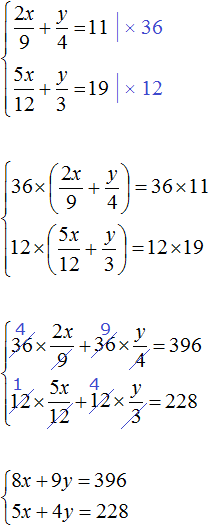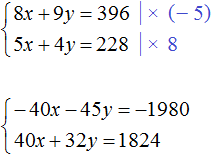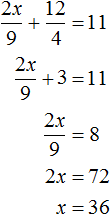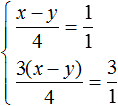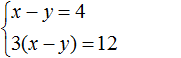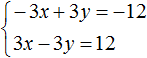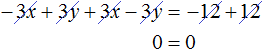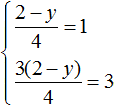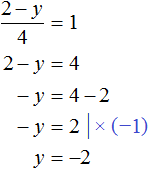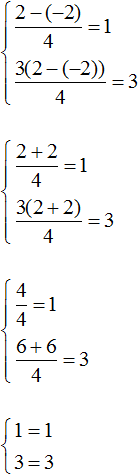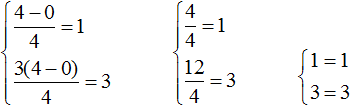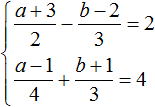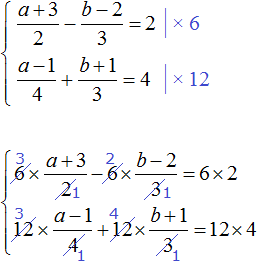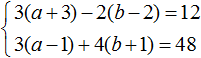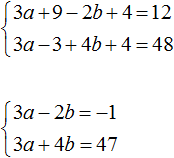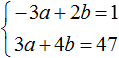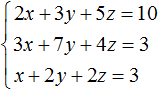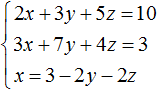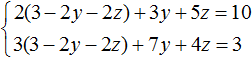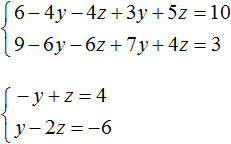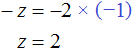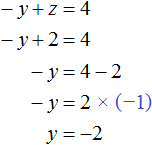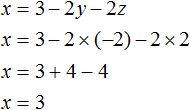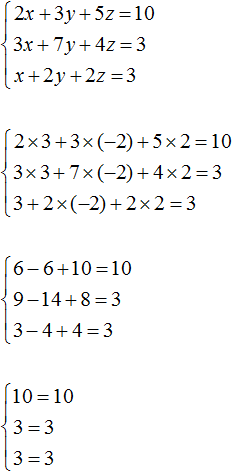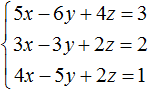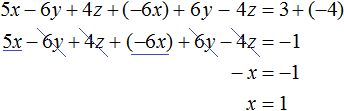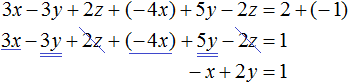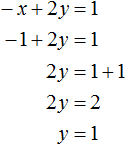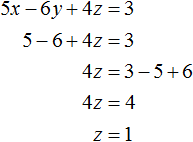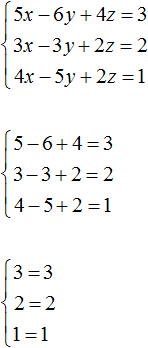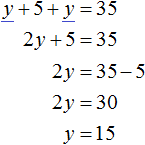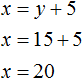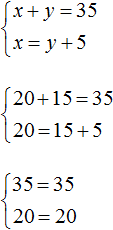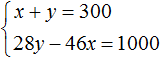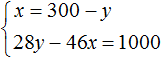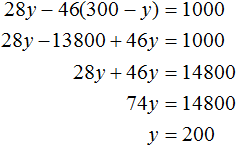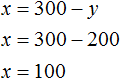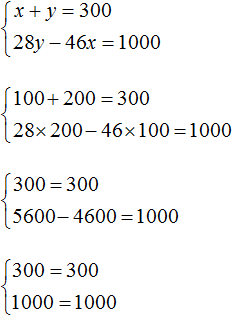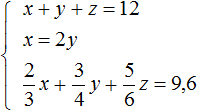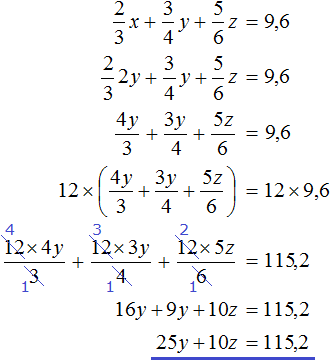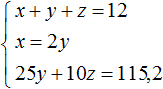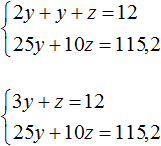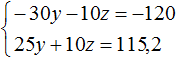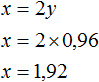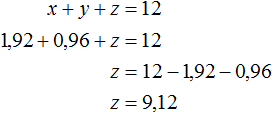- Если несколько линейных уравнений с одними теми же неизвестными рассматривают совместно, то говорят, что это система линейных уравнений с несколькими неизвестными.
- Решить систему с двумя неизвестными – это значит найти все пары значений переменных, которые удовлетворяют каждому из заданных уравнений. Каждая такая пара называется решением системы.
- Как решить систему линейных уравнений?
- Системы линейных уравнений
- Линейные уравнения с двумя переменными
- Система двух линейных уравнений с двумя переменными
- Метод подстановки
- Метод сложения
- Система линейных уравнений с тремя переменными
- Задачи на составление систем линейных уравнений
- Задания по теме Системы уравнений
- Краткое описание документа:
- Математика: теория и методика преподавания в образовательной организации
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 🎥 Видео
Если несколько линейных уравнений с одними теми же неизвестными рассматривают совместно, то говорят, что это система линейных уравнений с несколькими неизвестными.
Решить систему с двумя неизвестными – это значит найти все пары значений переменных, которые удовлетворяют каждому из заданных уравнений. Каждая такая пара называется решением системы.
Пример:
Пара значений (x=3);(y=-1) является решением первой системы, потому что при подстановке этих тройки и минус единицы в вместо (x) и (y), оба уравнения превратятся в верные равенства (begin3-2cdot (-1)=5 \3 cdot 3+2 cdot (-1)=7 end)
А вот (x=1); (y=-2) — не является решением первой системы, потому что после подстановки второе уравнение «не сходится» (begin1-2cdot(-2)=5 \3cdot1+2cdot(-2)≠7 end)
Отметим, что такие пары часто записывают короче: вместо «(x=3); (y=-1)» пишут так: ((3;-1)).
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Как решить систему линейных уравнений?
Есть три основных способа решения систем линейных уравнений:
Возьмите любое из уравнений системы и выразите из него любую переменную.
Полученное выражение подставьте вместо этой переменной в другое линейное уравнение системы.
Ответ запишите парой чисел ((x_0;y_0))
Замечание к шагу 1: нет никакой разницы какую переменную и из какого уравнения выражать. Обычно более удобно выражать ту переменную, перед которой нет коэффициента или, говоря точнее, коэффициент которой равен единице (в примере выше это был икс в первом уравнении).
Почему так? Потому что во всех остальных случаях у нас при выражении переменной получилась бы дробное выражение . Попробуем, например, выразить икс из второго уравнения системы:
И сейчас нам нужно будет эту дробь подставлять в первое уравнение и решать то, что получиться. До верного ответа мы бы всё равно дошли, но идти было бы неудобнее
Способ алгебраического сложения.
Равносильно преобразовывая каждое уравнение в отдельности, запишите систему в виде:(begina_1 x+b_1 y=c_1\a_2 x+b_2 y=c_2end).
Теперь нужно сделать так, чтоб коэффициенты при одном из неизвестных стали одинаковы (например, ((3) и (3)) или противоположны по значению (например, (5) и (-5)). В нашем примере уравняем коэффициенты при игреках. Для этого первое уравнение домножим на (2), а второе — на (3).
(begin2x+3y=13 |cdot 2\ 5x+2y=5 |cdot 3end)(Leftrightarrow)(begin4x+6y=26\15x+6y=15end)(Leftrightarrow)
Сложите (или вычтите) почленно обе части уравнения так, чтобы получилось уравнение с одним неизвестным.
Найдите неизвестное из полученного уравнения.
Подставьте найденное значение неизвестного в любое из исходных уравнений и найдите второе неизвестное.
Ответ запишите парой чисел ((x_0;y_0)).
Замечание к шагу 3: В каком случае уравнения складывают, а в каком вычитают? Ответ прост – делайте так, чтоб пропала переменная: если «уравненные» коэффициенты имеют один и тот же знак – вычитайте, а если разные – складывайте.
Пример. Решите систему уравнений: (begin12x-7y=2\5y=4x-6end)
Приводим систему к виду (begina_1 x+b_1 y=c_1\a_2 x+b_2 y=c_2end) преобразовывая второе уравнение.
«Уравняем» коэффициенты при иксах. Для этого домножим второе уравнение на (3).
Знаки при иксах разные, поэтому чтоб иксы пропали, уравнения надо сложить.
Делим уравнение на (8), чтобы найти (y).
Игрек нашли. Теперь найдем (x), подставив вместо игрека (-2) в любое из уравнений системы.
Икс тоже найден. Пишем ответ.
Приведите каждое уравнение к виду линейной функции (y=kx+b).
Постройте графики этих функций. Как? Можете прочитать здесь .
Ответ: ((4;2))
Матхак. Если сомневаетесь в правильности ответа (неважно каким способом вы решали), проверьте подстановкой значений (x_0) и (y_0) в каждое уравнение. Если оба уравнения превратятся в верные равенства, то ответ правильный.
Пример: решая систему (begin3x-8=2y\x+y=6end), мы получили ответ ((4;2)). Проверим его, подставив вместо икса (4), а вместо игрека (2).
Оба уравнения сошлись, решение системы найдено верно.
Пример. Решите систему уравнений: (begin3(5x+3y)-6=2x+11\4x-15=11-2(4x-y)end)
Перенесем все выражения с буквами в одну сторону, а числа в другую.
Во втором уравнении каждое слагаемое — четное, поэтому упрощаем уравнение, деля его на (2).
Эту систему линейных уравнений можно решить любым из способов, но мне кажется, что способ подстановки здесь удобнее всего. Выразим y из второго уравнения.
Подставим (6x-13) вместо (y) в первое уравнение.
Первое уравнение превратилась в обычное линейное . Решаем его.
Сначала раскроем скобки.
Перенесем (117) вправо и приведем подобные слагаемые.
Поделим обе части первого уравнения на (67).
Ура, мы нашли (x)! Подставим его значение во второе уравнение и найдем (y).
Видео:7 класс, 39 урок, Метод алгебраического сложенияСкачать

Системы линейных уравнений
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Линейные уравнения с двумя переменными
У школьника имеется 200 рублей, чтобы пообедать в школе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе можно накупить на 200 рублей?
Обозначим количество пирожных через x , а количество чашек кофе через y . Тогда стоимость пирожных будет обозначаться через выражение 25x , а стоимость чашек кофе через 10y .
25x — стоимость x пирожных
10y — стоимость y чашек кофе
Итоговая сумма должна равняться 200 рублей. Тогда получится уравнение с двумя переменными x и y
Сколько корней имеет данное уравнение?
Всё зависит от аппетита школьника. Если он купит 6 пирожных и 5 чашек кофе, то корнями уравнения будут числа 6 и 5.
Говорят, что пара значений 6 и 5 являются корнями уравнения 25x + 10y = 200 . Записывается как (6; 5) , при этом первое число является значением переменной x , а второе — значением переменной y .
6 и 5 не единственные корни, которые обращают уравнение 25x + 10y = 200 в тождество. При желании на те же 200 рублей школьник может купить 4 пирожных и 10 чашек кофе:
В этом случае корнями уравнения 25x + 10y = 200 является пара значений (4; 10) .
Более того, школьник может вообще не покупать кофе, а купить пирожные на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 8 и 0
Или наоборот, не покупать пирожные, а купить кофе на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 0 и 20
Попробуем перечислить все возможные корни уравнения 25x + 10y = 200 . Условимся, что значения x и y принадлежат множеству целых чисел. И пусть эти значения будут бóльшими или равными нулю:
Так будет удобно и самому школьнику. Пирожные удобнее покупать целыми, чем к примеру несколько целых пирожных и половину пирожного. Кофе также удобнее брать целыми чашками, чем к примеру несколько целых чашек и половину чашки.
Заметим, что при нечетном x невозможно достичь равенства ни при каком y . Тогда значениями x будут следующие числа 0, 2, 4, 6, 8. А зная x можно без труда определить y
Таким образом, мы получили следующие пары значений (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Эти пары являются решениями или корнями уравнения 25x + 10y = 200 . Они обращают данное уравнение в тождество.
Уравнение вида ax + by = c называют линейным уравнением с двумя переменными. Решением или корнями этого уравнения называют пару значений ( x; y ), которая обращает его в тождество.
Отметим также, что если линейное уравнение с двумя переменными записано в виде ax + b y = c , то говорят, что оно записано в каноническом (нормальном) виде.
Некоторые линейные уравнения с двумя переменными могут быть приведены к каноническому виду.
Например, уравнение 2(16x + 3y − 4) = 2(12 + 8x − y) можно привести к виду ax + by = c . Раскроем скобки в обеих частях этого уравнения, получим 32x + 6y − 8 = 24 + 16x − 2y . Слагаемые, содержащие неизвестные сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой. Тогда получим 32x − 16x + 6y + 2y = 24 + 8 . Приведём подобные слагаемые в обеих частях, получим уравнение 16x + 8y = 32. Это уравнение приведено к виду ax + by = c и является каноническим.
Рассмотренное ранее уравнение 25x + 10y = 200 также является линейным уравнением с двумя переменными в каноническом виде . В этом уравнении параметры a , b и c равны значениям 25, 10 и 200 соответственно.
На самом деле уравнение ax + by = c имеет бесчисленное множество решений. Решая уравнение 25x + 10y = 200, мы искали его корни только на множестве целых чисел. В результате получили несколько пар значений, которые обращали данное уравнение в тождество. Но на множестве рациональных чисел уравнение 25x + 10y = 200 будет иметь бесчисленное множество решений.
Для получения новых пар значений, нужно взять произвольное значение для x , затем выразить y . К примеру, возьмем для переменной x значение 7. Тогда получим уравнение с одной переменной 25 × 7 + 10y = 200 в котором можно выразить y
Пусть x = 15 . Тогда уравнение 25x + 10y = 200 примет вид 25 × 15 + 10y = 200. Отсюда находим, что y = −17,5
Пусть x = −3 . Тогда уравнение 25x + 10y = 200 примет вид 25 × (−3) + 10y = 200. Отсюда находим, что y = 27,5
Видео:Решение системы линейных уравнений графическим способом. 7 классСкачать

Система двух линейных уравнений с двумя переменными
Для уравнения ax + by = c можно сколько угодно раз брать произвольные значение для x и находить значения для y . Отдельно взятое такое уравнение будет иметь бесчисленное множество решений.
Но бывает и так, что переменные x и y связаны не одним, а двумя уравнениями. В этом случае они образуют так называемую систему линейных уравнений с двумя переменными. Такая система уравнений может иметь одну пару значений (или по-другому: «одно решение»).
Может случиться и так, что система вовсе не имеет решений. Бесчисленное множество решений система линейных уравнений может иметь в редких и в исключительных случаях.
Два линейных уравнения образуют систему тогда, когда значения x и y входят в каждое из этих уравнений.
Вернемся к самому первому уравнению 25x + 10y = 200 . Одной из пар значений для этого уравнения была пара (6; 5) . Это случай, когда на 200 рублей можно можно было купить 6 пирожных и 5 чашек кофе.
Составим задачу так, чтобы пара (6; 5) стала единственным решением для уравнения 25x + 10y = 200 . Для этого составим ещё одно уравнение, которое связывало бы те же x пирожных и y чашечек кофе.
Поставим текст задачи следующим образом:
«Школьник купил на 200 рублей несколько пирожных и несколько чашек кофе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе купил школьник, если известно что количество пирожных на одну единицу больше количества чашек кофе?»
Первое уравнение у нас уже есть. Это уравнение 25x + 10y = 200 . Теперь составим уравнение к условию «количество пирожных на одну единицу больше количества чашек кофе» .
Количество пирожных это x , а количество чашек кофе это y . Можно записать эту фразу с помощью уравнения x − y = 1. Это уравнение будет означать, что разница между пирожными и кофе составляет 1.
Либо второе уравнение можно записать как x = y + 1 . Это уравнение означает, что количество пирожных на единицу больше, чем количество чашек кофе. Поэтому для получения равенства, к количеству чашек кофе прибавлена единица. Это легко можно понять, если воспользоваться моделью весов, которые мы рассматривали при изучении простейших задач:
Получили два уравнения: 25x + 10y = 200 и x = y + 1. Поскольку значения x и y , а именно 6 и 5 входят в каждое из этих уравнений , то вместе они образуют систему. Запишем эту систему. Если уравнения образуют систему, то они обрамляются знаком системы. Знак системы это фигурная скобка:
Давайте решим данную систему. Это позволит увидеть, как мы придём к значениям 6 и 5. Существует много методов решения таких систем. Рассмотрим наиболее популярные из них.
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Метод подстановки
Название этого метода говорит само за себя. Суть его заключается в том, чтобы одно уравнение подставить в другое, предварительно выразив одну из переменных.
В нашей системе ничего выражать не нужно. Во втором уравнении x = y + 1 переменная x уже выражена. Эта переменная равна выражению y + 1 . Тогда можно подставить это выражение в первое уравнение вместо переменной x
После подстановки выражения y + 1 в первое уравнение вместо x , получим уравнение 25(y + 1) + 10y = 200 . Это линейное уравнение с одной переменной. Такое уравнение решить довольно просто:
Мы нашли значение переменной y . Теперь подставим это значение в одно из уравнений и найдём значение x . Для этого удобно использовать второе уравнение x = y + 1 . В него и подставим значение y
Значит пара (6; 5) является решением системы уравнений, как мы и задумывали. Выполняем проверку и убеждаемся, что пара (6; 5) удовлетворяет системе:
Пример 2. Решить методом подстановки следующую систему уравнений:
Подставим первое уравнение x = 2 + y во второе уравнение 3x − 2y = 9 . В первом уравнении переменная x равна выражению 2 + y . Это выражение и подставим во второе уравнение вместо x
Теперь найдём значение x . Для этого подставим значение y в первое уравнение x = 2 + y
Значит решением системы 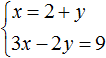
Пример 3. Решить методом подстановки следующую систему уравнений:
Здесь в отличие от предыдущих примеров, одна из переменных не выражена явно.
Чтобы подставить одно уравнение в другое, сначала нужно выразить одну из переменных.
Выражать желательно ту переменную, которая имеет коэффициент единицу. Коэффициент единицу имеет переменная x , которая содержится в первом уравнении x + 2y = 11 . Эту переменную и выразим.
После выражения переменной x , наша система примет следующий вид:
Теперь подставим первое уравнение во второе и найдем значение y
Подставим y в первое уравнение и найдём x
Значит решением системы 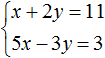
Конечно, выражать можно и переменную y . Корни от этого не изменятся. Но если выразить y, получится не очень-то и простое уравнение, на решение которого уйдет больше времени. Выглядеть это будет следующим образом:
Видим, что в данном примере выражать x намного удобнее, чем выражать y .
Пример 4. Решить методом подстановки следующую систему уравнений:
Выразим в первом уравнении x . Тогда система примет вид:
Подставим первое уравнение во второе и найдём y
Подставим y в первое уравнение и найдём x . Можно воспользоваться изначальным уравнением 7x + 9y = 8 , либо воспользоваться уравнением 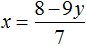
Значит решением системы 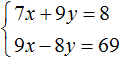
Видео:Система уравнений. Метод алгебраического сложенияСкачать

Метод сложения
Метод сложения заключается в том, чтобы почленно сложить уравнения, входящие в систему. Это сложение приводит к тому, что образуется новое уравнение с одной переменной. А решить такое уравнение довольно просто.
Решим следующую систему уравнений:
Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. Получим следующее равенство:
Приведем подобные слагаемые:
В результате получили простейшее уравнение 3x = 27 корень которого равен 9. Зная значение x можно найти значение y . Подставим значение x во второе уравнение x − y = 3 . Получим 9 − y = 3 . Отсюда y = 6 .
Значит решением системы 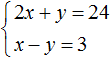
Пример 2. Решить следующую систему уравнений методом сложения:
Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. В получившемся равенстве приведем подобные слагаемые:
В результате получили простейшее уравнение 5 x = 20, корень которого равен 4. Зная значение x можно найти значение y . Подставим значение x в первое уравнение 2 x + y = 11 . Получим 8 + y = 11 . Отсюда y = 3 .
Значит решением системы 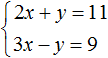
Процесс сложения подробно не расписывают. Его нужно выполнять в уме. При сложении оба уравнения должны быть приведены к каноническому виду. То есть к виду ax + by = c .
Из рассмотренных примеров видно, что основная цель сложения уравнений это избавление от одной из переменных. Но не всегда удаётся сразу решить систему уравнений методом сложения. Чаще всего систему предварительно приводят к виду, при котором можно сложить уравнения, входящие в эту систему.
Например, систему 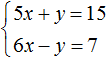
А систему уравнений 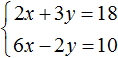
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному. Это правило справедливо и для системы линейных уравнений с двумя переменными. Одно из уравнений (или оба уравнения) можно умножить на какое-нибудь число. В результате получится равносильная система, корни которой будут совпадать с предыдущей.
Вернемся к самой первой системе 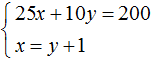
Умножим оба уравнения, входящие в эту систему на какие-нибудь числа. Скажем первое уравнение умножим на 2, а второе на 3
В результате получили систему 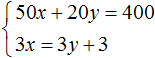
Решением этой системы по-прежнему является пара значений (6; 5)
Это значит, что уравнения входящие в систему можно привести к виду, пригодному для применения метода сложения.
Вернемся к системе 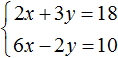
Умножим первое уравнение на 6, а второе на −2
Тогда получим следующую систему:
Сложим уравнения, входящие в эту систему. Сложение компонентов 12x и −12x даст в результате 0, сложение 18y и 4y даст 22y , а сложение 108 и −20 даст 88. Тогда получится уравнение 22y = 88 , отсюда y = 4 .
Если первое время тяжело складывать уравнения в уме, то можно записывать как складывается левая часть первого уравнения с левой частью второго уравнения, а правая часть первого уравнения с правой частью второго уравнения:
Зная, что значение переменной y равно 4, можно найти значение x. Подставим y в одно из уравнений, например в первое уравнение 2x + 3y = 18 . Тогда получим уравнение с одной переменной 2x + 12 = 18 . Перенесем 12 в правую часть, изменив знак, получим 2x = 6 , отсюда x = 3 .
Пример 4. Решить следующую систему уравнений методом сложения:
Умножим второе уравнение на −1. Тогда система примет следующий вид:
Сложим оба уравнения. Сложение компонентов x и −x даст в результате 0, сложение 5y и 3y даст 8y , а сложение 7 и 1 даст 8. В результате получится уравнение 8y = 8 , корень которого равен 1. Зная, что значение y равно 1, можно найти значение x .
Подставим y в первое уравнение, получим x + 5 = 7 , отсюда x = 2
Пример 5. Решить следующую систему уравнений методом сложения:
Желательно, чтобы слагаемые содержащие одинаковые переменные, располагались друг под другом. Поэтому во втором уравнении слагаемые 5y и −2x поменяем местами. В результате система примет вид:
Умножим второе уравнение на 3. Тогда система примет вид:
Теперь сложим оба уравнения. В результате сложения получим уравнение 8y = 16 , корень которого равен 2.
Подставим y в первое уравнение, получим 6x − 14 = 40 . Перенесем слагаемое −14 в правую часть, изменив знак, получим 6x = 54 . Отсюда x = 9.
Пример 6. Решить следующую систему уравнений методом сложения:
Избавимся от дробей. Умножим первое уравнение на 36, а второе на 12
В получившейся системе 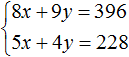
Сложим уравнения в получившейся системе. Тогда получим простейшее уравнение −13y = −156 . Отсюда y = 12 . Подставим y в первое уравнение и найдем x
Пример 7. Решить следующую систему уравнений методом сложения:
Приведем оба уравнения к нормальному виду. Здесь удобно применить правило пропорции в обоих уравнениях. Если в первом уравнении правую часть представить как 

У нас получилась пропорция. Перемножим её крайние и средние члены. Тогда система примет вид:
Первое уравнение умножим на −3, а во втором раскроем скобки:
Теперь сложим оба уравнения. В результате сложения этих уравнений, мы получим равенство, в обеих частях которого будет ноль:
Получается, что система 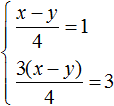
Но мы не можем просто так взять с неба произвольные значения для x и y . Мы можем указать одно из значений, а другое определится в зависимости от значения, указанного нами. Например, пусть x = 2 . Подставим это значение в систему:
В результате решения одного из уравнений, определится значение для y , которое будет удовлетворять обоим уравнениям:
Получившаяся пара значений (2; −2) будет удовлетворять системе:
Найдём еще одну пару значений. Пусть x = 4. Подставим это значение в систему:
На глаз можно определить, что значение y равно нулю. Тогда получим пару значений (4; 0), которая удовлетворяет нашей системе:
Пример 8. Решить следующую систему уравнений методом сложения:
Умножим первое уравнение на 6, а второе на 12
Перепишем то, что осталось:
Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:
Первое уравнение умножим на −1. Тогда система примет вид:
Теперь сложим оба уравнения. В результате сложения образуется уравнение 6b = 48 , корень которого равен 8. Подставим b в первое уравнение и найдём a
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Система линейных уравнений с тремя переменными
В линейное уравнение с тремя переменными входит три переменные с коэффициентами, а также свободный член. В каноническом виде его можно записать следующим образом:
Данное уравнение имеет бесчисленное множество решений. Придавая двум переменным различные значения, можно найти третье значение. Решением в этом случае является тройка значений (x; y; z) которая обращает уравнение в тождество.
Если переменные x, y, z связаны между собой тремя уравнениями, то образуется система трех линейных уравнений с тремя переменными. Для решения такой системы можно применять те же методы, которые применяются к линейным уравнениям с двумя переменными: метод подстановки и метод сложения.
Пример 1. Решить следующую систему уравнений методом подстановки:
Выразим в третьем уравнении x . Тогда система примет вид:
Теперь выполним подстановку. Переменная x равна выражению 3 − 2y − 2z . Подставим это выражение в первое и второе уравнение:
Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:
Мы пришли к системе линейных уравнений с двумя переменными. В данном случае удобно применить метод сложения. В результате переменная y исчезнет, и мы сможем найти значение переменной z
Теперь найдём значение y . Для этого удобно воспользоваться уравнением −y + z = 4. Подставим в него значение z
Теперь найдём значение x . Для этого удобно воспользоваться уравнением x = 3 − 2y − 2z . Подставим в него значения y и z
Таким образом, тройка значений (3; −2; 2) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:
Пример 2. Решить систему методом сложения
Сложим первое уравнение со вторым, умноженным на −2.
Если второе уравнение умножить на −2, то оно примет вид −6x + 6y − 4z = −4 . Теперь сложим его с первым уравнением:
Видим, что в результате элементарных преобразований, определилось значение переменной x . Оно равно единице.
Вернемся к главной системе. Сложим второе уравнение с третьим, умноженным на −1. Если третье уравнение умножить на −1, то оно примет вид −4x + 5y − 2z = −1 . Теперь сложим его со вторым уравнением:
Получили уравнение x − 2y = −1 . Подставим в него значение x , которое мы находили ранее. Тогда мы сможем определить значение y
Теперь нам известны значения x и y . Это позволяет определить значение z . Воспользуемся одним из уравнений, входящим в систему:
Таким образом, тройка значений (1; 1; 1) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:
Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Задачи на составление систем линейных уравнений
Задача на составление систем уравнений решается путем ввода нескольких переменных. Далее составляются уравнения на основании условий задачи. Из составленных уравнений образуют систему и решают её. Решив систему, необходимо выполнить проверку на то, удовлетворяет ли её решение условиям задачи.
Задача 1. Из города в колхоз выехала машина «Волга». Обратно она возвращалась по другой дороге, которая была на 5 км короче первой. Всего в оба конца машина проехала 35 км. Сколько километров составляет длина каждой дороги?
Решение
Пусть x — длина первой дороги, y — длина второй. Если в оба конца машина проехала 35 км, то первое уравнение можно записать как x + y = 35. Это уравнение описывает сумму длин обеих дорог.
Сказано, что обратно машина возвращалась по дороге которая была короче первой на 5 км. Тогда второе уравнение можно записать как x − y = 5. Это уравнение показывает, что разница между длинами дорог составляет 5 км.
Либо второе уравнение можно записать как x = y + 5 . Этим уравнением и воспользуемся.
Поскольку переменные x и y в обоих уравнениях обозначают одно и то же число, то мы можем образовать из них систему:
Решим эту систему каким-нибудь из изученных ранее методов. В данном случае удобно воспользоваться методом подстановки, поскольку во втором уравнении переменная x уже выражена.
Подставим второе уравнение в первое и найдём y
Подставим найденное значение y в во второе уравнение x = y + 5 и найдём x
Длина первой дороги была обозначена через переменную x . Теперь мы нашли её значение. Переменная x равна 20. Значит длина первой дороги составляет 20 км.
А длина второй дороги была обозначена через y . Значение этой переменной равно 15. Значит длина второй дороги составляет 15 км.
Выполним проверку. Для начала убедимся, что система решена правильно:
Теперь проверим удовлетворяет ли решение (20; 15) условиям задачи.
Было сказано, что всего в оба конца машина проехала 35 км. Складываем длины обеих дорог и убеждаемся, что решение (20; 15) удовлетворяет данному условию: 20 км + 15 км = 35 км
Следующее условие: обратно машина возвращалась по другой дороге, которая была на 5 км короче первой . Видим, что решение (20; 15) удовлетворяет и этому условию, поскольку 15 км короче, чем 20 км на 5 км: 20 км − 15 км = 5 км
При составлении системы важно, чтобы переменные обозначали одни и те же числа во всех уравнениях, входящих в эту систему.
Так наша система 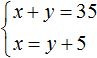
Задача 2. На платформу были погружены дубовые и сосновые шпалы, всего 300 шпал. Известно, что все дубовые шпалы весили на 1 т меньше, чем все сосновые. Определить, сколько было дубовых и сосновых шпал отдельно, если каждая дубовая шпала весила 46 кг, а каждая сосновая 28 кг.
Решение
Пусть x дубовых и y сосновых шпал было погружено на платформу. Если всего шпал было 300, то первое уравнение можно записать как x + y = 300 .
Все дубовые шпалы весили 46x кг, а сосновые весили 28y кг. Поскольку дубовые шпалы весили на 1 т меньше, чем сосновые, то второе уравнение можно записать, как 28y − 46x = 1000 . Это уравнение показывает, что разница масс между дубовыми и сосновыми шпалами, составляет 1000 кг.
В результате получаем два уравнения, которые образуют систему
Решим данную систему. Выразим в первом уравнении x . Тогда система примет вид:
Подставим первое уравнение во второе и найдём y
Подставим y в уравнение x = 300 − y и узнаем чему равно x
Значит на платформу было погружено 100 дубовых и 200 сосновых шпал.
Проверим удовлетворяет ли решение (100; 200) условиям задачи. Для начала убедимся, что система решена правильно:
Было сказано, что всего было 300 шпал. Складываем количество дубовых и сосновых шпал и убеждаемся, что решение (100; 200) удовлетворяет данному условию: 100 + 200 = 300.
Следующее условие: все дубовые шпалы весили на 1 т меньше, чем все сосновые . Видим, что решение (100; 200) удовлетворяет и этому условию, поскольку 46 × 100 кг дубовых шпал легче, чем 28 × 200 кг сосновых шпал: 5600 кг − 4600 кг = 1000 кг.
Задача 3. Взяли три куска сплава меди с никелем в отношениях 2 : 1 , 3 : 1 и 5 : 1 по массе. Из них сплавлен кусок массой 12 кг с отношением содержания меди и никеля 4 : 1 . Найдите массу каждого исходного куска, если масса первого из них вдвое больше массы второго.
Решение
Пусть x — масса первого куска, y — масса второго куска, z — масса третьего куска. Если из этих кусков сплавлен кусок массой 12 кг, то первое уравнение можно записать как x + y + z = 12 .
Масса первого куска вдвое больше массы второго куска. Тогда второе уравнение можно записать как x = 2y .
Полученных двух уравнений недостаточно для решения данной задачи. Если второе уравнение подставить в первое, то мы получим уравнение 2y + y + z = 12 , откуда 3y + z = 12 . Это уравнение имеет бесчисленное множество решений.
Составим ещё одно уравнение. Пусть это уравнение будет описывать количество меди, взятого с каждого сплава и сколько меди оказалось в получившемся сплаве.
Если первый сплав имеет массу x , а медь и никель находится нём в отношении 2 : 1 , то можно записать, что в новом сплаве содержится 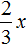
Если второй сплав имеет массу y , а медь и никель находится в нём в отношении 3 : 1 , то можно записать, что в новом сплаве содержится 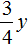
Если третий сплав имеет массу z , а медь и никель находится в отношении 5 : 1 , то можно записать, что в новом сплаве содержится 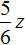
Полученный сплав имеет имеет массу 12 кг, а медь и никель находится в нём в отношении 4 : 1 . Тогда можно записать, что в полученном сплаве содержится 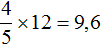
Сложим 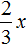
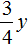
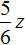
Попробуем решить данную систему.
Для начала упростим третье уравнение. Подставим в него второе уравнение и посмотрим, что из этого выйдет:
Теперь в главной системе вместо уравнения 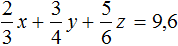
Подставим второе уравнение в первое:
Умножим первое уравнение на −10 . Тогда система примет вид:
Сложим оба уравнения. Тогда получим простейшее уравнение −5y = −4,8 откуда найдём y равный 0,96 . Значит масса второго сплава составляет 0,96 кг .
Теперь найдём x . Для этого удобно воспользоваться уравнением x = 2y. Значение y уже известно. Осталось только подставить его:
Значит масса первого сплава составляет 1,92 кг .
Теперь найдём z . Для этого удобно воспользоваться уравнением x + y + z = 12 . Значения x и y уже известны. Подставим их куда нужно:
Значит масса третьего сплава составляет 9,12 кг.
Видео:СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Задания по теме Системы уравнений
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Задания по теме Системы уравнений.7 класс

Краткое описание документа:
Задания по теме Системы уравнений.7 класс
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 691 человек из 75 регионов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 861 человек из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 51 человек из 23 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Видео:Решение систем уравнений методом сложенияСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 841 507 материалов в базе
Материал подходит для УМК
«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
§ 16. Решение систем линейных уравнений
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 22.04.2018
- 2547
- 0
- 22.04.2018
- 1216
- 24
- 22.04.2018
- 2836
- 10
- 22.04.2018
- 448
- 1
- 21.04.2018
- 562
- 2
- 21.04.2018
- 576
- 3
- 21.04.2018
- 834
- 0
- 20.04.2018
- 224
- 0
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 22.04.2018 22868
- DOCX 718.4 кбайт
- 1294 скачивания
- Рейтинг: 3 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Булдакова Любовь Петровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет и 5 месяцев
- Подписчики: 12
- Всего просмотров: 775560
- Всего материалов: 430
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Госдума рассматривает проект о регулировании «продленок» в школах
Время чтения: 1 минута
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
Минобрнауки отменило плановые и внеплановые проверки вузов в 2022 году
Время чтения: 1 минута
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
Эвакуированные в Россию из ДНР и ЛНР дети смогут поступить в вузы по квоте
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
🎥 Видео
Решение системы линейных уравнений графическим методом. Практическая часть. 7 класс.Скачать

Урок по теме СПОСОБ ПОДСТАНОВКИ 7 классСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Система с тремя переменнымиСкачать

Решение систем уравнений методом сложенияСкачать

Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Решение систем уравнений методом подстановкиСкачать

Алгебра 7 класс. 28 октября. Решаем систему уравнений методом сложения #2Скачать

Линейное уравнение с двумя переменными. 7 класс.Скачать