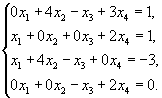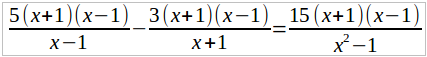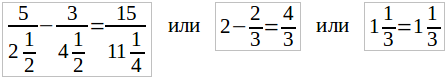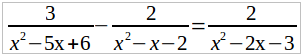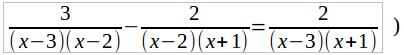Сложные математические уравнения высшей математика с ответами примеры и ответы

На этой странице мы собрали простые и сложные примеры из курса высшей математики — от векторов и матриц до дифференциальных уравнений. На каждую тему приведен один решенный пример и даны ссылки на разделы, где собраны другие решения. Фактически, это шпаргалка-каталог типовых задач и решений к ним.

Если вам нужна помощь, узнайте больше о заказе решений по высшей математике.

Далее решенные задачи по темам:

Видео:9 Математических Загадок, Которые Поставят в Тупик Даже Самых УмныхСкачать

Высшая математика. Комплексные числа

Задача. Вычислить сумму $(z_1 + z_2)$ и разность $(z_1 — z_2)$ комплексных чисел, заданных в показательной форме, переведя их в алгебраическую форму. Построить операнды и результаты на комплексной плоскости.

Видео:Мэри решает сложные примеры по математике | Одарённая (2017)Скачать

Высшая математика. Матрицы

Задача. Найти матрицу, обратную матрице $A$. Сделать проверку.

$$A= begin 1 & 2 & 1 & -1\ 1 & 1 & 0 & 0\ 0 & 2 & 0 & -1\ 1 & 1 & 1 & 0\ end $$

Видео:8 ЛОГИЧЕСКИХ ЗАГАДОК ДЛЯ САМЫХ УМНЫХ! Насколько хорошо развит твой мозг?Скачать

Высшая математика. Определители

Задача. Вычислить определитель матрицы $A$

$$A= begin 4 & 5 & 6 & 5 & 11\ 1 & 4 & 2 & 0 & 13\ 1 & 1 & 0 & -1 & 5\ 3 & 2 & 3 & 0 & 7\ 4 & 1 & 2 & 3 & 8\ end $$

Видео:Считаем в уме за секунду. #математика #арифметика #счет #ментальнаяарифметика #simplemathСкачать

Высшая математика. Системы уравнений

Задача. Исследовать на совместность и решить систему уравнений:

Видео:Решение демонстрационного варианта ЕГЭ по математике. Задача 13.1. #математика #егэ, #фипи, #экзаменСкачать

Высшая математика. Векторы

Задача. Написать разложение вектора $X$ по векторам $(a, b, c)$.

Видео:Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Аналитическая геометрия на плоскости

Задача. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Видео:таблица умножения школаСкачать

Аналитическая геометрия в пространстве

Задача. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Высшая математика. Пределы

Задача. Найти предел функции

Видео:Проверь свои знания по математике за 11 классСкачать

Высшая математика. Производные

Задача. Найти производную от следующей функции

Видео:Математика это не ИсламСкачать

Высшая математика. Исследование функции

Задача. Провести полное исследование функции и построить график.

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Высшая математика. Интегралы

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Высшая математика. Применение интегралов

Задача. Найти длину дуги кривой, заданной параметрическими уравнениями:

$$ x=3(1-cos t)cos t, quad y=3(1-cos t)sin t, quad 0leq t leq pi. $$

Высшая математика. Кратные и криволинейные интегралы

Видео:Самая сложная задача из самой сложной олимпиады [3Blue1Brown]Скачать

Высшая математика. Ряды

Задача. Исследовать сходимость числового ряда

Видео:Как умножать сложные числа? Лайфхак👌 #shortsСкачать

Высшая математика. Дифференциальные уравнения

Задача. Найти общее решение линейного дифференциального уравнения первого порядка

Видео:ЗАГАДКИ НА ЛОГИКУ. 4 из 5 НЕ ПРОЙДУТСкачать

Высшая математика. Теория вероятностей

Задача. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит 8; б) произведение числа очков не превосходит 8; в) произведение числа очков делится на 8.

Видео:Как списать на выпускном экзамене?Скачать

Математика

52. Более сложные примеры уравнений.
Пример 1 .

5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)

Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

5x + 5 – 3x + 3 = 15

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x 2 – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

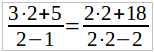
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.

Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

3x + 3 – 2x + 6 = x – 2

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

Видео:Задача из вступительного теста по математике в ОксфордСкачать

Хотите решить задачу онлайн? Получите ответ на любую задачу по математике с подробным решением за несколько секунд, например, как решить уравнение.

Видео:Олимпиадная задача пятиклассникаСкачать

Pocket Teacher искусственный интеллект, который 30 лет разрабатывали в МГУ

Видео:Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать

Получите онлайн-помощника в решении множества математических дисциплин. Решить любую задачу, например решить уравнение очень просто!

• Иррациональные
• Рациональные
• Тригонометрические
• Логарифмические
• Экспоненциальные
• С произвольными параметрами
• Показательные произвольной сложности

• Определенные
• Неопределенные

• Геометрические задачи можно вводить в текстовом виде

• Подробное решение для дифференциальных уравнений
• Системы дифференциальных уравнений

• Матрицы — посчитать определитель
• Пределы — пока без подробного решения
• Текстовые математические задачи

Видео:Прогульщик опоздал на 20-мин. и получил две ЗАДАЧИ... Его ответ поставил профессора в ступор...Скачать

Решайте задачи, заданные в текстовом виде

• Геометрии
• Физике скоро
• Химии скоро

Pocket Teacher всегда под рукой

• мобильная версия

Сервис будет полезен всем, кто сталкивается с математикой

• Проверит домашнее задание: решите задачи или уравнения и сравните результат
• Поможет разобраться в теме, которую вы пропустили или не поняли
• Поможет подготовиться к ЕГЭ

• Проверит решение ребенка
• Поможет решить задачу
• Сэкономит на репетиторе

• Поможет подготовиться к поступлению в ВУЗ и вспомнить пройденный материал
• Выручит на контрольной и экзамене
• Решит задачи из курсовой
• Сэкономит время на решении сложных задач на старших курсах
• Станет спасением для тех, у кого математика непрофильный предмет

Pocket Teacher пользуются человек

Поступил в этом году на «вышку». Ваш сайт использовал для решения вступительных примеров и тестов. Всё понравилось! Четко, быстро и правильно. Спасибо! Буду использовать ваш ресурс и дальше, но уже в работе.

Нас всё устраивает. Ошибок в решениях выявлено не было. Приятный интерфейс. Решить уравнение очень просто и быстро.

Всё отлично работает, спасибо за помощь в решении сложных заданий! Решить задачу реально очень просто!

Очень удобный и полезный сервис. Очень устраивает! Спасибо!

Я пишу студентам научные работы, и использую ваш сайт для решения задач. Своим детям также решаю задачи и сложные примеры при помощи вашего сайта. Пока все разделы и интерфейс меня полностью устраивают.

Пока испробовал не все разделы сайта, но на данный момент меня все устраивает: быстро, правильно, профессионально.

Я являюсь мамой старшеклассника, и мой сын свято верит в то, что я могу решить по математике практически всё. Поэтому ваш сайт в данном случае меня прекрасно выручает! Никаких косяков как таковых не было!

С уважением, Ольга.

Благодарю за помощь, всё работает прекрасно! Очень благодарен разработчикам за такой сервис!