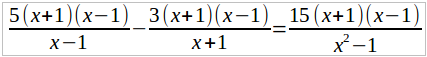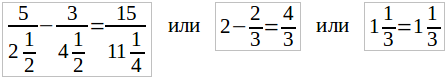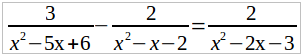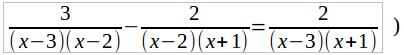Сложное уравнение с ответом 300

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Самый сложный пример чтоб получилось 300?

Математика | 1 — 4 классы

Самый сложный пример чтоб получилось 300.

(123 + 18) * 3 — (239 — 116) = 3001) 123 + 18 = 1412) 239 — 116 = 1233) 141 * 3 = 4234) 423 — 123 = 300.

Видео:Парадокс Монти Холла | Двадцать одно. 2008. Момент из фильма [1080p]Скачать

Что такое сложный пример?

Что такое сложный пример.

Видео:УРАВНЕНИЕ 4 КЛАСС МАТЕМАТИКА УЧИМСЯ РЕШАТЬ УРАВНЕНИЯ МЕТОДИКА ОБУЧЕНИЯ РЕШАЕМ УРАВНЕНИЯ #уравнениеСкачать

Задайте самую сложную сложную задачу по математике за 3 класс?

Задайте самую сложную сложную задачу по математике за 3 класс.

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Сложные примеры за 6 класс?

Сложные примеры за 6 класс.

Видео:Уборщик С 500 IQ Решил Математическую Задачу, Которая Была Не Под Силу Ни Одному ПрофессоруСкачать

Придумайте сложный пример по математике для 5 класс пж?

Придумайте сложный пример по математике для 5 класс пж.

(в примере должны быть скобки и чем пример сложнее тем лучше ).

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

СОСТАВЬТЕ ПОЖАЛУЙСТА СЛОЖНЫЙ ПРИМЕР МОЖНО ИСПОЛЬЗОВАТЬ КВАДРАТНЫЙ КОРЕНЬ , ДЛИННЫЙ?

СОСТАВЬТЕ ПОЖАЛУЙСТА СЛОЖНЫЙ ПРИМЕР МОЖНО ИСПОЛЬЗОВАТЬ КВАДРАТНЫЙ КОРЕНЬ , ДЛИННЫЙ.

ОТВЕТ ДОЛЖЕН ПОЛУЧИТЬСЯ 14, ПОЖАЛУЙСТА.

Видео:Ученик С 500 IQ Списывает На Самых Сложных Экзаменах, Даже Не ГотовясьСкачать

Помогите пожалуйста?

Можете написать мне самый сложный пример, и какое число там получилось.

РS. Можете написать пример с ответом для 11 класса.

Или для тех, кто учится в универе.

Главное чтобы сложный был.

Видео:Считаем в уме за секунду. #математика #арифметика #счет #ментальнаяарифметика #simplemathСкачать

Самый сложный пример чтобы получилось 0?

Самый сложный пример чтобы получилось 0.

Видео:Простое решение сложного уравнения ➜ Решите уравнение ➜ x⁴-2x³-13x²+14x-3=0Скачать

Пример двух сложного слова?

Пример двух сложного слова.

Видео:Как решать уравнения без применения правил?Скачать

Три примера : сложные неравенства?

Три примера : сложные неравенства.

Видео:Математика 4 класс (Урок№21 - Решение уравнений.)Скачать

Придумайте сложный пример с ответом 2?

Придумайте сложный пример с ответом 2.

На этой странице сайта, в категории Математика размещен ответ на вопрос Самый сложный пример чтоб получилось 300?. По уровню сложности вопрос рассчитан на учащихся 1 — 4 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

1025|_4 8 256 22 20 25 24 1 получается 256, и остаток 1.

Очень легко, в этом сложного ничего нет.

1) 65 * 25 = 1625 2) 1700 — 1625 = 75 руб Сдача 75 руб.

НОК (37 и 74) 74 I 2 37 I 37 37 I 37 HOK (37 и 74) = 37 * 2 = 74 НОД (37 и 74) = 37 — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — НОК (15 ; 36 : 12) 36 I 2 15 I 5 12 I 3 18 I 2 3 I 3 4 I 2 9 I..

1)60 : 5 = 12(км) — скорость велосипедиста. 2)12 + 3 = 15(км) — скорость велосипедиста. 3)60 : 15 = 4(ч) — за 4 часа велосипедист проехал. Ответ : за 4 часа проехал велосипедист со скоростью 15км / ч. Если спросят как решил 60 : 15, скажи путём п..

Привет, 1)18х + х — 12х = 18х — 11х = 7х 2) здесь обыкновенные дроби нужно перевести в десятичные 0, 6bc — 0, 5bc + 0, 3bc = 0, 6bc — 0, 2bc = 0, 4bc.

3596 — 3596 / (2314 — 2256) Решение : 1)2314 — 2256 = 58 пиши в столбик 2)3596 — 3596 = 0 3)58 / 0 = 0 Ответ : 0.

Решаем методом подбора 4 + 6 = 10 2 + 7 = 9 3 + 5 = 8.

Они симметричны. Можно измерить.

Решение : 59x — 27x = 89 32x = 89 x = 2, 78125 или дробь 2 целых 25 / 89 Ответ : 2, 78125.

Видео:Как умножать сложные числа? Лайфхак👌 #shortsСкачать

Решение сложных уравнений. 3 класс.

Овладение детьми способом решения уравнений в начальной школе создает прочную основу для дальнейшего обучения алгебры, химии, физики и других предметов.

Начиная с 3-го класса, ученикам встречаются сложные уравнения, но справиться с ними очень просто.

Дети уже умеют решать простые уравнения, читай об этом здесь.

А эта статья будет посвящена решению сложных уравнений в 2-3 действия.

Очень часто родители, желая помочь, объясняют так: вот смотри, сейчас вот это число перенести в другую часть от знака равенства, надо поменять знак на противоположный: было умножение, меняем на деление; было сложение меняем на вычитание.

В начальной школе это объяснение не срабатывает, т.к. ребенок не знаком с законами алгебры.

Как сложное уравнение привести к тому, которые мы уже умеем решать, а именно к уравнению в 1 действие?

Рассмотрим уравнение в 2 действия:

х + 56 = 98 — 2 — оно достаточно легкое.

Здесь особого труда не будет в решении, потому что ребенок сразу догадается, что сначала надо 98-2.

х + 56 = 98 — 2

х + 56 = 96 – это простое уравнение. А его решаем очень быстро!

Сейчас мы рассмотрим уравнение:

Такое уравнение можно решить несколькими способами.

1. У нас здесь неизвестное число х. Мы не знаем, что спрятано за этим числом.

А когда к х + 5 – это число тоже известно.

Закроем его и пусть это будет другое число, например b .

Мы видим, что у нас получилось самое простое уравнение в 1 действие.

2 • b = 30

А чтобы найти а, нам нужно 30 : на 2.

А b не что иное, как х + 5.

х + 5 = 30 : 2

х + 5 = 15

х = 15 – 5

х = 10

Проверку делаем как обычно: переписываем первое уравнение: 2 • (10 + 5) = 30.

30 – переписываем, а левую часть считаем — будет 30.

30 = 30, значит, уравнение решили правильно.

При решении таких сложных уравнений самое главное – понять, что заменить на другое неизвестное число. Когда в уравнении всего 2 действия – это очень просто.

1. Более удобно и понятно, как показывает практика, если использовать решение сложных уравнений на основе зависимости между компонентами действий.

Наше уравнение 2 • (х + 5) = 30 читаем так: число 2 умножить на сумму х и пяти, получится 30. В данном случае – нам неизвестна сумма, чтобы ее найти, надо 30:2.

48 : (16 – а) = 4.

Если опять заменять часть уравнения другим неизвестным числом, можно запутаться. Поэтому легче использовать взаимосвязи компонентов и результата действия: число 48 разделить на разность.

Нам неизвестна разность, поэтому сначала нужно узнать чему она равна. Надо 48 : 4.

16 — а = 48 : 4

16 — а = 12 – это простое уравнение.

а = 16 — 12

а = 4

Проверка: 48 : (16 — 4) = 4

Давайте посмотрим еще одно:

Из 96 надо вычесть разность с и 16. Чтобы найти разность, надо 96-94.

Проверка: 96 — (16 — 14) = 94

А сейчас мы переходим к тем уравнениям, у которых не 2, а 3 действия. Как же нам поступать в этом случае? При решении таких сложных уравнения используем знания порядка выполнения действий в выражениях со скобками и без них.

Рассмотрим уравнение: 36 – (8 • у + 5) = 7

Прежде всего, нужно внимательно оценить левую часть уравнения: ту, которая с неизвестным числом. Вы должны четко себе представить какое вы будете делать действие первым, какое – вторым, какое – третьим: сначала делается умножение, потом сложение и последним – вычитание.

И вот то, которое вы будете делать третьим, с него и начнем, т.е. начинаем упрощать уравнение с последнего действия. Последнее действие – вычитание. С него и начнем: из числа 36 вычесть то, что в скобках и получим 7.

Значит, то что в скобках – вычитаемое, чтобы его найти, надо 36 — 7.

По правилам математики в данной записи скобки – не ставим.

8 • у + 5 = 29 – уравнение сложное. Нужно его упростить. Данное уравнение читаем так: к произведению 8 и у прибавили 5 и получилось 29. Нам неизвестно произведение, чтобы его найти, надо 29-5.

8 • у = 24 – это уравнение простое.

Проверка: 36 — (8 • у + 5) = 7 . Правую часть – 7 — переписываем, а левую считаем.

Итак: 7 = 7. Значит, уравнение решили правильно.

(36 + d) : 4 + 8 = 18. Определяем порядок действий: первое – сложение в скобках, второе – деление, третье сложение вне скобок. Значит, все, что до 8 – это первое слагаемое, чтобы его найти, надо 18 — 8

(36 + d) : 4 = 18 — 8

(36 + d) : 4 = 10 – уравнение сложное, теперь последнее действие — :, значит

36 + d = 40 – уравнение простое и его мы решаем легко!

Для удобства и быстроты решения сложных уравнений можете пользоваться данной памяткой

Дело в том, что при кажущейся сложности, если внимательно изучить все приемы, которые я вам сегодня показала, эти уравнения дети будете щелкать как семечки. Обязательно напишите в комментариях, какой способ вам более удобен.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 58

Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Математика

52. Более сложные примеры уравнений.
Пример 1 .

5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)

Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

5x + 5 – 3x + 3 = 15

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x 2 – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

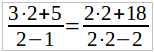
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.

Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

3x + 3 – 2x + 6 = x – 2

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

🎦 Видео

таблица умножения школаСкачать

РЕШИ ПРИМЕРЫ за 20 сек. - Выпуск 1. Тест ПО МАТЕМАТИКЕ. Взрослым не пройти. Империя ТестовСкачать

Задача, которую боятсяСкачать

НЕВОЗМОЖНОЕ УРАВНЕНИЕ | Даже не пробуйте решитьСкачать

Сложные уравнения №13 | ЕГЭ по математике | Аня МатеманяСкачать

9 Математических Загадок, Которые Поставят в Тупик Даже Самых УмныхСкачать

Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]Скачать