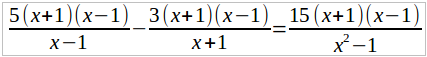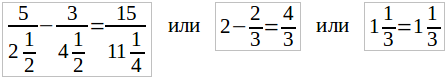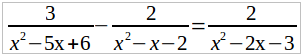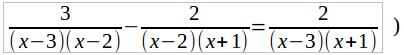52. Более сложные примеры уравнений.
Пример 1 .
5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)
Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:
или, после сокращения,
5(x + 1) – 3(x – 1) = 15
5x + 5 – 3x + 3 = 15
Рассмотрим еще уравнение:
5/(x-1) – 3/(x+1) = 4(x 2 – 1)
Видео:Сложные уравнения. Как решить сложное уравнение?Скачать
Решая, как выше, получим:
5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.
Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.
Для первого примера получим:
Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.
Для второго примера получим:
5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0
Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.
Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.
(x + 3)/(x – 1) = (2x + 3)/(2x – 2)
Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать
Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:
(x + 3) (2x – 2) = (2x + 3) (x – 1)
2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.
Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:
6x – 2x – 6 = 3x – 2x – 3
Перенесем неизвестные члены влево, известные вправо — получим:
Вспоминая данное уравнение
(x + 3)/(x – 1) = (2x + 3)/(2x – 2)
мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.
Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:
Видео:Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать
2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,
Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:
(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)
Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:
Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:
или 11 = 11
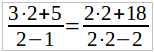
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:
(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.
Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы
Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:
1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
Если мы вспомним начальное уравнение
(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),
то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.
Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:
1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),
2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),
3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).
Общий знаменатель равен (x – 3)(x – 2)(x + 1).
Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:
на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:
Видео:Как решить сложные уравненияСкачать
3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.
Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.
Если бы мы взяли уравнение:
то, поступая совершенно так же, как выше, получили бы
3(x + 1) – 2(x – 3) = x – 2
3x + 3 – 2x + 6 = x – 2
3x – 2x – x = –3 – 6 – 2,
откуда получили бы
что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.
Сложное уравнение с ответом 10
Видео:Как решают уравнения в России и СШАСкачать
Пример 5. Решите уравнение 3у + у 2 = у.
Решение:
3у + у 2 = у – неполное квадратное уравнение; у 2 + 3у – у = 0;
у 2 + 2у =0; у∙(у + 2) = 0.
x 2 – 5х = – 6 или х 2 – 5х = 36;
х 2 – 5х + 6 = 0 или х 2 – 5х – 36 =0.
По теореме Виета:
х1 = 2, х2 = 3, х3 = – 4, х4 =9.
Ответ: – 4, 2, 3, 9.
📸 Видео
УРАВНЕНИЕ 4 КЛАСС МАТЕМАТИКА УЧИМСЯ РЕШАТЬ УРАВНЕНИЯ МЕТОДИКА ОБУЧЕНИЯ РЕШАЕМ УРАВНЕНИЯ #уравнениеСкачать
СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать
Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать
10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать
Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать
Как решать неравенства? Математика 10 класс | TutorOnlineСкачать
Как решать уравнения с дробью? #shortsСкачать
Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
СОСТАВНЫЕ УРАВНЕНИЯ / Как легко решать сложные уравнения / УРАВНЕНИЯ #математика #уравненияСкачать
Очень интересная загадка на сообразительностьСкачать
Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать
Решение тригонометрических уравнений. Практическая часть. 10 класс.Скачать
Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать
