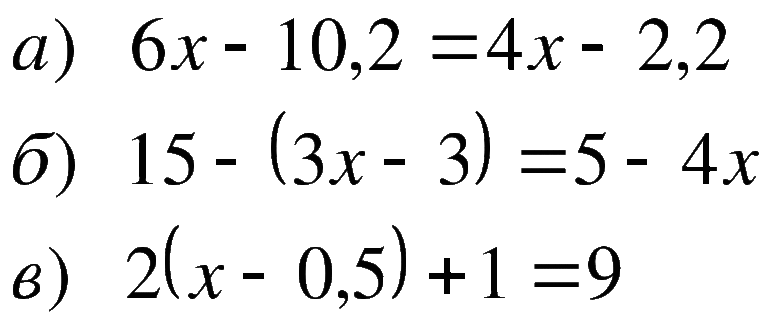Сложное уравнение 6 класс с подробным ответом

Первый вид — обыкновенные приведенные линейные уравнения, состоящие из числовых величин и переменных с единичным степенным показателем. Они являются наиболее распространенными не только в математике и физике, но и в других дисциплинах с физико-математическим уклоном. Графиком их функции является прямая линия, которую также называют прямо пропорциональной зависимостью.

Ко второму типу относятся любые многочлены линейного типа, имеющие переменную, а также некоторый параметр. Последний влияет на решение и нахождение корней. Обычно он задается на начальном этапе решения, но бывают и исключения. В последнем случае необходимо указывать диапазон допустимых значений параметра.

Суть решения второго вида уравнений — предотвратить превращение тождества в пустое множество. Для этой цели требуется исключить при помощи записи в виде неравенства все ложные значения параметра. Выражения с параметром применяются в программировании при написании и разработке различных алгоритмов. Кроме того, их можно встретить при описании физических процессов и явлений.

Последний тип — выражения высшей степени, которые при помощи математических преобразований превращаются в первый или второй тип. Для их решения необходимо знать формулы сокращенного умножения, понижающие степень до единицы, а также навык раскрытия скобок и приведения подобных компонентов.

Обыкновенные тождества

Простое линейное уравнение записывается в таком виде: At+Bt+Ct+As+Bs+Cs=0. Некоторых коэффициентов может и не быть. Кроме того, тождество может записываться в виде выражения, включающего в свой состав скобки. Алгоритм решения имеет следующий вид:

Следует отметить, что также составляются примеры линейных уравнений для тренировки в 7 классе. Необходимо разобрать решение одного из них «7 (t-1)(t+1)-7t (t-1)=8». Решать его нужно по вышеописанному алгоритму:

Последний пункт реализации методики свидетельствует о том, что корень тождества найден правильно. Далее нужно рассмотреть выражения с параметром.

Выражения с параметром

Уравнения с некоторым параметром решаются немного по другой методике. Ее суть заключается в нахождении корня, дополнительно зависящего от некоторого значения. Алгоритм имеет следующий вид:

Реализацию методики необходимо рассмотреть на практическом примере «t-2+pt=0», где р — параметр тождества. Решать выражение нужно по такому алгоритму:

Иногда в некоторых задачах нет необходимости подставлять значение параметра. В этом случае следует просто записать формулу корня, указав допустимый интервал (диапазон) последнего. Например, в вышеописанном примере решение записывается следующим образом: t=2/(1+p)

. Каждый ученик должен понять основной смысл решения уравнений этого типа — научиться находить область значений параметра, не превращающие выражение в пустое множество.

Понижение степени

Некоторые уравнения представлены степенью при неизвестной, превышающую единицу. К ним относятся следующие виды: квадратные, кубические и бикубические. Каждый из трех видов имеет собственный алгоритм нахождения корней.

Однако некоторые из них можно свести к линейному типу. Для этого применяется метод разложения на множители. Он подразумевает алгебраические соотношения, при помощи которых выражение легко записывается в обыкновенной линейной форме. К ним относятся следующие:

Первая и вторая формула называется квадратом суммы или разности соответственно. Третья — разность квадратов. Кроме того, бывают случаи, при которых невозможно применить эти тождества. Для этого требуется выносить общий множитель за скобки, тем самым понижая степень. Для нахождения корней существует определенная методика:

Реализация алгоритма нужно проверить на практическом примере, т. е. следует решить уравнение «3t^2-3=0». Найти его корни можно, воспользовавшись вышеописанной методикой:

Кубические и бикубические должны сводиться к квадратным, а затем преобразовываться в линейные, поскольку формулы кубов суммы и разности, при их разложении на множители, дают вторую степень. Однако существует еще один частный случай, о котором не упоминалось при классификации линейных выражений с неизвестными — системы уравнений.

Системы линейного типа

Система уравнений — совокупность выражений с неизвестными, которые имеют общие решения. Методика для вычисления корней имеет следующий вид:

Однако для практического применения вышеописанной методики необходимо разобрать систему уравнений, состоящую из двух тождеств (5t-2s=1 и 4t^2-s^2=0). Решать ее нужно по вышеописанной методике:

В третьем пункте математики рекомендуют разложить тождество на множители, поскольку необходимо всегда понижать степень при неизвестной величине. Во всех трех случаях описаны простые примеры, которые позволяют перейти к более сложным заданиям.

Следует отметить, что еще одним методом решения системы уравнений считается построение графиков функций, входящих в ее состав. Методика поиска решений сводится к простым шагам, которые можно править относительно предыдущего алгоритма таким образом:

В последнем пункте методики находятся корни системы уравнений. Далее рекомендуется их подставить в исходные выражения для проверки.

Таким образом, линейные уравнения применяются в различных физико-математических дисциплинах и прикладных науках. Для их решения существуют определенные методики, позволяющие выполнить эту операцию за короткий промежуток времени и не допустить ошибок.

Видео:Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Линейные уравнения — алгоритмы и примеры решений с объяснением для 6 класса

Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Общие сведения

Уравнение — совокупность чисел и переменных. Иными словами, тождеством, содержащим неизвестные величины, называется математическая запись, в которой следует определить значения переменных, превращающих это выражение в истинное. Например, переменная t в выражении 2t=6 эквивалентна 3, поскольку 2*3=6.

Линейное — тождество, в котором максимальный показатель степени при неизвестной величине всегда эквивалентен единице.

В математике существует термин «корень уравнения». Он означает, что для решения равенства необходимо найти все допустимые значения, превращающие его в истинное тождество. Далее следует разобрать классификацию линейных выражений с переменными.

Видео:Решение уравнений. Видеоурок 28. Математика 6 классСкачать

Классификация уравнений

Прежде чем рассматривать примеры уравнений по алгебре в 7 классе (изучаются подробнее, чем в 6-м), необходимо разобрать их классификацию, поскольку она влияет на алгоритм нахождения корней. Они бывают трех типов:

1. Обыкновенные.
2. С параметром.
3. Высшей степени.

Первый вид — обыкновенные приведенные линейные уравнения, состоящие из числовых величин и переменных с единичным степенным показателем. Они являются наиболее распространенными не только в математике и физике, но и в других дисциплинах с физико-математическим уклоном. Графиком их функции является прямая линия, которую также называют прямо пропорциональной зависимостью.

Ко второму типу относятся любые многочлены линейного типа, имеющие переменную, а также некоторый параметр. Последний влияет на решение и нахождение корней. Обычно он задается на начальном этапе решения, но бывают и исключения. В последнем случае необходимо указывать диапазон допустимых значений параметра.

Суть решения второго вида уравнений — предотвратить превращение тождества в пустое множество. Для этой цели требуется исключить при помощи записи в виде неравенства все ложные значения параметра. Выражения с параметром применяются в программировании при написании и разработке различных алгоритмов. Кроме того, их можно встретить при описании физических процессов и явлений.

Последний тип — выражения высшей степени, которые при помощи математических преобразований превращаются в первый или второй тип. Для их решения необходимо знать формулы сокращенного умножения, понижающие степень до единицы, а также навык раскрытия скобок и приведения подобных компонентов.

Обыкновенные тождества

Простое линейное уравнение записывается в таком виде: At+Bt+Ct+As+Bs+Cs=0. Некоторых коэффициентов может и не быть. Кроме того, тождество может записываться в виде выражения, включающего в свой состав скобки. Алгоритм решения имеет следующий вид:

1. Раскрыть скобки.
2. Произвести математические преобразования над компонентами уравнения.
3. Сгруппировать элементы: перенести неизвестные в одну, а известные — в другую сторону.
4. Найти корень или доказать его отсутствие (учитывать и знаменатель при его наличии).
5. Выполнить проверку, подставив решение в исходное равенство.

Следует отметить, что также составляются примеры линейных уравнений для тренировки в 7 классе. Необходимо разобрать решение одного из них «7 (t-1)(t+1)-7t (t-1)=8». Решать его нужно по вышеописанному алгоритму:

1. 7 (t 2 −1)-7t 2 +7t=7t 2 −7-7t 2 +7t=8.
2. 7t 2 −7t 2 +7t-7=7t-7=8.
3. 7t=15.
4. t=2,5.
5. 7 (2,5−1)(2,5+1)-7*2,5 (2,5−1)=8. При расчете можно получить следующее тождество, которое является истинным: 8=8.

Последний пункт реализации методики свидетельствует о том, что корень тождества найден правильно. Далее нужно рассмотреть выражения с параметром.

Выражения с параметром

Уравнения с некоторым параметром решаются немного по другой методике. Ее суть заключается в нахождении корня, дополнительно зависящего от некоторого значения. Алгоритм имеет следующий вид:

1. Записать равенство.
2. Раскрыть скобки и привести подобные элементы к общему виду.
3. Выполнить математические преобразования, при помощи которых следует отделить некоторый параметр от переменной.
4. Записать диапазон значений, при которых неизвестная величина в третьем пункте не превращает уравнение в пустое множество.
5. Записать формулу определения корня.
6. При необходимости подставить значение параметра.
7. Проверить результат.

Реализацию методики необходимо рассмотреть на практическом примере «t-2+pt=0», где р — параметр тождества. Решать выражение нужно по такому алгоритму:

1. t-2+pt=0.
2. Опускается, поскольку в выражении нет скобок.
3. (t+pt)=t (1+p)=2.
4. p не должен быть -1: (-inf;-1)U (-1;+inf), где -inf и +inf — минус и плюс бесконечность соответственно.
5. t=2/(1+p).
6. При p=0: t=2.
7. 2−2+0*2=0.

Иногда в некоторых задачах нет необходимости подставлять значение параметра. В этом случае следует просто записать формулу корня, указав допустимый интервал (диапазон) последнего. Например, в вышеописанном примере решение записывается следующим образом: t=2/(1+p)

. Каждый ученик должен понять основной смысл решения уравнений этого типа — научиться находить область значений параметра, не превращающие выражение в пустое множество.

Понижение степени

Некоторые уравнения представлены степенью при неизвестной, превышающую единицу. К ним относятся следующие виды: квадратные, кубические и бикубические. Каждый из трех видов имеет собственный алгоритм нахождения корней.

Однако некоторые из них можно свести к линейному типу. Для этого применяется метод разложения на множители. Он подразумевает алгебраические соотношения, при помощи которых выражение легко записывается в обыкновенной линейной форме. К ним относятся следующие:

Первая и вторая формула называется квадратом суммы или разности соответственно. Третья — разность квадратов. Кроме того, бывают случаи, при которых невозможно применить эти тождества. Для этого требуется выносить общий множитель за скобки, тем самым понижая степень. Для нахождения корней существует определенная методика:

1. Написать равенство с неизвестным.
2. Выполнить анализ его структуры и сопоставить с одним из соотношений. Если операцию выполнить невозможно, то следует осуществить математические преобразования по вынесению общего множителя.
3. Решить линейные уравнения.
4. Произвести проверку, подставив корни или корень в исходное выражение в первом пункте методики.

Реализация алгоритма нужно проверить на практическом примере, т. е. следует решить уравнение «3t^2-3=0». Найти его корни можно, воспользовавшись вышеописанной методикой:

1. 3t^2-3=0.
2. 3(t^2-1)=0.
3. Сократить обе части на 3: t^2-1=0.
4. Воспользоваться формулой сокращенного умножения (разность квадратов): (t-1)(t+1)=0.
5. У уравнения два корня: t1=1 и t2=-1.
6. Подставить t1 и t2: 3*1-3=0 и 3*(-1)^2-3=0. Оба решения являются верными, поскольку не обращают искомое тождество в пустое множество.

Кубические и бикубические должны сводиться к квадратным, а затем преобразовываться в линейные, поскольку формулы кубов суммы и разности, при их разложении на множители, дают вторую степень. Однако существует еще один частный случай, о котором не упоминалось при классификации линейных выражений с неизвестными — системы уравнений.

Системы линейного типа

Система уравнений — совокупность выражений с неизвестными, которые имеют общие решения. Методика для вычисления корней имеет следующий вид:

1. Записать систему уравнений.
2. Выбрать наиболее простое тождество и выразить одну величину через другую.
3. Подставить в любое выражение переменную, выраженную во втором пункте алгоритма.
4. Раскрыть скобки и выполнить математические преобразования.
5. Решить уравнение в четвертом пункте.
6. Подставить корень, полученный на пятом шаге алгоритма, во 2 пункт.
7. Найти вторую переменную.
8. Записать результат.
9. Выполнить проверку.

Однако для практического применения вышеописанной методики необходимо разобрать систему уравнений, состоящую из двух тождеств (5t-2s=1 и 4t^2-s^2=0). Решать ее нужно по вышеописанной методике:

1. 5t-2s=1 и 4t^2-s^2=0.
2. Простое выражение: 5t-2s=1. Выразить s: s=(5t-1)/2.
3. (2t-s)(2t+s)=[4t/2-(5t-1)/2][4t/2+(5t-1)/2]=8t=8.
4. 8t=8=>t=1.
5. 5*1-2s=1. Отсюда s=2.
6. 5*1-2*2=1=1 (равенство действительное).

В третьем пункте математики рекомендуют разложить тождество на множители, поскольку необходимо всегда понижать степень при неизвестной величине. Во всех трех случаях описаны простые примеры, которые позволяют перейти к более сложным заданиям.

Следует отметить, что еще одним методом решения системы уравнений считается построение графиков функций, входящих в ее состав. Методика поиска решений сводится к простым шагам, которые можно править относительно предыдущего алгоритма таким образом:

1. Упростить все выражения, входящие в систему.
2. Выразить одну величину через другую в каждом выражении. Следует учитывать, что искомая переменная должна быть обязательно без степени и коэффициентов.
3. Построить отдельно для каждой функции специальные таблицы значений зависимости одной переменной от другой.
4. Начертить прямоугольную систему координат.
5. Отметить точки, исходя из таблицы, в системе координат.
6. Соединить точки плавными линиями при помощи карандаша.
7. Проделать аналогичные действия над другими тождествами (5 и 6).
8. Определить точки пересечения функций и записать их координаты.

В последнем пункте методики находятся корни системы уравнений. Далее рекомендуется их подставить в исходные выражения для проверки.

Таким образом, линейные уравнения применяются в различных физико-математических дисциплинах и прикладных науках. Для их решения существуют определенные методики, позволяющие выполнить эту операцию за короткий промежуток времени и не допустить ошибок.

🌟 Видео

Сложные уравнения. Как решить сложное уравнение?Скачать

Линейное уравнение с одной переменной. 6 класс.Скачать

Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать

Решение уравнений с дробными числами в 6 классеСкачать

6 класс, 42 урок, Решение уравненийСкачать

Решить уравнение - Математика - 6 классСкачать

РЕШЕНИЕ УРАВНЕНИЙ 6 класс математика 5 классСкачать

Как решить сложные уравненияСкачать

Решение задач с помощью уравнений. Видеоурок 29. Математика 6 классСкачать

6 класс. Решение уравнений с модулями.Скачать

дробное уравнение как решать для 6 классаСкачать

Раскрытие скобок. 6 класс.Скачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать