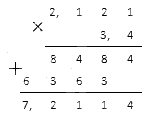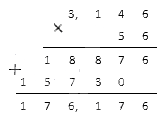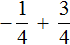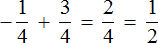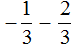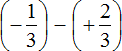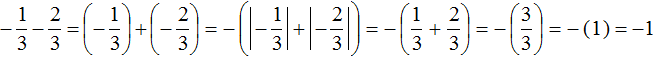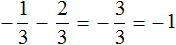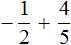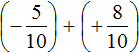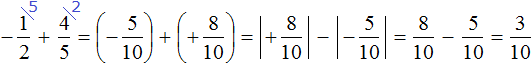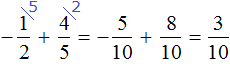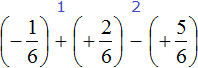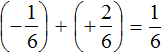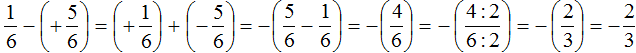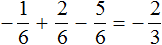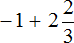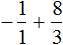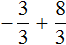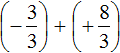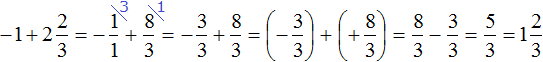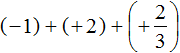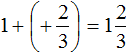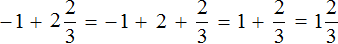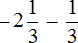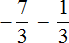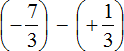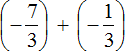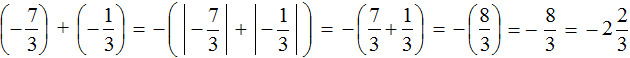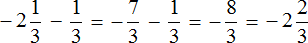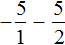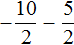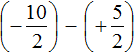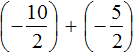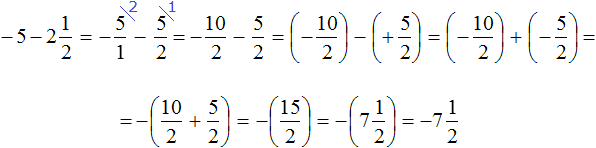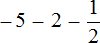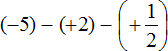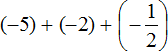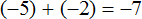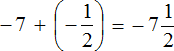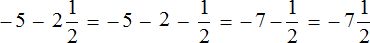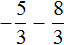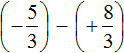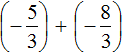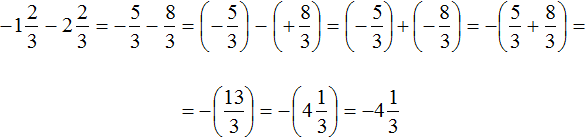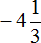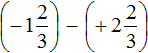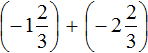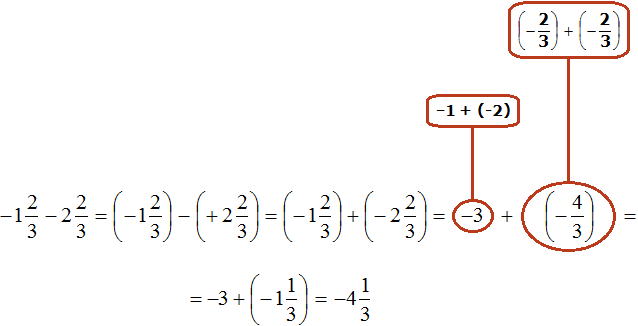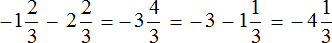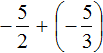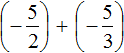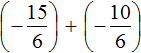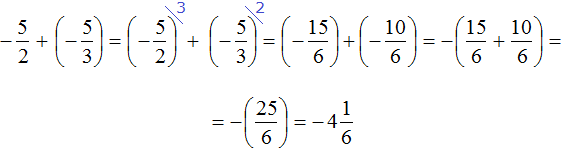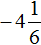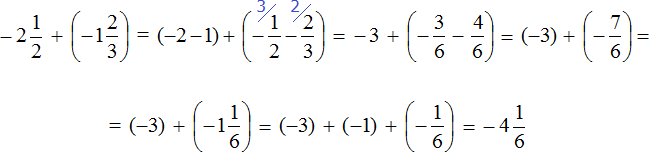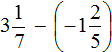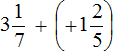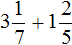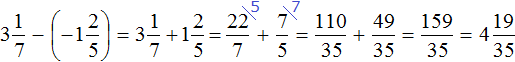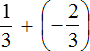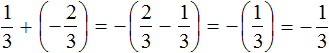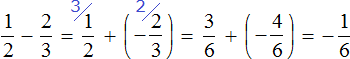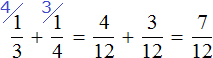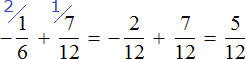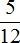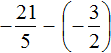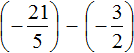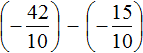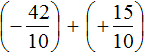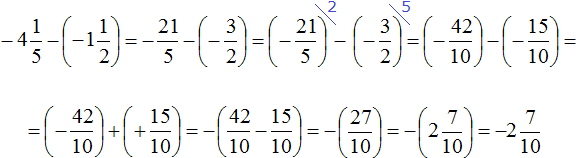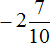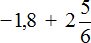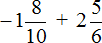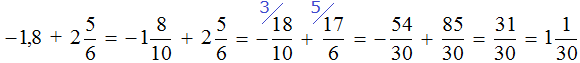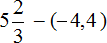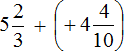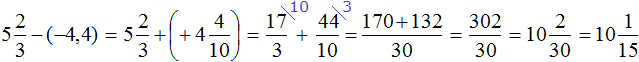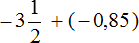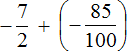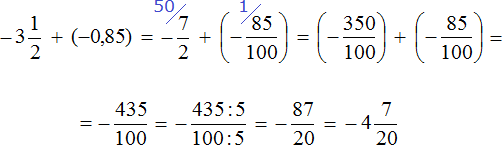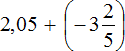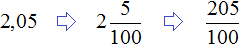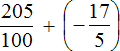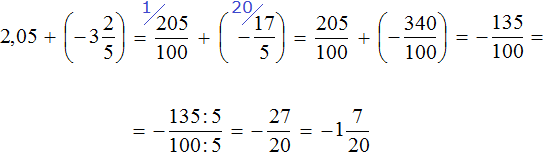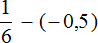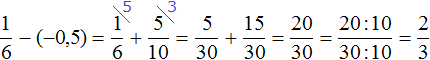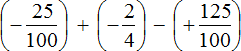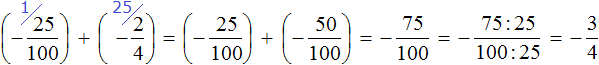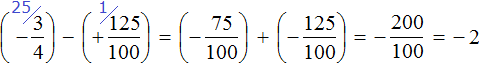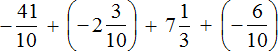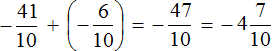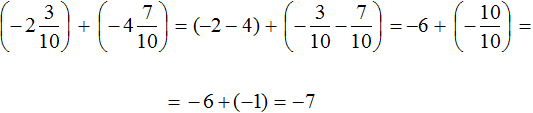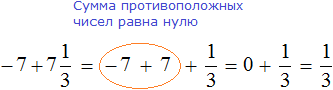Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.
- Действие сложения рациональных чисел
- Сложение нуля с отличным от него рациональным числом
- Сложение противоположных рациональных чисел
- Сложение положительных рациональных чисел
- Сложение рациональных чисел с разными знаками
- Сложение отрицательных рациональных чисел
- Действие вычитания рациональных чисел
- Действие умножения рациональных чисел
- Умножение на нуль
- Умножение на единицу
- Умножение взаимообратных чисел
- Умножение положительных рациональных чисел
- Умножение рациональных чисел с разными знаками
- Умножение отрицательных рациональных чисел
- Деление рациональных чисел
- Сложение и вычитание рациональных чисел
- Урок повторения Сложение и вычитание рациональных чисел
- Выберите документ из архива для просмотра:
- 🎬 Видео
Видео:Сложение и вычитание рациональных чисел. 6 класс.Скачать

Действие сложения рациональных чисел
Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5 + 1 4 возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.
Сформулируем правила сложения рациональных чисел:
Видео:Сложение и вычитание рациональных и отрицательных рациональных чисел. Практическая часть. 6 класс.Скачать
Сложение нуля с отличным от него рациональным числом
Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a .
Пара простых примеров: сумма рационального числа 2 , 1 и числа 0 равно 2 , 1 и: 6 4 5 + 0 = 6 4 5 .
Видео:Вычитание рациональных чисел . Решение уравнений . 6 класс .Скачать

Сложение противоположных рациональных чисел
Сумма противоположных чисел равна нулю.
Данное правило можно записать в виде: a + ( — a ) = 0 (для любого рационального числа a ).
К примеру, числа 45 , 13 и — 45 , 13 являются противоположными, т.е. их сумма равно нулю: 45 , 13 + ( — 45 , 13 ) = 0 .
Видео:Сложение и вычитание рациональных чисел. Математика 6 класс.Скачать

Сложение положительных рациональных чисел
В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.
Необходимо произвести сложение рациональных чисел: 0 , 6 и 5 9 .
Решение
Выполним перевод десятичной дроби в обыкновенную и тогда: 0 , 6 + 5 9 = 6 10 + 5 9 .
Осуществим сложение дробей с разными знаменателями:
6 10 + 5 9 = 54 90 + 50 90 = 104 90 = 1 7 45
Ответ: 0 , 6 + 5 9 = 1 7 45 .
Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.
Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Сложение рациональных чисел с разными знаками
Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.
Необходимо осуществить сложение рациональных чисел с разными знаками 8 , 2 и — 2 3 4 .
Решение
Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: | 8 , 2 | = 8 , 2 и | — 2 3 4 | = 2 3 4 . Проведя сравнение модулей — рациональных чисел, получим: 8 , 2 > 2 3 4 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8 , 2 — 2 3 4 = 8 2 10 — 2 3 4 = 5 9 20 .
Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8 , 2 + ( — 2 3 4 ) = 5 9 20 .
Видео:как ЛЕГКО сложить отрицательные числа , ПРИМЕРЫСкачать
Сложение отрицательных рациональных чисел
Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.
Необходимо произвести сложение чисел: — 4 , 0203 и — 12 , 193 .
Решение
Модули заданных чисел соответственно равны: 4 , 0203 и 12 , 193 . Сложим их:
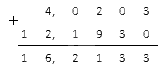
Полученному результату присваиваем знак минус: — 16 , 2133 .
Ответ: ( — 4 , 0203 ) + ( — 12 , 193 ) = — 16 , 2133 .
Видео:Вычитание рациональных чисел, 6 классСкачать

Действие вычитания рациональных чисел
Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c + b = a следует, что a — b = c и a — c = b . И наоборот: из равенств a — b = c и a — c = b следует, что c + b = a .
При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.
Необходимо вычислить разность рациональных чисел: 4 , ( 36 ) – 1 5 .
Решение
Сначала переведем периодическую десятичную дробь в обыкновенную: 4 , ( 36 ) = 4 + ( 0 , 36 + 0 , 0036 + … ) = 4 + 0 , 36 1 — 0 , 01 = 4 + 36 99 = 4 + 4 11 = 4 4 11
Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4 , ( 36 ) — 1 5 = 4 4 11 — 1 5 = 4 + 4 11 — 1 5 = 4 + 20 55 — 11 55 = 4 + 9 55 = 4 9 55
Ответ: 4 , ( 36 ) — 1 5 = 4 9 55
В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + ( — b ) .
Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: ( a + ( — b ) ) + b = a + ( ( — b ) + b ) = a + 0 = a . Отсюда в силу смысла действия вычитания следует, что сумма a + ( — b ) есть разность чисел a и b .
Необходимо из рационального числа 2 7 вычесть рациональное число 5 3 7
Решение
Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. — 5 3 7 . Тогда: 2 7 — 5 3 7 = 2 7 + — 5 3 7
Далее произведем сложение рациональных чисел с разными знаками: 2 7 + — 5 3 7 = — 5 3 7 — 2 7 = — 5 3 7 — 2 7 = — 5 1 7
Ответ: 2 7 + — 5 3 7 = — 5 1 7
Видео:Вычитание рациональных чисел. Математика 6 классСкачать

Действие умножения рациональных чисел
Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Видео:МЕРЗЛЯК-6. ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ. ПАРАГРАФ-36Скачать

Умножение на нуль
Произведение любого рационального числа a на нуль есть нуль.
Используя переместительное свойство умножения, получим: 0 · а = 0 .
К примеру, умножение рационального числа 7 13 на 0 даст 0 . Перемножив отрицательное рациональное число — 7 1 8 и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0 · 0 = 0 .
Видео:Сложение и вычитание рациональных чисел 6-класс • +как решать задания!)Скачать

Умножение на единицу
Умножение любого рационального числа a на 1 дает число a .
Т.е. a · 1 = a или 1 · a = a (для любого рационального a ). Единица здесь является нейтральным числом по умножению.
К примеру, умножение рационального числа 5 , 46 на 1 даст в итоге число 5 , 46 .
Видео:Решение уравнений, 6 классСкачать

Умножение взаимообратных чисел
Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а · а — 1 = 1 .
К примеру, результатом произведения чисел 5 6 и 6 5 будет единица.
Видео:Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравненияСкачать

Умножение положительных рациональных чисел
В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.
Необходимо вычислить произведение положительных рациональных чисел 0 , 5 и 6 25 .
Решение
Представим заданную десятичную дробь в виде обыкновенной 0 , 5 = 5 10 = 1 2 .
Далее произведем умножение обыкновенных дробей: 1 2 · 6 25 = 6 50 = 3 25 .
Ответ: 0 , 5 · 6 25 = 3 25
Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.
Необходимо вычислить произведение рациональных чисел 2 , 121 и 3 , 4 .
Решение
Перемножим десятичные дроби столбиком:
Ответ: 2 , 121 · 3 , 4 = 7 , 2114
В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.
Видео:Умножение рациональных чисел. 6 класс.Скачать

Умножение рациональных чисел с разными знаками
Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.
Необходимо найти произведение чисел: — 3 3 8 и 2 1 2
Решение
Согласно вышеуказанному правилу получим: — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2
Заменим смешанные дроби неправильными и найдем искомое произведение: — 3 3 8 · 2 1 2 = — 27 8 · 5 2 = — 135 16 = — 8 7 16
Ответ: — 3 3 8 · 2 1 2 = — 8 7 16
Видео:Деление рациональных чисел. 6 класс.Скачать
Умножение отрицательных рациональных чисел
Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.
Необходимо найти произведение отрицательных рациональных чисел — 3 , 146 и — 56 .
Решение: модули заданных чисел соответственно равны 3 , 146 и 56 .
Перемножим их столбиком:
Полученный результат и будет являться искомым произведением.
Ответ: ( — 3 , 146 ) · ( — 56 ) = 176 , 176
Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Деление рациональных чисел
Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b · c = a следует, что a : b = c и a : c = b . И наоборот: из равенств a : b = c и a : c = b следует, что b · c = a .
На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.
Разделить число а на число b , отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a : b = a · b — 1 .
Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств ( a · b — 1 ) · b = a · ( b — 1 · b ) = a · 1 = a , которая и доказывает равенство a : b = a · b — 1 .
Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.
Необходимо выполнить действие деления 3 1 3 : — 1 1 6
Решение
Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: — 1 1 6 = — 7 6 .
Число, обратное этой дроби, будет: — 6 7 . Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 3 1 3 — 1 1 6 = 3 1 3 · — 6 7 = 10 3 · ( — 6 7 ) = — ( 10 3 · 6 7 ) = — 20 7 = — 2 6 7
Ответ: 3 1 3 : — 1 1 6 = — 2 6 7
Видео:Решение уравнений с отрицательными числами.Скачать

Сложение и вычитание рациональных чисел
В данном уроке рассматривается сложение и вычитание рациональных чисел. Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.
Правила сложения и вычитания целых чисел справедливы и для рациональных чисел. Напомним, что рациональными называют числа, которые могут быть представлены в виде дроби , где a – это числитель дроби, b – знаменатель дроби. При этом, b не должно быть нулём.
В данном уроке дроби и смешанные числа мы всё чаще будем называть одним общим словосочетанием — рациональные числа.
Пример 1. Найти значение выражения:
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:
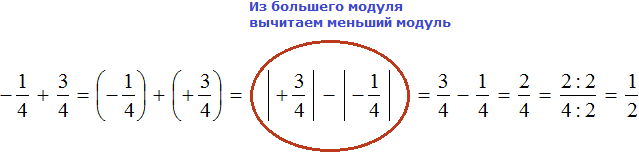
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:
Модуль рационального числа больше, чем модуль рационального числа . Поэтому мы из вычли 

Некоторые примитивные действия, такие как заключение чисел в скобки и проставление модулей, можно пропустить. Данный пример вполне можно записать покороче:
Пример 2. Найти значение выражения:
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус, стоящий между рациональными числами 
Заменим вычитание сложением. Напомним, что для этого нужно к уменьшаемому прибавить число, противоположное вычитаемому:
Получили сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Запишем решение данного примера покороче:
Примечание. Заключать в скобки каждое рациональное число вовсе необязательно. Делается это для удобства, чтобы хорошо видеть какие знаки имеют рациональные числа.
Пример 3. Найти значение выражения:
В этом выражении у дробей разные знаменатели. Чтобы облегчить себе задачу, приведём эти дроби к общему знаменателю. Не будем подробно останавливаться на том как это сделать. Если испытываете с этим затруднения, обязательно повторите урок действия с дробями.
После приведения дробей к общему знаменателю выражение примет следующий вид:
Заключим каждое рациональное число в скобки вместе своими знаками:
Это сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:
Запишем решение данного примера покороче:
Пример 4. Найти значение выражения
Заключим каждое рациональное число в скобки вместе со своими знаками:
Вычислим данное выражение в следующем порядке: слóжим рациональные числа 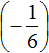
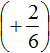
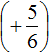
Первое действие:
Второе действие:
Таким образом, значение выражения равно
Пример 5. Найти значение выражения:
Представим целое число −1 в виде дроби 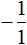

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Получили сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:
Есть и второй способ решения. Он заключается в том, чтобы сложить отдельно целые части.
Итак, вернёмся к изначальному выражению:
Заключим каждое число в скобки. Для этого смешанное число 
Вычислим целые части:
В главном выражении вместо (−1) + (+2) запишем полученную единицу:
Полученное выражение 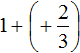
Запишем решение этим способом покороче:
Пример 6. Найти значение выражения
Переведём смешанное число 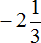
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Запишем решение данного примера покороче:
Пример 7. Найти значение выражение
Представим целое число −5 в виде дроби 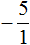

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения 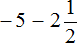
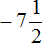
Решим данный пример вторым способом. Вернемся к изначальному выражению:
Запишем смешанное число 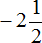
Заключим каждое рациональное число в скобки вместе своими знаками:
Заменим вычитание сложением там, где это можно:
Вычислим целые части:
В главном выражении вместо 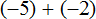
Выражение 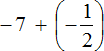
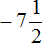

Запишем это решение покороче:
Пример 8. Найти значение выражения
Переведём смешанные числа в неправильные дроби:
Заключим каждое рациональное число в скобки вместе своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения равно
Данный пример можно решить и вторым способом. Он заключается в том, чтобы сложить целые и дробные части по отдельности. Вернёмся к изначальному выражению:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус. Но в этот раз слóжим по отдельности целые части (−1 и −2), и дробные 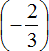
Запишем это решение покороче:
Пример 9. Найти выражения выражения
Переведём смешанные числа в неправильные дроби:
Заключим рациональное число 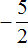
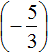
Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения 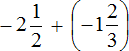
Теперь попробуем решить этот же пример вторым способом, а именно сложением целых и дробных частей по отдельности.
В этот раз, в целях получения короткого решения, попробуем пропустить некоторые действия, такие как: запись смешанного числа в развёрнутом виде и замена вычитания сложением:
Обратите внимание, что дробные части были приведены к общему знаменателю.
Пример 10. Найти значение выражения
Заменим вычитание сложением:
В получившемся выражении нет отрицательных чисел, которые являются основной причиной допущения ошибок. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вычитаемым, а также убрать скобки:
Получилось простейшее выражение, которое вычисляется легко. Вычислим его любым удобным для нас способом:
Пример 11. Найти значение выражения
Это сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Пример 12. Найти значение выражения
Выражение состоит из нескольких рациональных чисел. Согласно порядку действий, в первую очередь необходимо выполнить действия в скобках.
Сначала вычислим выражение 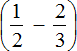
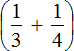
Первое действие:
Второе действие:
Третье действие:
Ответ: значение выражения 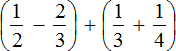
Пример 13. Найти значение выражения
Переведём смешанные числа в неправильные дроби:
Заключим рациональное число 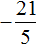
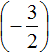
Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заменим вычитание сложением:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Таким образом, значение выражения 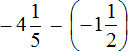
Рассмотрим сложение и вычитание десятичных дробей, которые тоже относятся к рациональным числам и которые могут быть как положительными, так и отрицательными.
Пример 14. Найти значение выражения −3,2 + 4,3
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к десятичной дроби 4,3. У этой десятичной дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы его запишем для наглядности:
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:
Модуль числа 4,3 больше, чем модуль числа −3,2 поэтому мы из 4,3 вычли 3,2. Получили ответ 1,1. Ответ положителен, поскольку перед ответом должен стоять знак того рационального числа, модуль которого больше. А модуль числа 4,3 больше, чем модуль числа −3,2
Таким образом, значение выражения −3,2 + (+4,3) равно 1,1
Этот пример можно записать покороче:
Пример 15. Найти значение выражения 3,5 + (−8,3)
Это сложение рациональных чисел с разными знаками. Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим знак того рационального числа, модуль которого больше:
3,5 + (−8,3) = −(|−8,3| − |3,5|) = −(8,3 − 3,5) = −(4,8) = −4,8
Таким образом, значение выражения 3,5 + (−8,3) равно −4,8
Этот пример можно записать покороче:
Пример 16. Найти значение выражения −7,2 + (−3,11)
Это сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус.
Запись с модулями можно пропустить, чтобы не загромождать выражение:
−7,2 + (−3,11) = −7,20 + (−3,11) = −(7,20 + 3,11) = −(10,31) = −10,31
Таким образом, значение выражения −7,2 + (−3,11) равно −10,31
Этот пример можно записать покороче:
Пример 17. Найти значение выражения −0,48 + (−2,7)
Это сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
−0,48 + (−2,7) = (−0,48) + (−2,70) = −(0,48 + 2,70) = −(3,18) = −3,18
Пример 18. Найти значение выражения −4,9 − 5,9
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который располагается между рациональными числами −4,9 и 5,9 является знаком операции и не относится к числу 5,9. У этого рационального числа свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:
(−4,9) + (−5,9) = −(4,9 + 5,9) = −(10,8) = −10,8
Таким образом, значение выражения −4,9 − 5,9 равно −10,8
Запишем решение этого примера покороче:
Пример 19. Найти значение выражения 7 − 9,3
Заключим в скобки каждое число вместе со своими знаками
Заменим вычитание сложением
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:
(+7) + (−9,3) = −(9,3 − 7) = −(2,3) = −2,3
Таким образом, значение выражения 7 − 9,3 равно −2,3
Запишем решение этого примера покороче:
Пример 20. Найти значение выражения −0,25 − (−1,2)
Заменим вычитание сложением:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:
−0,25 + (+1,2) = 1,2 − 0,25 = 0,95
Запишем решение этого примера покороче:
Пример 21. Найти значение выражения −3,5 + (4,1 − 7,1)
Выполним действия в скобках, затем слóжим полученный ответ с числом −3,5
Первое действие:
4,1 − 7,1 = (+4,1) − (+7,1) = (+4,1) + (−7,1) = −(7,1 − 4,1) = −(3,0) = −3,0
Второе действие:
−3,5 + (−3,0) = −(3,5 + 3,0) = −(6,5) = −6,5
Ответ: значение выражения −3,5 + (4,1 − 7,1) равно −6,5.
Пример 22. Найти значение выражения (3,5 − 2,9) − (3,7 − 9,1)
Выполним действия в скобках. Затем из числа, которое получилось в результате выполнения первых скобок, вычтем число, которое получилось в результате выполнения вторых скобок:
Первое действие:
3,5 − 2,9 = (+3,5) − (+2,9) = (+3,5) + (−2,9) = 3,5 − 2,9 = 0,6
Второе действие:
3,7 − 9,1 = (+3,7) − (+9,1) = (+3,7) + (−9,1) = −(9,1 − 3,7) = −(5,4) = −5,4
Третье действие
0,6 − (−5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6
Ответ: значение выражения (3,5 − 2,9) − (3,7 − 9,1) равно 6.
Пример 23. Найти значение выражения −3,8 + 17,15 − 6,2 − 6,15
Заключим в скобки каждое рациональное число вместе со своими знаками
Заменим вычитание сложением там, где это можно:
Выражение состоит из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.
Не будем изобретать велосипед, а слóжим все слагаемые слева направо в порядке их следования:
Первое действие:
(−3,8) + (+17,15) = 17,15 − 3,80 = 13,35
Второе действие:
13,35 + (−6,2) = 13,35 − 6,20 = 7,15
Третье действие:
7,15 + (−6,15) = 7,15 − 6,15 = 1,00 = 1
Ответ: значение выражения −3,8 + 17,15 − 6,2 − 6,15 равно 1.
Пример 24. Найти значение выражения
Переведём десятичную дробь −1,8 в смешанное число. Остальное перепишем без изменения:
Далее вычисляем данное выражение, применяя ранее изученные правила:
Пример 25. Найти значение выражения
Заменим вычитание сложением. Попутно переведём десятичную дробь (−4,4) в неправильную дробь
В получившемся выражении нет отрицательных чисел. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и убрать скобки. Тогда получим простое выражение на сложение, которое решается легко
Пример 26. Найти значение выражения
Переведём смешанное число 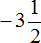
Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:
Пример 27. Найти значение выражения
Переведём обе дроби в неправильные дроби. Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:
После перевода обеих дробей в неправильные дроби, получим следующее выражение:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль и перед полученным ответом поставим знак того числа, модуль которого больше:
Пример 28. Найти значение выражения
Заменим вычитание сложением. Далее переведём десятичную дробь в обыкновенную дробь. Затем вычислим получившееся выражение, применяя ранее изученные правила:
Пример 29. Найти значение выражения
Переведём десятичные дроби −0,25 и −1,25 в обыкновенные дроби, остальное перепишем без изменения. Получим следующее выражение:
Можно сначала заменить вычитание сложением там, где это можно и сложить рациональные числа одно за другим.
Есть и второй вариант: сначала сложить рациональные числа 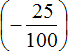
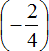
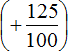
Первое действие:
Второе действие:
Ответ: значение выражения 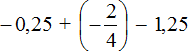
Пример 30. Найти значение выражения
Переведём десятичные дроби в обыкновенные. Остальное перепишем без изменения:
Получили сумму из нескольких слагаемых. Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.
Поэтому мы можем организовать наиболее удобный для нас вариант. В первую очередь можно сложить первое и последнее слагаемое, а именно рациональные числа 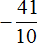
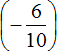
Первое действие:
Полученное число можно сложить со вторым слагаемым, а именно с рациональным числом 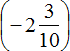
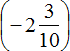
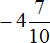
Второе действие:
Ну и слóжим полученное число −7 с последним слагаемым, а именно с рациональным числом 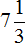
Третье действие:
Ответ: значение выражения 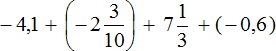
Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Урок повторения Сложение и вычитание рациональных чисел
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Мой урок.docx
План-конспект урока по математике в 6 классе.
Тема урока «Сложение и вычитание рациональных чисел».
Тип урока : урок закрепления и обобщения полученных знаний.
Цель урока : повторение ранее пройденного материала, выработать навык в сложении и вычитании рациональных чисел, отработка счетных навыков.
усвоение и закрепление учащимися знаний по теме: «Сложение и вычитание рациональных чисел»;
формировать умение применять математические знания к решению практических задач;
систематизировать знания и умения, полученные на прошлых уроках;
проверить способность учащихся самостоятельно справляться с заданием;
содействовать развитию прочных знаний, самостоятельно добытых учащимися;
развивать познавательную активность;
формировать логическое мышление.
воспитывать культуру речи;
воспитывать интерес к предмету.
Оборудование: компьютер, мультимедийный проектор.
Технологии: обучение в сотрудничестве, ИКТ, уровневая дифференциация.
1. Организация начала урока.
Приветствие учащихся проверка готовности к уроку.
2. Актуализация знаний
«Математическое лото» — работа в группах. Собрав лото прочитайте слово.
Тема нашего урока «Повторение». А что должны повторить мы сегодня на уроке?
3. Мотивация урока
+ Сложение и вычитание рациональных чисел
Какие цели и задачи поставим на сегодняшний урок
Открываем тетради записываем число и тему урока ( СЛАЙД 1)
Ребята рациональные числа появились очень давно. О таких числах математики знали ещё 2000 лет назад. Для производства вычислений математики того времени пользовались счётной доской, на которой числа изображались с помощью счётных палочек. Так как знаков «+» и «-» в то время не было, палочки красного цвета изображали положительные числа, отрицательные же — палочками чёрного цвета. Отрицательные числа долгое время называли словами, которые означали «долг», «недостача». В 7 веке в Индии положительные числа толковали как платёж, имущество, а отрицательные – как долг.
Вот как в рукописях того времени излагались правила: (СЛАЙД 2)
сумма двух имуществ есть имущество;
сумма двух долгов есть долг;
сумма нуля и долга есть долг;
сумма имуществ и нуля есть имущество.
Переведите эти высказывания на современный язык.
4.Работа по теме урока
Решаем устно «Запусти шар в небо» (СЛАЙД 3 – 8)
Учитель математики предложил шестиклассникам решить это задание дома. Как обычно, Витя Верхоглядкин сел за выполнение домашнего задания. Однако дело шло очень медленно. Тогда ему на помощь пришли мама, папа и бабушка. Они выполняли все действия по порядку, пока от усталости не стали смыкаться глаза. Наконец-то, сумма была найдена. На следующий день, во время завтрака, вся семья ругала неразумного учителя, задающего детям такие объемные задания. (СЛАЙД 9)
– А, вы, ребята, как бы решили задание, т.е. нашли значение следующего выражения:
– 499 + (– 498) + (– 497) + …+ 497 + 498+ 499 + 500 + 501?
Ребята, а какие правила не выучил Витя?
+Сложение противоположных чисел, переместительное свойство сложения
А для вас новое задание: (обсуждаем решение в парах)
Сколько целых чисел расположено на координатной прямой между числами – 34 и 36? Чему равна их сумма? (СЛАЙД 10)
+ 33 отрицательных числа, 35 положительных и ноль. Всего 69 чисел.
Их сумма равна 35 + 36 = 71. Все остальные числа являются противоположными и в сумме дают ноль.
Работа в парах (СЛАЙД 11,12)
Из данных чисел выберите любые два – 93,4 и 104,25; – 51,3 и – 78,39; 29,1 и – 87,34 и с соседом по парте выполните задания:
1) сравните эти числа,
2) найдите сумму,
3) найдите разность,
4) найдите сумму модулей этих чисел.
— 93,4 + 104,25 = 10,85
— 93,4 — 104,25 = — 197,65
|— 93,4|+ |104,25|= 197,65
— 51,3 + (— 78,39) = — 129,69
— 51,3 — ( — 78,39) = 27,09
|— 51,3|+ |— 78,39|= 129,69
29,1 + (— 87,34) = — 58,24
29,1 — ( — 87,34) = 116,44
|29,1|+ |— 87,34|= 116,44
Все мы знаем, что математика нам необходима в жизни, где в нашей жизни мы можем встретить отрицательные числа? Какой школьный предмет также связан с положительными и отрицательными числами?
Сейчас мы с вами решим несколько задач, которые ещё раз подтвердят нам этот факт.
№ 999 (В воде мертвого моря содержится около 32% соли) (СЛАЙД 13)
ФИЗКУЛЬТМИНУТКА (СЛАЙД 14)
Учащимся предлагается определить верно или нет утверждение: если согласен «присесть», если нет «встать»
1. Сумма отрицательных чисел всегда отрицательна (да)
2. Сумма двух чисел с разными знаками всегда положительна (нет)
3. Сумма противоположных чисел равна нулю (да)
4. Сумма двух отрицательных чисел может быть положительной (нет)
5. Сумма двух отрицательных чисел может быть равна нулю (нет)
Согласен «руки на пояс» не согласен «руки вверх»
6. Вычитание рациональных чисел может быть заменено на сложение с противоположным числом (да)
7. Модуль может быть отрицательным числом (нет)
8. Два числа, отличающиеся друг от друга только знаками, называются противоположными числами (да)
9. Разность двух чисел положительна, верно ли что первое число меньше второго? (нет)
Упражнения на внимание (работа с интерактивной доской)
1. «Найди ошибку при решении уравнений»
— Какие правила были нарушены?
2. Упростить выражение: (СЛАЙД 15)
8,19 + а + ( — 5,8) + ( — 3,19) + 5,8 и найдите его значение при а = — 2
Кто выполнит первый, объясняет свои действия и читает правила, которые использовались при решении.
3. Не выполняя вычисления, сравните: (СЛАЙД 16)
1) сумму чисел -6,78 и — 9,24 и их разность
2) сумму чисел -25 и 43 и сумму -95 и 88
Работа разноуровневая. Задания 1 части оцениваются в 1 балл, задания второй части – 2 балла, третьей части – 3 балла.
🎬 Видео
Сложение и вычитание отрицательных чисел.Скачать

Сложение рациональных чисел, 6 классСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать