Уравнения Максвелла для электромагнитного поля — основные законы электродинамики
Система уравнений Максвелла обязана своим названием и появлением Джеймсу Клерку Максвеллу, сформулировавшему и записавшему данные уравнения в конце 19 века.
Максвелл Джемс Кларк (1831 — 1879) был известным британским физиком и математиком, профессором Кембриджского университета в Англии.
Он практически объединил в своих уравнениях все накопленные к тому времени экспериментально полученные результаты касательно электричества и магнетизма и придал законам электромагнетизма четкую математическую форму. Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году.
Максвелл развил учение Фарадея об электромагнитном поле в стройную математическую теорию, из которой вытекала возможность волнового распространения электромагнитных процессов. При этом оказалось, что скорость распространения электромагнитных процессов равна скорости света (величина которой была уже известна из опытов).
Это совпадение послужило для Максвелла основанием к тому, чтобы высказать идею об общей природе электромагнитных и световых явлений, т.е. об электромагнитной природе света.
Созданная Джеймсом Максвеллом теория электромагнитных явлений нашла первое подтверждение в опытах Герца, впервые получившего электромагнитные волны.
В итоге эти уравнения сыграли главную роль в формировании точных представлений классической электродинамики. Уравнения Максвелла могут быть записаны в дифференциальной или интегральной форме. Практически они описывают сухим языком математики электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и в сплошных средах. К данным уравнениям можно добавить выражение для силы Лоренца, в этом случае мы получим полную систему уравнений классической электродинамики.
Чтобы понимать некоторые математические символы, использующиеся в дифференциальных формах уравнений Максвелла, для начала определим такую занятную вещь, как оператор набла.
Оператор набла (или оператор Гамильтона) — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Для нашего реального пространства, которое является трехмерным, адекватна прямоугольная система координат, для которой оператор набла определяется следующим образом:
где i, j и k – единичные координатные векторы
Оператор набла, будучи применен к полю тем или иным математическим образом, дает три возможные комбинации. Данные комбинации именуются:
Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.
Дивергенция (расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.
Ротор (вихрь, ротация) — векторный дифференциальный оператор над векторным полем.
Теперь рассмотрим непосредственно уравнения Максвелла в интегральной (слева) и дифференциальной (справа) формах, содержащие в себе основные законы электрического и магнитного полей, включая электромагнитную индукцию.
Интегральная форма: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.
Дифференциальная форма: при всяком изменении магнитного поля возникает вихревое электрическое поле, пропорциональное скорости изменения индукции магнитного поля.
Физический смысл: всякое изменение магнитного поля во времени вызывает появление вихревого электрического поля.
Интегральная форма: поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю. Это означает, что в природе нет магнитных зарядов.
Дифференциальная форма: поток силовых линий индукции магнитного поля из бесконечного элементарного объёма равен нулю, так как поле вихревое.
Физический смысл: источники магнитного поля в виде магнитных зарядов в природе отсутствуют.
Интегральная форма: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром.
Дифференциальная форма: вокруг любого проводника с током и вокруг любого переменного электрического поля существует вихревое магнитное поле.
Физический смысл: протекание тока проводимости по проводникам и изменения электрического поля во времени приводят к появлению вихревого магнитного поля.
Интегральная форма: поток вектора электростатической индукции через произвольную замкнутую поверхность, охватывающую заряды, прямо пропорционален суммарному заряду, расположенному внутри этой поверхности.
Дифференциальная форма: поток вектора индукции электростатического поля из бесконечного элементарного объема прямо пропорционален суммарному заряду, находящемуся в этом объёме.
Физический смысл: источником электрического поля является электрический заряд.
Система данных уравнений может быть дополнена системой так называемых материальных уравнений, которые характеризуют свойства заполняющей пространство материальной среды:
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Не пропустите обновления, подпишитесь на наши соцсети:
Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Уравнения Максвелла для электромагнитного поля
Введение Максвеллом понятия тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.
В основе теории Максвелла лежат рассмотренные выше четыре уравнения:
1. Электрическое поле может быть как потенциальным (ЕQ), так и вихревым (ЕB), поэтому напряженность суммарного поля Е=ЕQ +ЕB. Так как циркуляция вектора ЕQ равна нулю (см. (137.3)), а циркуляция вектора ЕB определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса для поля D (см. (89.3)):
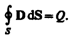
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, то формула (139.1) запишется в виде
4. Теорема Гаусса для поля В (см. (120.3)):
Итак, полная система уравнений Максвелла в интегральной форме:
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):
где e0 и m0 — соответственно электрическая и магнитная постоянные, e и m — соответственно диэлектрическая и магнитная проницаемости, g — удельная проводимость вещества.
Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид
т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.
Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса
можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.
Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше:
(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).
Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.
Теория Максвелла, являясь обобщением основных законов электрических и магнитных явлений, не только смогла объяснить уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения, что позволило Максвеллу предсказать существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме равна скорости света с = 3×10 8 м/с. Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны. Электромагнитные волны на опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что законы их возбуждения и распространения полностью описываются уравнениями Максвелла. Таким образом, теория Максвелла была экспериментально подтверждена.
К электромагнитному полю применим только принцип относительности Эйнштейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью с не совместим с принципом относительности Галилея.
Согласно принципу относительности Эйнштейна, механические, оптические и электромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла инвариантны относительно преобразований Лоренца: их вид не меняется при переходе от одной инерциальной системы отсчета к другой, хотя величины Е, В, D, Н в них преобразуются по определенным правилам.
Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Taк, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле.
Таким образом, теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, базирующейся на представлении об электромагнитном поле.
Ток смещения
Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.
Рассмотрим цепь переменного тока, содержащую конденсатор (рис. 196). Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор «протекают» токи смещения, причем в тех участках, где отсутствуют проводники.
Найдем количественную связь между изменяющимся электрическим и вызываемым им магнитным полями. По Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обкладками конденсатора существовал ток смещения, равный току в подводящих проводах. Тогда можно утверждать, что токи проводимости (I) и смещения (Iсм) равны: Iсм =I.
Ток проводимости вблизи обкладок конденсатора
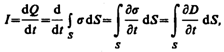
(поверхностная плотность заряда s на обкладках равна электрическому смещению D в конденсаторе (см. (92.1)). Подынтегральное выражение в (138.1) можно рассматривать как частный случай скалярного произведения 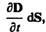

Сравнивая это выражение с 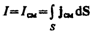

Выражение (138.2) и было названо Максвеллом плотностью тока смещения.
Рассмотрим, каково же направление векторов плотностей токов проводимости и смещения j и jсм. При зарядке конденсатора (рис. 197, а) через проводник, соединяющий обкладки, ток течет от правой обкладки к левой; поле в конденсаторе усиливается; следовательно, 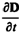
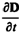
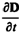
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.
ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры.
ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Система уравнений Максвелла для электромагнитного поля
Читайте также:
|

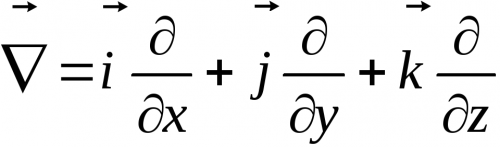
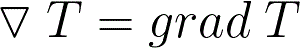
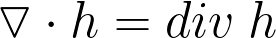
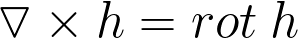
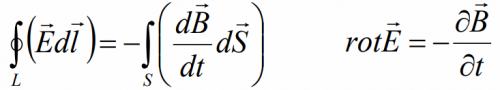
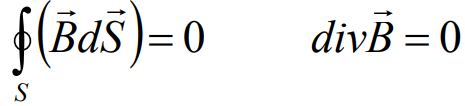
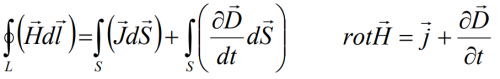
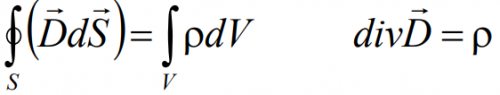
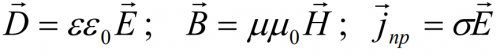



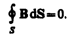


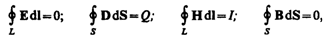

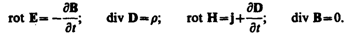








 этого поля
этого поля
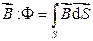 откуда следует
откуда следует 
 не равна нулю, т.е.
не равна нулю, т.е. , возбуждаемое переменным магнитным полем, как и само магнитное поле, является вихревым.
, возбуждаемое переменным магнитным полем, как и само магнитное поле, является вихревым.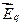 и вихревого электрического поля
и вихревого электрического поля  равна нулю, то циркуляция суммарного поля
равна нулю, то циркуляция суммарного поля
 Плотность тока смещения
Плотность тока смещения
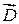 , но не самим вектором
, но не самим вектором 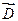 . Так, например, в поле плоского конденсатора вектор
. Так, например, в поле плоского конденсатора вектор  , а следовательно и ток смещения направлены так, как показано на рисунке (а). Если же электрическое поле убывает, то
, а следовательно и ток смещения направлены так, как показано на рисунке (а). Если же электрическое поле убывает, то  направлено от отрицательной пластины к положительной, и магнитное поле противоположно (рис. (б)) по сравнению с первым случаем.
направлено от отрицательной пластины к положительной, и магнитное поле противоположно (рис. (б)) по сравнению с первым случаем.
 , использовав полный ток
, использовав полный ток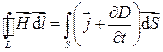
 представляет собой второе уравнение системы уравнений Максвелла для электромагнитного поля.
представляет собой второе уравнение системы уравнений Максвелла для электромагнитного поля. Для заряда, непрерывно
Для заряда, непрерывно





 ,
, 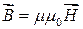 ,
, 



 в данной точке М называют следующие производные по объёму
в данной точке М называют следующие производные по объёму  ,
, 
 и
и  есть, соответственно, скалярный и векторный потоки векторного поля через замкнутую поверхность S, которая окружает данную точку М , охватывая область с объёмом V.
есть, соответственно, скалярный и векторный потоки векторного поля через замкнутую поверхность S, которая окружает данную точку М , охватывая область с объёмом V.



 явно демонстрирует, что источниками
явно демонстрирует, что источниками отражает
отражает
















