Изучение курса сопротивления материалов (наука о прочности, жесткости и устойчивости деформируемых под нагрузкой элементов машин и конструкций) следует начать с повторения раздела «Статика» (равновесие тел, уравнения равновесия, геометрические характеристики сечений). Непременными условиями успешного овладения учебным материалом являются: а) четкое понимание физического смысла рассматриваемых понятий; б) свободное владение методом сечений; в) осознанное применение геометрических характеристик прочности и жесткости поперечных сечений; г) самостоятельное решение достаточно большого числа задач. Принципиальная схема изучения каждого из видов нагружения бруса (старый термин «вид деформации») единообразна: от внешних сил с помощью метода сечения к внутренним силовым факторам, от них — к напряжениям, от расчетного напряжения — к условию прочности бруса.
^ Тема 2.1. Основные положения
.t, касательным силам — касательные напряжения sВнутренние силы, возникающие между частицами тела под действием нагрузок, являются таковыми для тела в целом. При применении метода сечений эти силы для рассматриваемой части тела являются внешними, т.е. к ним применимы методы статики. Действующая в произвольно проведенном поперечном сечении система внутренних сил эквивалентна в общем случае одной силе и одному моменту. Разложив их на составляющие, получим соответственно три силы (по направлению координатных осей) и три момента (относительно этих осей), которые называют внутренними силовыми факторами (ВСФ). Возникновение тех или иных ВСФ зависит от фактического нагружения бруса. Определяют ВСФ с помощью уравнений равновесия статики. Внутренним нормальным силам соответствуют нормальные напряжения
Вопросы для самоконтроля
1. Для чего изучается сопротивление материалов?
Сопротивление материалов — это наука, в которой рассматриваются основные понятия, принципы и методы инженерного расчета отдельных элементов конструкций и некоторых простейших конструкций на прочность, жесткость и устойчивость.
Несмотря на то, что конструктивные элементы машин и сооружений довольно разнообразны, при инженерном расчете их сводят к небольшому числу основных форм: стержни (прямые и кривые), пластины и оболочки, массивные тела. В основном, в курсе сопромата изучаются методы расчета прямых стержней при их растяжении, сжатии, кручении и изгибе.
Сопротивление материалов, как наука, основывается и на теоретических, и на экспериментальных данных.
2. Чем отличается упругая деформация от пластической?
В процессе деформации важное значение имеет величина межатомных связей, приложение нагрузки достаточной для их разыва приводит к необратимым последствиям (необратимая или пластическая деформация). Если нагрузка не превысила допустимых значений, то тело может вернуться в исходное состояние (упругая деформация). Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина. Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму.
3. Следует ли учитывать изменение размеров тел при составлении уравнений равновесия сил, приложенных к нему?
В сопротивлении материалов за расчетную модель принята модель идеализированного деформируемого тела и для решения поставленной задачи делается ряд допущений, одно из которых гласит:
· Перемещения точек элемента (или системы элементов), обусловленные его деформацией, весьма малы по сравнению с размерами самого элемента. На основе этого допущения вводится принцип начальных размеров, согласно которому при составлении уравнений равновесия элемент или систему элементов рассматривают как недеформируемое тело. Такой подход позволяет пренебречь изменениями в расположении внешних сил при деформировании реального тела.
4. В каких случаях при действии на тело нескольких сил эффект действия каждой силы можно считать независимым от действия других сил? Какое название носит этот принцип?
Системы, для которых соблюдается условие пропорциональности между напряжениями и деформациями, подчиняются принципу суперпозиции, или принципу независимости действия сил.
В соответствии с этим принципом перемещения и внутренние силы, возникающие в упругом теле, считаются независящими от порядка приложения внешних сил. То есть, если к системе приложено несколько сил, то можно определить внутренние силы, напряжения, перемещения и деформации от каждой силы в отдельности, а затем результат действия всех сил получить как сумму действий каждой силы в отдельности. Принцип независимости действия сил является одним из основных способов при решении большинства задач механики линейных систем.
5. Какими расчетными схемами заменяются реальные объекты расчета?
Расчетная схема является схематизированным представлением реальной конструкции, в котором сознательно не учитывается ряд менее важных с точки зрения проводимого расчета факторов, относящихся к конструктивным особенностям, характеру нагружения и закрепления.
Реальный объект, освобожденный от несущественных особенностей, носит название расчетной схемы.
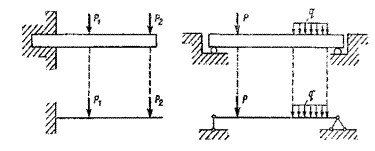
Реальные стержни изображаются их осями на расчетной схеме. Нагрузку, приложенную к небольшим участкам поверхности, заменяют силой, приложенной в точке, которую называют сосредоточенной и обозначают через Р.
Схематизируются и свойства материала. Принято рассматривать все материалы как однородную сплошную среду.
Вводятся упрощения и в геометрию конструкции. Так, все реальные тела, один размер у которых — длина, на много больше двух других (поперечных), сводятся к схеме бруса
Каковы геометрические признаки, присущие каждой расчетной схеме?
Геометрически изменяемая система — система, в которой возможны конечные перемещения без деформации элементов. При составлении расчетных схем в геометрию реального объекта вводятся определенные упрощения. Все тела представляются в виде бруса, оболочки или массивного тела.
называется элемент конструкции, длина которого существенно больше его поперечных размеров.
Рис 1.1 Балки (вверху) и их расчетные схемы (внизу)
Геометрически стержень может быть образован путем перемещения плоской фигуры вдоль некоторой кривой или прямой. Эта кривая называется осью стержня, а плоская фигура, имеющая свой центр тяжести на оси и перпендикулярная к ней, называется поперечным сечением.
По форме стержни бывают:
б) кривыми (арка, крановый крюк);
в) пространственно-изогнутыми, например пружина
6. Почему нельзя определить внутренние силовые факторы в произвольном сечении, рассматривая равновесие всего тела в целом?
7. В чем заключается метод сечений?
Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается и взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие на нее до разреза со стороны отброшенной части. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием приложенных к сечению внешних и внутренних сил (третий закон Ньютона – действие равно противодействию).
8. Можно ли с помощью метода сечений установить закон распределения внутренних силовых факторов по проведенному сечению
9. Что такое напряжение? Какова размерность напряжения?
Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле, под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения. Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.
В результате изучения темы студент должен:
иметь представлениео гипотезах, допущениях, о свойствах материалов и характере деформирования; о внутренних силовых факторах в поперечном сечении произвольно нагруженного бруса;
знатьметоды сечений; виды напряжений; основные виды деформации бруса.
Тема 2.2. Растяжение и сжатие
При изучении темы обратите внимание на гипотезу плоских сечений, которая справедлива и при других видах нагружения бруса. При растяжении или сжатии напряжения распределяются по поперечному сечению равномерно, геометрической характеристикой прочности и жесткости сечения является его площадь, форма сечения значения не имеет, все точки сечения равноопасны. Следует понять порядок расчета на прочность при растяжении и сжатии.
^ Вопросы для самоконтроля
1. В каком случае брус испытывает деформацию растяжения или сжатия?
Прямой брус испытывает деформацию центрального растяжения, сжатия, если силы или их равнодействующая действуют вдоль его оси. В этом случае в поперечном сечении бруса из шести внутренних силовых факторов отличным от нуля будет один — нормальная сила N, которая определяется методом сечений.
2. Каков закон изменения нормальных напряжений по площади поперечного сечения при растяжении и сжатии?
Чтобы понять характер напряжений и деформаций, возникающих в сжимаемом или растягиваемом брусе, представим себе прямой брус из резины, на котором нанесена сетка из продольных и поперечных линий. Если такой брус подвергнуть деформации растяжения, можно заметить, что:
· поперечные линии на брусе остаются ровными и перпендикулярными оси бруса, а расстояния между ними увеличатся;
· продольные линии останутся прямыми, а расстояния между ними уменьшатся.
Из этого эксперимента следует, что при растяжении справедлива гипотеза плоских сечений (гипотеза Бернулли), и, следовательно, все волокна бруса удлинятся на одну и ту же величину. Все это позволяет сделать вывод, что при растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению. Эти напряжения можно определить по формуле:
где N – продольная сила, А – площадь поперечного сечения бруса.
3. Влияет ли форма поперечного сечения на значение напряжений, возникающих при растяжении и сжатии?
При растяжении или сжатии напряжения распределяются по поперечному сечению равномерно, геометрической характеристикой прочности и жесткости сечения является его площадь, форма сечения значения не имеет, все точки сечения равноопасны.
4. Что называется эпюрой нормальных сил и эпюрой нормальных напряжений?
Продольной силой называется равнодействующая всех внутренних нормальных сил, возникающих в сечении. График, показывающий изменение продольных сил по длине оси бруса, называется эпюрой продольных сил (эпюрой N).
Для наглядного изображения изменения нормальных напряжений в поперечных сечениях стержня (по его длине) строится эпюра нормальных напряжений. Осью этой эпюры является отрезок прямой, равный длине стержня и параллельный его оси. При стержне постоянного сечения эпюра нормальных напряжений имеет такой же вид, как и эпюра продольных сил (она отличается от неё лишь принятым масштабом). При стержне же переменного сечения вид этих двух эпюр различен; в частности, для стержня со ступенчатым законом изменения поперечных сечений эпюра нормальных напряжений имеет скачки не только в сечениях, в которых приложены сосредоточенные осевые нагрузки (где имеет скачки эпюра продольных сил), но и в местах изменения размеров поперечных сечений.
5. Для чего строят эпюры N ? Какое поперечное сечение бруса называется опасным?sи
В результате построений мы получим график (эпюру) распределения напряжений по каждому сечению бруса, визуальное исследование которого позволяет определить наиболее напряженный участок.
Опасное сечение — это поперечное сечение, в котором действуют наибольшие внутренние усилия.
6. Что такое модуль продольной упругости материала, какова его размерность?
МОДУЛЕМ ПРОДОЛЬНОЙ УПРУГОСТИ материала называется коэффициент пропорциональности между нормальным напряжением и относительным упругим удлинением при линейном напряженном состоянии.
7. Что такое жесткость сечения бруса и жесткость бруса при растяжении (сжатии)?
Произведение модуля упругости на площадь сечения Е×А, стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.
Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение Е А / l называют жесткостью бруса при растяжении и сжатии.
8.Какова цель механических испытаний материалов?
Для определения физико — механических свойств материалов наиболее широко применяют статические испытания материалов на растяжение. Объясняется это тем, что механические характеристики, получаемые при испытании на растяжение, позволяют сравнительно точно определить поведение материала при других видах деформаций и этот вид испытаний, кроме того, наиболее легко осуществим.
9. Каковы характеристики пластичных свойств материалов?
Способность материала получать большие остаточные деформации, не разрушаясь, носит название пластичности. Мерой пластичности является удлинение d при разрыве. Чем больше d, тем более пластичным считается материал. Противоположным свойству пластичности является свойство хрупкости, т. е. способность материала разрушаться без образования заметных остаточных деформаций. Материалы, обладающие этим свойством, называются хрупкими. Для таких материалов величина удлинения при разрыве не превышает 2—5%, а в ряде случаев измеряется долями процента. Диаграмма растяжения хрупких материалов не имеет площадки текучести и зоны упрочнения.
10. Какие системы называют статически неопределимыми?
Статически неопределимыми называются такие системы, опорные реакции в которых и (или) внутренние усилия невозможно определить только из уравнений статики (уравнений равновесия).
11. Механические испытания материалов
Испытание на растяжение — это относительно простой для понимания и объяснения метод испытания материала, и, возможно, его используют чаще остальных. При проведении этого испытания, образец материала растягивают вдоль продольной оси с помощью растягивающего приспособления испытательной машины.
Испытание на сжатие
Испытания на растяжение проводить сложно, особенно, если материал хрупкий — в таких случаях наблюдается большой разброс результатов. Альтернативным методом оценки прочности материала является испытание на сжатие, которое легче провести, если материал хрупкий, так как в этом случае разброс результатов будет меньшим.
Испытание твердости — это измерение сопротивления поверхности материала воздействию инструмента, внедряемого или вдавливаемого в поверхность (индентеров), или режущего инструмента. Испытание твердости проводят для определения сопротивления материала царапанью или стиранию. Кроме того, существует приближенная зависимость между твердостью материала и пределом прочности на растяжение.
Испытание на ударную прочность — это оценка сопротивления материала мгновенному приложению нагрузки. Стандартный образец в виде балки с насечками подвергают воздействию импульсной нагрузки, создаваемой маятниковым копром.
Испытание на крип (ползучесть)
Если материал долгое время находится под нагрузкой, то под воздействием постоянного напряжения он может непрерывно деформироваться, даже несмотря на то, что величины действующих на него напряжений значительно ниже предела упругости. Эта деформация материала, зависящая от времени его нахождения под нагрузкой, называется крипом, который, в конечном итоге, ведет к разрушению материала. В частности, понимание этого явления важно, если материал используют при температурах, превышающих половину значения температуры плавления или температуры размягчения, что, например, характерно для некоторых амальгамных фаз или многих пластических материалов. При температурах на 40 — 50% меньше абсолютной точки плавления материала, крип ничтожно мал.
1.
К каким группам относятся материалы, диаграммы которых представлены на рисунках а, б и в?
- На рисунке апредставлена диаграмма растяжения образца из малоуглеродистой стали (Ст3).
- На рисунке бпредставлена диаграмма растяжения образца из чугуна.
- На рисунке впредставлена диаграмма растяжения образца из легированной стали.
- Все материалы относятся к группе хрупких.
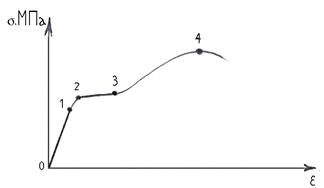
2.Указать основные характеристики прочности на диаграмме растяжения в варианте а.
Участок I соответствует упругим деформациям материала,
Участок II начинается после точки А, когда диаграмма становится криволинейной
Участок III характеризуется увеличением нагрузки, при которой происходит дальнейшая деформация образца.
Участок IV начинается в точке К и заканчивается разрушением образца в точке R. Этот участок носит название зоны разрушения.
В результате изучения темы студент должен:
иметь представлениео принципе Сен-Венана; продольных и поперечных деформациях; статически неопределимых системах при растяжении (сжатии);
знатьзакон распределения нормальных напряжений в поперечном сечении бруса; Закон Гука; порядок расчета на прочность при растяжении и сжатии; основные механические характеристики материалов;
уметьпроводить испытания материалов на растяжение.
- Тема 1.10. Работа и мощность
- Тема 1.8. Простейшие движения твердого тела
- Два условия равновесия тел в физике. Пример решения задачи на равновесие
- Действующие силы
- Первое условие равновесия системы
- Момент силы
- Второе условие равновесия системы
- Методика определения равновесия системы
- Пример решения задачи
- 🌟 Видео
Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Тема 1.10. Работа и мощность
При изучении темы обратите внимание на понятия работы, мощности, коэффициента полезного действия. Изучите единицы измерения работы и мощности и формулы их определения.
Вопросы для самоконтроля
1. Как определяется работа постоянной силы на прямолинейном пути?
W = Rs = Fs cos α,
т. е. работа силы равна произведению ее модуля на путь и на косинус угла между направлением вектора силы и направлением перемещения материальной точки.
Таким образом, работа является мерой действия силы, приложенной к материальной точке при некотором ее перемещении.
Работа является скалярной величиной.
2. Что называется мощностью?
Мощностью называется количество энергии, выделяемое или расходуемое тем или иным объектом за единицу времени
3. Что такое механический коэффициент полезного действия?
Механическим коэффициентом полезного действия (КПД) называется абсолютная величина отношения работы сил полезного сопротивления к работе движущих сил за время установившегося движения: η= Апс /Aдв.
4. Назовите формулу, позволяющую определить вращающийся момент через передаваемую мощность и угловую скорость вращения тела при равномерном вращении.
Если работа совершается силой, приложенной к равномерно вращающемуся телу, то мощность в этом случае может быть определена по формуле:
P = W/t = Tφ/t или P = Tω.
Следовательно, вращающий момент можно определить по формуле: T= P/ω
В результате изучения темы студент должен:
иметь представлениео работе переменной силы; зависимости вращающегося момента от угловой скорости и передаваемой мощности;
знатьформулы определения работы мощности при поступательном и вращательном движениях тел.
Раздел 2. ОСНОВЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Изучение курса сопротивления материалов (наука о прочности, жесткости и устойчивости деформируемых под нагрузкой элементов машин и конструкций) следует начать с повторения раздела «Статика» (равновесие тел, уравнения равновесия, геометрические характеристики сечений). Непременными условиями успешного овладения учебным материалом являются: а) четкое понимание физического смысла рассматриваемых понятий; б) свободное владение методом сечений; в) осознанное применение геометрических характеристик прочности и жесткости поперечных сечений; г) самостоятельное решение достаточно большого числа задач. Принципиальная схема изучения каждого из видов нагружения бруса (старый термин «вид деформации») единообразна: от внешних сил с помощью метода сечения к внутренним силовым факторам, от них — к напряжениям, от расчетного напряжения — к условию прочности бруса.
^ Тема 2.1. Основные положения
.t, касательным силам — касательные напряжения sВнутренние силы, возникающие между частицами тела под действием нагрузок, являются таковыми для тела в целом. При применении метода сечений эти силы для рассматриваемой части тела являются внешними, т.е. к ним применимы методы статики. Действующая в произвольно проведенном поперечном сечении система внутренних сил эквивалентна в общем случае одной силе и одному моменту. Разложив их на составляющие, получим соответственно три силы (по направлению координатных осей) и три момента (относительно этих осей), которые называют внутренними силовыми факторами (ВСФ). Возникновение тех или иных ВСФ зависит от фактического нагружения бруса. Определяют ВСФ с помощью уравнений равновесия статики. Внутренним нормальным силам соответствуют нормальные напряжения
Вопросы для самоконтроля
1. Для чего изучается сопротивление материалов?
Сопротивление материалов — это наука, в которой рассматриваются основные понятия, принципы и методы инженерного расчета отдельных элементов конструкций и некоторых простейших конструкций на прочность, жесткость и устойчивость.
Несмотря на то, что конструктивные элементы машин и сооружений довольно разнообразны, при инженерном расчете их сводят к небольшому числу основных форм: стержни (прямые и кривые), пластины и оболочки, массивные тела. В основном, в курсе сопромата изучаются методы расчета прямых стержней при их растяжении, сжатии, кручении и изгибе.
Сопротивление материалов, как наука, основывается и на теоретических, и на экспериментальных данных.
2. Чем отличается упругая деформация от пластической?
В процессе деформации важное значение имеет величина межатомных связей, приложение нагрузки достаточной для их разыва приводит к необратимым последствиям (необратимая или пластическая деформация). Если нагрузка не превысила допустимых значений, то тело может вернуться в исходное состояние (упругая деформация). Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина. Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму.
3. Следует ли учитывать изменение размеров тел при составлении уравнений равновесия сил, приложенных к нему?
В сопротивлении материалов за расчетную модель принята модель идеализированного деформируемого тела и для решения поставленной задачи делается ряд допущений, одно из которых гласит:
· Перемещения точек элемента (или системы элементов), обусловленные его деформацией, весьма малы по сравнению с размерами самого элемента. На основе этого допущения вводится принцип начальных размеров, согласно которому при составлении уравнений равновесия элемент или систему элементов рассматривают как недеформируемое тело. Такой подход позволяет пренебречь изменениями в расположении внешних сил при деформировании реального тела.
4. В каких случаях при действии на тело нескольких сил эффект действия каждой силы можно считать независимым от действия других сил? Какое название носит этот принцип?
Системы, для которых соблюдается условие пропорциональности между напряжениями и деформациями, подчиняются принципу суперпозиции, или принципу независимости действия сил.
В соответствии с этим принципом перемещения и внутренние силы, возникающие в упругом теле, считаются независящими от порядка приложения внешних сил. То есть, если к системе приложено несколько сил, то можно определить внутренние силы, напряжения, перемещения и деформации от каждой силы в отдельности, а затем результат действия всех сил получить как сумму действий каждой силы в отдельности. Принцип независимости действия сил является одним из основных способов при решении большинства задач механики линейных систем.
5. Какими расчетными схемами заменяются реальные объекты расчета?
Расчетная схема является схематизированным представлением реальной конструкции, в котором сознательно не учитывается ряд менее важных с точки зрения проводимого расчета факторов, относящихся к конструктивным особенностям, характеру нагружения и закрепления.
Реальный объект, освобожденный от несущественных особенностей, носит название расчетной схемы.
Реальные стержни изображаются их осями на расчетной схеме. Нагрузку, приложенную к небольшим участкам поверхности, заменяют силой, приложенной в точке, которую называют сосредоточенной и обозначают через Р.
Схематизируются и свойства материала. Принято рассматривать все материалы как однородную сплошную среду.
Вводятся упрощения и в геометрию конструкции. Так, все реальные тела, один размер у которых — длина, на много больше двух других (поперечных), сводятся к схеме бруса
Каковы геометрические признаки, присущие каждой расчетной схеме?
Геометрически изменяемая система — система, в которой возможны конечные перемещения без деформации элементов. При составлении расчетных схем в геометрию реального объекта вводятся определенные упрощения. Все тела представляются в виде бруса, оболочки или массивного тела.
называется элемент конструкции, длина которого существенно больше его поперечных размеров.
Рис 1.1 Балки (вверху) и их расчетные схемы (внизу)
Геометрически стержень может быть образован путем перемещения плоской фигуры вдоль некоторой кривой или прямой. Эта кривая называется осью стержня, а плоская фигура, имеющая свой центр тяжести на оси и перпендикулярная к ней, называется поперечным сечением.
По форме стержни бывают:
б) кривыми (арка, крановый крюк);
в) пространственно-изогнутыми, например пружина
6. Почему нельзя определить внутренние силовые факторы в произвольном сечении, рассматривая равновесие всего тела в целом?
7. В чем заключается метод сечений?
Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается и взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие на нее до разреза со стороны отброшенной части. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием приложенных к сечению внешних и внутренних сил (третий закон Ньютона – действие равно противодействию).
8. Можно ли с помощью метода сечений установить закон распределения внутренних силовых факторов по проведенному сечению
9. Что такое напряжение? Какова размерность напряжения?
Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле, под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения. Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.
В результате изучения темы студент должен:
иметь представлениео гипотезах, допущениях, о свойствах материалов и характере деформирования; о внутренних силовых факторах в поперечном сечении произвольно нагруженного бруса;
знатьметоды сечений; виды напряжений; основные виды деформации бруса.
Тема 2.2. Растяжение и сжатие
При изучении темы обратите внимание на гипотезу плоских сечений, которая справедлива и при других видах нагружения бруса. При растяжении или сжатии напряжения распределяются по поперечному сечению равномерно, геометрической характеристикой прочности и жесткости сечения является его площадь, форма сечения значения не имеет, все точки сечения равноопасны. Следует понять порядок расчета на прочность при растяжении и сжатии.
^ Вопросы для самоконтроля
1. В каком случае брус испытывает деформацию растяжения или сжатия?
Прямой брус испытывает деформацию центрального растяжения, сжатия, если силы или их равнодействующая действуют вдоль его оси. В этом случае в поперечном сечении бруса из шести внутренних силовых факторов отличным от нуля будет один — нормальная сила N, которая определяется методом сечений.
2. Каков закон изменения нормальных напряжений по площади поперечного сечения при растяжении и сжатии?
Чтобы понять характер напряжений и деформаций, возникающих в сжимаемом или растягиваемом брусе, представим себе прямой брус из резины, на котором нанесена сетка из продольных и поперечных линий. Если такой брус подвергнуть деформации растяжения, можно заметить, что:
· поперечные линии на брусе остаются ровными и перпендикулярными оси бруса, а расстояния между ними увеличатся;
· продольные линии останутся прямыми, а расстояния между ними уменьшатся.
Из этого эксперимента следует, что при растяжении справедлива гипотеза плоских сечений (гипотеза Бернулли), и, следовательно, все волокна бруса удлинятся на одну и ту же величину. Все это позволяет сделать вывод, что при растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению. Эти напряжения можно определить по формуле:
где N – продольная сила, А – площадь поперечного сечения бруса.
3. Влияет ли форма поперечного сечения на значение напряжений, возникающих при растяжении и сжатии?
При растяжении или сжатии напряжения распределяются по поперечному сечению равномерно, геометрической характеристикой прочности и жесткости сечения является его площадь, форма сечения значения не имеет, все точки сечения равноопасны.
4. Что называется эпюрой нормальных сил и эпюрой нормальных напряжений?
Продольной силой называется равнодействующая всех внутренних нормальных сил, возникающих в сечении. График, показывающий изменение продольных сил по длине оси бруса, называется эпюрой продольных сил (эпюрой N).
Для наглядного изображения изменения нормальных напряжений в поперечных сечениях стержня (по его длине) строится эпюра нормальных напряжений. Осью этой эпюры является отрезок прямой, равный длине стержня и параллельный его оси. При стержне постоянного сечения эпюра нормальных напряжений имеет такой же вид, как и эпюра продольных сил (она отличается от неё лишь принятым масштабом). При стержне же переменного сечения вид этих двух эпюр различен; в частности, для стержня со ступенчатым законом изменения поперечных сечений эпюра нормальных напряжений имеет скачки не только в сечениях, в которых приложены сосредоточенные осевые нагрузки (где имеет скачки эпюра продольных сил), но и в местах изменения размеров поперечных сечений.
5. Для чего строят эпюры N ? Какое поперечное сечение бруса называется опасным?sи
В результате построений мы получим график (эпюру) распределения напряжений по каждому сечению бруса, визуальное исследование которого позволяет определить наиболее напряженный участок.
Опасное сечение — это поперечное сечение, в котором действуют наибольшие внутренние усилия.
6. Что такое модуль продольной упругости материала, какова его размерность?
МОДУЛЕМ ПРОДОЛЬНОЙ УПРУГОСТИ материала называется коэффициент пропорциональности между нормальным напряжением и относительным упругим удлинением при линейном напряженном состоянии.
7. Что такое жесткость сечения бруса и жесткость бруса при растяжении (сжатии)?
Произведение модуля упругости на площадь сечения Е×А, стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.
Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение Е А / l называют жесткостью бруса при растяжении и сжатии.
8.Какова цель механических испытаний материалов?
Для определения физико — механических свойств материалов наиболее широко применяют статические испытания материалов на растяжение. Объясняется это тем, что механические характеристики, получаемые при испытании на растяжение, позволяют сравнительно точно определить поведение материала при других видах деформаций и этот вид испытаний, кроме того, наиболее легко осуществим.
9. Каковы характеристики пластичных свойств материалов?
Способность материала получать большие остаточные деформации, не разрушаясь, носит название пластичности. Мерой пластичности является удлинение d при разрыве. Чем больше d, тем более пластичным считается материал. Противоположным свойству пластичности является свойство хрупкости, т. е. способность материала разрушаться без образования заметных остаточных деформаций. Материалы, обладающие этим свойством, называются хрупкими. Для таких материалов величина удлинения при разрыве не превышает 2—5%, а в ряде случаев измеряется долями процента. Диаграмма растяжения хрупких материалов не имеет площадки текучести и зоны упрочнения.
10. Какие системы называют статически неопределимыми?
Статически неопределимыми называются такие системы, опорные реакции в которых и (или) внутренние усилия невозможно определить только из уравнений статики (уравнений равновесия).
11. Механические испытания материалов
Испытание на растяжение — это относительно простой для понимания и объяснения метод испытания материала, и, возможно, его используют чаще остальных. При проведении этого испытания, образец материала растягивают вдоль продольной оси с помощью растягивающего приспособления испытательной машины.
Испытание на сжатие
Испытания на растяжение проводить сложно, особенно, если материал хрупкий — в таких случаях наблюдается большой разброс результатов. Альтернативным методом оценки прочности материала является испытание на сжатие, которое легче провести, если материал хрупкий, так как в этом случае разброс результатов будет меньшим.
Испытание твердости — это измерение сопротивления поверхности материала воздействию инструмента, внедряемого или вдавливаемого в поверхность (индентеров), или режущего инструмента. Испытание твердости проводят для определения сопротивления материала царапанью или стиранию. Кроме того, существует приближенная зависимость между твердостью материала и пределом прочности на растяжение.
Испытание на ударную прочность — это оценка сопротивления материала мгновенному приложению нагрузки. Стандартный образец в виде балки с насечками подвергают воздействию импульсной нагрузки, создаваемой маятниковым копром.
Испытание на крип (ползучесть)
Если материал долгое время находится под нагрузкой, то под воздействием постоянного напряжения он может непрерывно деформироваться, даже несмотря на то, что величины действующих на него напряжений значительно ниже предела упругости. Эта деформация материала, зависящая от времени его нахождения под нагрузкой, называется крипом, который, в конечном итоге, ведет к разрушению материала. В частности, понимание этого явления важно, если материал используют при температурах, превышающих половину значения температуры плавления или температуры размягчения, что, например, характерно для некоторых амальгамных фаз или многих пластических материалов. При температурах на 40 — 50% меньше абсолютной точки плавления материала, крип ничтожно мал.
1.
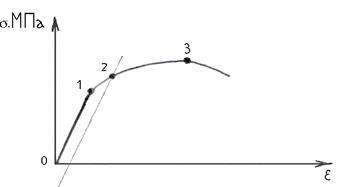
К каким группам относятся материалы, диаграммы которых представлены на рисунках а, б и в?
- На рисунке апредставлена диаграмма растяжения образца из малоуглеродистой стали (Ст3).
- На рисунке бпредставлена диаграмма растяжения образца из чугуна.
- На рисунке впредставлена диаграмма растяжения образца из легированной стали.
- Все материалы относятся к группе хрупких.
2.Указать основные характеристики прочности на диаграмме растяжения в варианте а.
Участок I соответствует упругим деформациям материала,
Участок II начинается после точки А, когда диаграмма становится криволинейной
Участок III характеризуется увеличением нагрузки, при которой происходит дальнейшая деформация образца.
Участок IV начинается в точке К и заканчивается разрушением образца в точке R. Этот участок носит название зоны разрушения.
В результате изучения темы студент должен:
иметь представлениео принципе Сен-Венана; продольных и поперечных деформациях; статически неопределимых системах при растяжении (сжатии);
знатьзакон распределения нормальных напряжений в поперечном сечении бруса; Закон Гука; порядок расчета на прочность при растяжении и сжатии; основные механические характеристики материалов;
уметьпроводить испытания материалов на растяжение.
Видео:2.4. Равновесие произвольной плоской системы сил (1 из 4)Скачать

Тема 1.8. Простейшие движения твердого тела
В результате изучения темы студент должен:
иметь представлениео видах движения тела и их признаках;
знать параметры, характеризующие движение тела вокруг неподвижной оси движения отдельных его точек для любого вида движения.
Вопросы для самоконтроля
1. Какое движение твердого тела называется поступательным?
2. Перечислите свойства поступательного движения твердого тела.
3. Дайте определение вращательного движения твердого тела вокруг неподвижной оси.
4. Как записывается в общем виде уравнение вращательного движения твердого тела?
5. Напишите формулу, устанавливающую связь между частотой вращения тела п и угловой скоростью вращения.
6. Дайте определение равномерного и равнопеременного вращательного движения.
7. Какая дифференциальная зависимость существует между угловым перемещением, угловой скоростью и угловым ускорением?
8. Какая зависимость существует между линейным перемещением, скоростью и ускорением точек вращающегося тела и угловым перемещением, скоростью и ускорением тела.
ДИНАМИКА
При изучении раздела вникните в физический смысл аксиом динамики, научитесь использовать основанный на принципе Даламбера метод кинетостатики, позволяющий применять уравнения равновесия статики для движущегося с ускорением тела. Следует помнить, что сила инерции прилагается к ускоренному телу условно, так как в действительности на него не действует. Особое внимание следует уделить вопросу трения скольжения и понятию самоторможения, имеющим важнейшее значение в технике. Формулы для определения работы, мощности и кинетической энергии тела, а также основной закон динамики для случаев поступательного и вращательного движения тела имеют полную смысловую аналогию (таблица).
| Понятие | Основные параметры | Поступательные движения | Вращательное движение |
| Кинематика | Расстояние Скорость Ускорение | S = ¦(t) V = S’ at = V’ | j = ¦(t) w = j’ e = w’ |
| Динамика | Силовое воздействие Сила инертности тела Основной закон динамики Работа Мощность Кинематическая энергия | Сила F Масса m F = ma W = FS P = FV m · V 2 Ek = __________ 2 | Момент M Динамический момент инерции J M = Je W = Mj P = Mw J · w 2 Ek = __________ 2 |
Тема 1.9. Основные понятия и аксиомы динамики
В результате изучения темы студент должен:
иметь представлениео двух основных задачах динамики;
знать аксиомы динамики при рассмотрении механического состояния тела.
Вопросы для самоконтроля
1. Сформулируйте первую аксиому динамики (принцип инерции) и вторую аксиому динамики (основной закон динамики точки).
2. Сформулируйте две основные задачи динамики.
3. Изложите третью аксиому динамики (закон независимости действия сил) и четвертую аксиому (закон равенства действия и противодействия).
Тема 1.10. Работа и мощность
В результате изучения темы студент должен:
иметь представлениео работе переменной силы; зависимости вращающегося момента от угловой скорости и передаваемой мощности;
знатьформулы определения работы мощности при поступательном и вращательном движениях тел.
Вопросы для самоконтроля
1. Как определяется работа постоянной силы на прямолинейном пути?
2. Что называется мощностью?
3. Что такое механический коэффициент полезного действия?
4. Назовите формулу, позволяющую определить вращающийся момент через передаваемую мощность и угловую скорость вращения тела при равномерном вращении.
Раздел 2. СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Изучение курса сопротивления материалов (наука о прочности, жесткости и устойчивости деформируемых под нагрузкой элементов машин и конструкций) следует начать с повторения раздела «Статика» (равновесие тел, уравнения равновесия, геометрические характеристики сечений). Непременными условиями успешного овладения учебным материалом являются: а) четкое понимание физического смысла рассматриваемых понятий; б) свободное владение методом сечений; в) осознанное применение геометрических характеристик прочности и жесткости поперечных сечений; г) самостоятельное решение достаточно большого числа задач. Принципиальная схема изучения каждого из видов нагружения бруса (старый термин «вид деформации») единообразна: от внешних сил с помощью метода сечения к внутренним силовым факторам, от них — к напряжениям, от расчетного напряжения — к условию прочности бруса.
Тема 2.1. Основные положения
В результате изучения темы студент должен:
иметь представлениео гипотезах, допущениях, о свойствах материалов и характере деформирования; о внутренних силовых факторах в поперечном сечении произвольно нагруженного бруса;
знатьметоды сечений; виды напряжений; основные виды деформации бруса.
Вопросы для самоконтроля
1. Для чего изучается сопротивление материалов?
2. Чем отличается упругая деформация от пластической?
3. Следует ли учитывать изменение размеров тел при составлении уравнений равновесия сил, приложенных к нему?
4. В каких случаях при действии на тело нескольких сил эффект действия каждой силы можно считать независимым от действия других сил? Какое название носит этот принцип?
5. Какими расчетными схемами заменяются реальные объекты расчета? Каковы геометрические признаки, присущие каждой расчетной схеме?
6. Почему нельзя определить внутренние силовые факторы в произвольном сечении, рассматривая равновесие всего тела в целом?
7. В чем заключается метод сечений?
8. Можно ли с помощью метода сечений установить закон распределения внутренних силовых факторов по проведенному сечению?
9. Что такое напряжение? Какова размерность напряжения?
Тема 2.2. Растяжение и сжатие
В результате изучения темы студент должен:
иметь представлениео принципе Сен-Венана; продольных и поперечных деформациях; статически неопределимых системах при растяжении (сжатии);
знатьзакон распределения нормальных напряжений в поперечном сечении бруса; Закон Гука; порядок расчета на прочность при растяжении и сжатии; основные механические характеристики материалов;
уметьпроводить испытания материалов на растяжение.
Вопросы для самоконтроля
1. В каком случае брус испытывает деформацию растяжения или сжатия?
2. Каков закон изменения нормальных напряжений по площади поперечного сечения при растяжении и сжатии?
3. Влияет ли форма поперечного сечения на значение напряжений, возникающих при растяжении и сжатии?
4. Что называется эпюрой нормальных сил и эпюрой нормальных напряжений?
5. Для чего строят эпюры N и s? Какое поперечное сечение бруса называется опасным?
6. Что такое модуль продольной упругости материала, какова его размерность?
7. Что такое жесткость сечения бруса и жесткость бруса при растяжении (сжатии)?
8. Какова цель механических испытаний материалов?
9. Каковы характеристики пластичных свойств материалов?
10. Какие системы называют статически неопределимыми?
Видео:Определение реакций опор простой рамыСкачать

Два условия равновесия тел в физике. Пример решения задачи на равновесие
Раздел физики, который изучает покоящиеся тела с точки зрения механики, называется статикой. Ключевыми моментами статики являются понимание условий равновесия тел в системе и умение применять эти условия для решения практических задач.
Видео:Видеоурок 2. Определение реакций двухопорных балок.Скачать

Действующие силы
Причиной вращения, поступательного перемещения или сложного движения тел по кривым траекториям является действие внешней ненулевой силы на эти тела. В физике силой называется величина, которая, воздействуя на тело, способна придать ему ускорение, то есть изменить количество движения. Изучают эту величину с давних времен, тем не менее, законы статики и динамики окончательно оформились в стройную физическую теорию только с приходом нового времени. Большую роль в становлении механики движения сыграли работы Исаака Ньютона, в честь которого сейчас называют единицу измерения силы ньютоном.
При рассмотрении условий равновесия тел в физике важно знать несколько параметров действующих сил. К ним относятся следующие:
- направление действия;
- абсолютное значение;
- точка приложения;
- угол между рассматриваемой силой и другими приложенными к системе силами.
Совокупность перечисленных параметров позволяет однозначно сказать, будет данная система двигаться или покоиться.
Видео:2.4. Равновесие произвольной плоской системы сил (3 из 4)Скачать

Первое условие равновесия системы
Когда система твердых тел не будет поступательно перемещаться в пространстве? Ответ на этот вопрос станет понятен, если вспомнить второй ньютоновский закон. Согласно ему, система не будет совершать поступательного перемещения тогда и только тогда, когда сумма внешних по отношению к системе сил равна нулю. То есть первое условие равновесия твердых тел математически выглядит так:
Здесь n — число внешних сил в системе. Приведенное выражение предполагает векторное суммирование сил.
Рассмотрим простой случай. Предположим, что на тело действуют две силы одинаковые по величине, но направленные в разные стороны. В итоге одна из них будет стремиться придать ускорение телу вдоль положительного направления произвольно выбранной оси, а другая — вдоль отрицательного. Результатом их действия будет покоящееся тело. Векторная сумма этих двух сил будет равна нулю. Справедливости ради отметим, что описанный пример приведет к появлению растягивающих напряжений в теле, но к теме статьи этот факт не относится.
Для облегчения проверки записанного условия равновесия тел можно воспользоваться геометрическим изображением всех сил в системе. Если их векторы расположить так, чтобы каждая последующая сила начиналась из конца предыдущей, тогда записанное равенство будет выполняться, когда начало первой силы совпадет с концом последней. Геометрически это выглядит в виде замкнутого контура из векторов сил.
Видео:Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решениеСкачать

Момент силы
Прежде чем переходить к описанию следующего условия равновесия твердого тела, необходимо ввести важное физическое понятие статики — момент силы. Говоря простым языком, скалярная величина момента силы — это произведение модуля самой силы на радиус-вектор от оси вращения до точки приложения силы. Иными словами, момент силы имеет смысл рассматривать только относительно какой-либо оси вращения системы. Скалярная математическая форма записи момента силы выглядит так:
Где d — плечо силы.
Из записанного выражения следует, что если сила F приложена к любой точке оси вращения под любым углом к ней, то ее момент силы будет равен нулю.
Физический смысл величины M заключается в способности силы F совершать поворот. Эта способность возрастает с увеличением расстояния между точкой приложения силы и осью вращения.
Видео:Математика это не ИсламСкачать

Второе условие равновесия системы
Как можно догадаться, второе условие равновесия тел с моментом силы связано. Сначала приведем соответствующую математическую формулу, а затем разберем ее подробнее. Итак, условие отсутствия вращения в системе записывается так:
То есть сумма моментов всех сил должна быть равна нулю относительно каждой оси вращения в системе.
Момент силы является векторной величиной, однако для определения вращательного равновесия важно знать лишь знак данного момента Mi. Следует запомнить, что если сила стремится совершить вращение по ходу стрелки часов, значит, она создает отрицательный момент. Наоборот, вращение против хода стрелки приводит к появлению положительного момента Mi.
Видео:Введение в СопроматСкачать

Методика определения равновесия системы
Выше были приведены два условия равновесия тел. Очевидно, что для того чтобы тело не двигалось и находилось в покое, необходимо одновременное выполнение обоих условий.
При решении задач на равновесие следует рассматривать систему из записанных двух уравнений. Решение этой системы даст ответ на любую задачу по статике.
Иногда первое условие, отражающее отсутствие поступательного движения, может не давать никакой полезной информации, тогда решение задачи сводится к анализу условия моментов.
При рассмотрении проблем статики на условия равновесия тел центр тяжести тела играет важную роль, поскольку именно через него проходит ось вращения. Если сумма моментов сил относительно центра тяжести будет равна нулю, тогда вращение системы наблюдаться не будет.
Видео:Физика. 7 класс. Определение размера малых тел методом рядов /25.09.2020/Скачать

Пример решения задачи
Известно, что на концы невесомой доски положили два груза. Масса правого груза в два раза больше, чем масса левого. Необходимо определить положение опоры под доской, при которой данная система находилась бы в равновесии.
Обозначим длину доски буквой l, а расстояние от ее левого конца до опоры — буквой x. Ясно, что данная система не испытывает никакого поступательного движения, поэтому первое условие для решения задачи применять не нужно.
Вес каждого груза создает момент силы относительно опоры, причем оба момента имеют разный знак. В выбранных нами обозначениях, второе условие равновесия будет иметь вид:
Здесь P1 и P2 — веса левого и правого грузов, соответственно. Разделив на P1 обе части равенства, и используя условие задачи, получаем:
Таким образом, чтобы система находилась в равновесии, опора должна располагаться на 2/3 длины доски от левого ее конца (на 1/3 от правого конца).
🌟 Видео
Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Урок 94. Вычисление моментов инерции телСкачать

Видеоурок 1. Определение реакций жёстких стержней.Скачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать

Сопротивление материалов. Лекция 1 (введение).Скачать

Сперматозоид-чемпион | наглядно показано оплодотворениеСкачать

📚Лекция VI-1. Теория предельного равновесияСкачать

Лекция IV-3. Напряженное состояние под внешней нагрузкой. Часть 1Скачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

РГР Д6 Принцип ДаламбераСкачать

Сопротивление материалов. A-01 (введение).Скачать