Приток нефти, газа, воды и их смесей к забоям скважин происходит при образовании на забое скважин давления меньше-
го, чем в продуктивном пласте. При разработке нефтяных залежей приток нефти (жидкости) и газа к скважинам происходит по радиально сходящимся к скважинам линиям.
По мере приближения жидкости и газа к скважине площади этих поверхностей непрерывно уменьшаются, а скорости фильтрации жидкости при постоянном расходе непрерывно увеличиваются, достигая максимума у стенок скважины. Таким образом, на перемещение единицы объема жидкости в направлении скважины должны непрерывно возрастать затраты энергии и связанные с этим перепады давления на единицу длины пути.
Скорость фильтрации жидкости в пористой среде, согласно закону А. Дарси (французский инженер), прямо пропорциональна перепаду давления и обратно пропорциональна вязкости жидкости:
(27)
где v — скорость линейной фильтрации; Q — объемный расход жидкости через породу за 1 с; F — площадь фильтрации; k — коэффициент проницаемости породы; ^ — вязкость жидкости; АР -перепад давления; А/ — длина элемента фильтрации жидкости. Коэффициент проницаемости из уравнения (27) будет
На расстоянии г от центра скважины площадь фильтрации F = 2лг • h, а длина элемента А/ = Аг; подставляя эти значения в формулу (27), получим
(28)
(29)
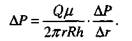
где Q — дебит скважины, м 3 ; /и — вязкость жидкости, Па-с; RK —радиус контура питания, м; R — коэффициент проницаемости пласта, м 2 ; h — толщина продуктивного пласта, м; гс — радиус скважины, м.
Задавая различные значения /?к и решая уравнение (29) относительно Рпл (при условии Рзаб = const), получим изменение давления в любом направлении вокруг скважины при установившемся притоке в виде логарифмической кривой (рис. 25), называемой воронкой депрессии.
Рис. 25. Кривые распределения давления в пласте вокруг добывающей скважины
Как видно из рис. 25, основной перепад давления в пласте происходит в непосредственной близости от скважины. По мере удаления от нее кривая распределения давления выполаживается, что говорит о значительном уменьшении скоростей фильтрации и удалением от скважины. Записав уравнение относительно Q,
получим уравнение Ж. Дюпюи для радиально установившегося притока однородной жидкости в скважину:
(30)
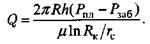
Данное уравнение применимо для так называемой гидродинамически совершенной скважины.
За гидродинамически совершенную скважину в нефтепромысловой практике принимают скважину с открытым забоем, где фильтрационные потоки движутся к скважине параллельно друг другу, кровле и подошве пласта (рис. 26 а).
Рис. 26. Виды гидродинамического несовершенства скважин
Скважины чаще всего гидродинамически несовершенны. Гидродинамическое несовершенство скважин проявляется появлением дополнительных сопротивлений, возникающих в при-забойной зоне у стенок скважины вследствие отклонения потока жидкости от плоскопараллельного, а также в результате сгущения линий токов у перфорационных отверстий, вызывающих местное повышение скоростей движения жидкости.
Бывают гидродинамически несовершенные скважины по степени вскрытия, где продуктивные пласты вскрывают не на всю толщину (рис. 26 б). Линии тока к этим скважинам от кровли
до забоя параллельны, а ниже уровня забоя искривляются, в результате чего возникают дополнительные гидравлические сопротивления. По характеру вскрытия большая часть скважин является гидродинамически несовершенной. При этом вскрывается продуктивный пласт на всю его толщину, но сообщение с ним происходит через перфорационные отверстия в эксплуатационной колонне (рис. 26 в).
Встречаются также скважины несовершенные и по степени, и по характеру вскрытия (рис. 26 г).
Уравнение движения жидкости в несовершенную скважину описывается следующей формулой:
(31)
где QH — дебит жидкости гидродинамически несовершенной скважины и по характеру, и по степени вскрытия.
Отношение дебита жидкости гидродинамически несовершенной скважины к дебиту жидкости гидродинамически совершенной при равных условиях называется коэффициентом гидродинамического несовершенства скважины, который всегда меньше единицы, то есть выражается в долях от 1:
(32)
где Q — дебит гидродинамически совершенной скважины.
Но коэффициент с трудно определить, так как неизвестно, сколько отверстий образовалось в результате перфорации, какова глубина и диаметр этих отверстий. Поэтому вместо гидродинамически несовершенной скважины принимается гидродинамически совершенная скважина с меньшим радиусом. Радиус этой условной скважины называется приведенным, а дебит ее
(33)
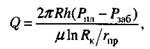
где г — приведенный радиус скважины, который определяется
расчетным путем по данным гидродинамических исследований скважин.
Как уже отмечалось, на жидкость, газ и воду в пласте действует пластовое давление.
Пластовое давление — это давление, замеренное в остановленной (закрытой) скважине. Уровень жидкости в скважине, установившийся при этом, называется статическим уровнем. Расстояние до уровня в скважине измеряется от устья, а высота столба жидкости — от забоя до статического уровня:
(34)
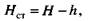
где Яст — статический уровень в скважине, м; Я — глубина скважины, м; h — расстояние от устья до уровня в скважине, м.
В случае когда пластовое давление превышает давление столба жидкости в заполненной скважине, при открытом устье жидкость будет переливаться из скважины.
В работающей скважине давление на забое (забойное давление) устанавливается ниже пластового, и в затрубном пространстве скважины устанавливается другой уровень жидкости, который называется динамическим уровнем. Динамический уровень всегда меньше статического.
Объем нефти, поступающей к забою скважины, зависит от коллекторских свойств пласта, вязкости нефти и перепада давления, то есть разницы между пластовым и забойным давлением. Наибольшая зависимость наблюдается между дебитом (количеством) поступающей жидкости к забою скважины и перепадом давления.
Уравнение притока нефти (жидкости) к скважине при этом записывается как
(35)
где Q — дебит нефти (жидкости), т/сут; К — коэффициент продуктивности, равный приросту дебита скважины в сутки на единицу снижения забойного давления при постоянном пластовом давлении (Рпл = const); Рпл — пластовое давление, МПа; Р3 — забойное давление, МПа.
Когда известны коэффициент продуктивности и пластовое давление, определяется дебит скважины при определенном снижении забойного давления.
На практике коэффициент продуктивности определяют по данным исследовательских работ в скважине. На определен-
ном режиме работы скважины замеряют дебит нефти (жидкости) и одновременно замеряется забойное давление. После этого меняют режим работы скважины и вновь замеряют дебит и забойное давление. По результатам определяется зависимость дебита скважины от забойного давления. Зная дебиты жидкости и соответствующие им перепады давления (депрессии), строят кривую зависимости притока жидкости от перепада давлений, которая называется индикаторной линией. Строят график, на котором по вертикальной оси откладывают значения перепадов давлений, а по горизонтальной оси откладывают значения деби-тов жидкости. На графике каждому значению перепада давления соответствует определенный дебит жидкости.
Индикаторные линии могут быть прямыми и выпуклыми и вогнутыми относительно оси дебитов (кривые рис. 27). Выпуклые индикаторные кривые бывают, когда вместе с нефтью извлекается газ или при больших перепадах давления.
Теоретически, при соблюдении закона Дарси, максимальная производительность скважины может быть при Ртб = 0, и эту производительность называют потенциальным дебитом:
Рис. 27. Индикаторные линии (зависимости дебита жидкости от перепада давления)
Но практически потенциального дебита получить невозможно, так как в скважине сохраняется какой-то столб жидкости. 11ри исследовании скважин дебиты нефти замеряют на поверхности в ГЗУ (групповые замерные установки) за соответствующую единицу времени, пересчитываемую на дебит жидкости скважины в м 3 или тоннах в сутки. Дебиты газа замеряются газовыми счетчиками-расходомерами. Пластовые давления замеряются С Помощью глубинных манометров, спускаемых в скважины на утильной проволоке.
Видео:Траектория и уравнения движения точки. Задача 1Скачать
Приток газа к скважине по закону Дарси
Исследуем установившийся плоскорадиальный фильтрационный поток идеального газа. Для этого воспользуемся аналогией между фильтрацией несжимаемой жидкости и газа. Запишем формулу дебита совершенной скважины для несжимаемой жидкости:
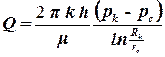 . | (3.17) |
Произведем в этом уравнении замены. Заменим давление p на функцию Лейбензона P, а объемный расход Q на массовый расход Qm.
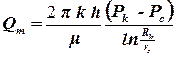 . | (3.18) |
В последней формуле распишем функцию Лейбензона, тогда массовый дебит газовой скважины будет рассчитываться по формуле:
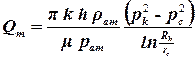 , | (3.19) |
а приведенный к атмосферным условиям объемный расход
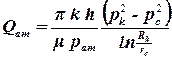 . | (3.20) |
Расчет распределения давления вокруг газовой скважины производится в той же последовательности:
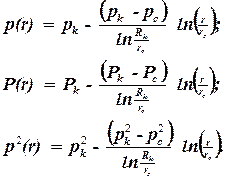 | (3.21) |
Скорости фильтрации в любой точки вокруг скважины можно найти из уравнения неразрывности:
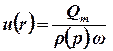 . | (3.22) |
На Рис. 3.2.a, и b приведены распределение давления и скорости фильтрации вокруг газовой скважины. У газовой скважины падение давления вблизи скважины больше, чем у нефтяной, поэтому при прочих равных условиях и скорости фильтрации у газовой скважины уменьшается быстрее, чем у нефтяной скважины.
Рис. 3.2  . Распределение давления a) и отношение скорости фильтрации в пласте к скорости фильтрации на скважине б) для газовой скважины |
Дата добавления: 2015-09-25 ; просмотров: 1596 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать
Режимы разработки нефтегазоносных пластов
Постановка и решение газогидродинамических задач разработки месторождений в значительной степени определяются природой движущих сил, обеспечивающих фильтрацию нефти или газа в пласте. Поэтому важно знать режим разработки нефтегазоносных пластов.
На рисунке 1.6 представлена схема нефтегазового месторождения. Верхнюю часть его занимает газ (газовая шапка). В газовых месторождениях газ занимает большую часть месторождения, в нефтяных – меньшую или его совсем нет. Ниже находится нефть. В газовых месторождениях эту область называют нефтяной оторочкой. Ещё ниже находится вода. Если она подпирает нефть по всей ширине месторождения снизу, то она называется подошвенной, а если по краям месторождения, как на рисунке, то краевой.
 Рисунок 1.6 – Схема нефтегазового месторождения |
Режимом нефтегазового пласта называется проявление доминирующей формы пластовой энергии в процессе разработки залежи нефти или газа. Потенциальная энергия пласта выражается в следующих формах:
· потенциальной энергии давления воды на нефтяной пласт;
· потенциальной энергии давления газа в газовой шапке;
· потенциальной энергии растворённого в нефти газа;
· потенциальной энергии упругой деформации жидкости и породы пласта;
Рисунок 1.7 – Схема к водонапорному режиму · потенциальной энергии, обусловленной силой тяжести пластовых жидкостей. Кроме того, на пласт могут воздействовать дополнительные внешние источники энергии, связанные с закачкой в пласт жидкости или газа для поддержания пластового давления или повышения эффективности вытеснения. Поэтому выделяют пять режимов разработки месторождений: 1) водонапорный или жёсткий водонапорный режим, когда нефть вытесняется в добывающие скважины под действием напора краевой или подошвенной воды. Для того, чтобы вода могла вытеснять нефть, необходимо подпитывать водоносный пласт поверхностной водой или осадками. Водонапорный режим можно создать искусственно, если закачивать воду в нагнетательные скважины. Схема проявления водонапорного режима показана на рисунке 1.7; 2) газонапорный режим, когда нефть или вода вытесняются в скважины под действием напора сжатого газа, находящегося в виде газовой шапки над нефтью или водой; иногда этот режим называют режимом газовой шапки; 3) режим растворенного газа возникает тогда, когда давление в нефтяной залежи падает ниже давления насыщения нефти газом. В этом случае газ из растворённого состояния переходит в свободное состояние (в виде пузырьков) и ,расширяясь, вытесняет нефть к забоям скважин. Такой режим правильней было бы назвать «режимом газированной жидкости»;
4) упругий водонапорный режим, при котором нефть поступает в скважины за счет упругих свойств жидкости и породы пласта. Схема проявления упругого водонапорного режима показана на рисунке 1.8. При снижении давления в пласте объём жидкость увеличивается, излишки жидкости вытесняются к скважинам. Это увеличение объёма незначительно, например, при снижении давления на 20 МПа объём воды увеличивается на один процент. Кроме того, при снижении давления в жидкости увеличивается нагрузка на скелет породы, это приводит к уменьшению пористости пласта и излишки жидкости также вытесняются к скважинам. Поэтому упругий водонапорный режим проявляется тогда, когда нефтяное месторождение окружено большими объёмами воды, т. е. радиус водоносной области Rв во много раз больше радиуса месторождения больше Rн. По своей природе этот режим нестационарный, то есть давление меняется с течением времени; 5) гравитационный режим, когда нефть или вода добываются из пласта только за счет силы тяжести самой нефти или воды. На гравитационном режиме работает Ярегское нефтяное месторождение в Республике Коми. В начальной стадии разработки этого месторождения в нефтяном пласте пробивались штреки, которые разбивали пласт на блоки. Под действием силы тяжести нефть из блоков вытекает в штреки. В связи с большой вязкостью нефти, коэффициент нефтеотдачи пласта при таком способе разработки составлял 5 — 8 процентов. В дальнейшем перешли к современным способам разработки с использованием горизонтально наклонных скважин и закачкой перегретого пара в пласт.
В промысловой практике нефтяная залежь редко эксплуатируется на каком–либо режиме весь период ее разработки. Так, месторождения с водонапорным режимом в начале разработки могут, вследствие высоких отборов нефти, перейти на режим растворенного газа или упругий водонапорный режим. Для практики разработки газовых и газоконденсатных месторождений характерны два режима разработки – газовый и водонапорный. При газовом режиме приток газа к добывающим скважинам происходит за счет расширения газа при снижении давления в залежи. При этом контурные или подошвенные воды практически не вторгаются в газовую залежь и, следовательно, объем порового пространства газовой залежи практически не изменяется по времени. При водонапорном режиме в процессе разработки в газовую залежь поступает контурная или подошвенная вода, что приводит к уменьшению объема порового пространства газовой залежи. При этом приток газа к забоям добывающих скважин осуществляется за счет напора воды, поступающей в газовую залежь.
Примеры и задачи Определить скорость фильтрации и действительная скорость движения газа у стенки гидродинамически совершенной скважины, если известно, что толщина пласта h = 10 м, коэффициент пористости m = 12%, радиус скважины rc = 0,1 м, массовый дебит газовой скважины Qm = 50 т/сут, плотность газа при атмосферном давлении (pат = 0,1013 МПа) r = 0,8 кг/м 3 . Абсолютное давление на скважине равно pс = 10 МПа. Массовый расход в системе СИ равен: Qm = 50 т/сут = 50·1000/86400 = 0,589 кг/с. По уравнению неразрывности потока при установившемся движении массовый расход в любом поперечном сечении потока одинаков. Поэтому массовый расход газа на боковой поверхности скважины будет равен: Плотность газа в этом поперечном сечении равна: rс = rат pc/pат = 0,8·10·10 6 /0,1013·10 6 = 80,0 кг/м 3 . Приток к скважине представляет собой плоскорадиальный поток, поэтому площадь поперечного сечения: w = 2 p rc h. Объемный расход на забое скважины связан с массовым расходом соотношением Qс = Qm/rс. Тогда скорость фильтрации будет определяться:
Действительная скорость движения нефти v = u/m = 1,17 10 -3 /0,12 = 9,77 10 -3 м/с. Ответ: u = 1,17 10 -3 м/с.; v = 9,77 10 -3 м/с. Вертикальная труба, содержащая пористую среду, заполнена водой. Верхний и нижний торец трубы открыт. Определить скорость фильтрации, если известно, что коэффициент проницаемости k = 0,2 мкм 2 , а динамическая вязкость и плотность воды m = 0,98 мПа·с; r = 1000 кг/м 3 . Выберем плоскость сравнения по нижнему торцу трубы. Длину трубы обозначим через L. Приведенные давления на верхнем и нижнем торце соответственно равны: Тогда по закону Дарси скорость фильтрации равна: Давление вокруг скважины в горизонтальном пласте распределяется по закону:
Определить скорости фильтрации и дебиты в двух точках: на самой скважине и на расстоянии 20 м от оси скважины, если известно, что коэффициент проницаемости k = 0,2 мкм 2 , динамическая вязкость нефти m = 20 мПа×с, толщина пласта h = 7 м. Радиус скважины и контура питания соответственно равны rc = 0,1 и Rк = 100 м. Давление на скважины и контуре питания: pc = 10 МПа и pк = 20 МПа. В горизонтальном пласте приведенное давление совпадает с абсолютным. По закону Дарси скорость фильтрации определяется:
Тогда скорости фильтрации будут равны:
Дебиты в данных сечениях будут равны: Q1 = u1 2 p r1 h = — 1,44×10 -4 ×2×3,14×0,1×7 = — 6,33×10 -4 м/с; Q2 = u2 2 p r2 h = — 0,72×10 -5 ×2×3,14×20×7 = — 6,33×10 -4 м 3 /с. Знак дебита отрицательный, так как вектор скорости направлен против выбранной оси – радиуса. Ответ: u1 = — 1,44×10 -4 м/с, u2 = — 0,72×10 -5 м/с, Q = — 6,33×10 -4 м 3 /с.
На рисунке 1.11 показана карта изобар в горизонтальном пласте. Определить скорость фильтрации в направлении вектора n1, если известно, что коэффициент проницаемости k = 0,250 мкм 2 , динамическая вязкость нефти m = 20 мПа×с. Давления на карте изобар – МПа. Выбираем две точки на двух ближайших изобарах вдоль вектора. Обозначим на них давление: p(s + Δs) = 17 МПа. Давление на изобаре, откуда выходит вектор: p(s) = 16 МПа. Находим расстояние между этими точками DS = 20 . По
закону Дарси скорость фильтрации u определяется: Знак скорости отрицательный, поэтому жидкость фильтруется в направлении обратном направлению стрелки. Ответ: uср = — 3,12×10 -7 м/с. Дебит газовой скважины, приведенный к атмосферному давлению при стандартных условиях: Qaт.ст = 2 млн. м 3 /сут; абсолютное давление на забое рс = 12 МПа, толщина пласта h = 10 м, коэффициент пористости пласта m = 12%, коэффициент проницаемости k = 0,5 мкм 2 , плотность газа при стандартных условиях rст = 0,750 кг/м 3 , динамический коэффициент вязкости в пластовых условиях m = 0,015 мПа×с, температура пласта 45°С. Определить, нарушается ли закону Дарси в призабойной зоне совершенной скважины радиусом гс = 0,10 м. Определим массовый дебит газа: Площадь поперечного сечения на забое скважины: Ответ: в призабойной зоне закон Дарси нарушается. Задачи к контрольной работе По керну диаметром 2 см, длиной 5 см за десять минут прокачано 0,6 см 3 воды. Абсолютное давление на входе 0,5 МПа, а на выходе 0,2 МПа. Определить действительную скорость и скорость фильтрации на входе в керн, если пористость керна 10%. По керну диаметром 2 см и длиной 5 см за десять минут прокачано 600 см 3 газа при стандартных условиях. Абсолютное давление на входе 0,5 МПа, а на выходе 0,3 МПа. Определить действительную скорость и скорость фильтрации на входе в керн, если пористость керна 10%. По керну диаметром 2 см, длиной 5 см за десять минут прокачано 600 см 3 газа при стандартных условиях. Абсолютное давление на входе 0,5 МПа, а на выходе 0,3 МПа. Определить действительную скорость и скорость фильтрации на выходе из керна, если пористость керна 10%. Нефтяная галерея в пласте толщиной 10 м за месяц дает 8000 тонн нефти плотностью 780 кг/м 3 . Ширина галерея 100 м, длина 300 м, пористость пласта 15%. Определить действительную скорость и скорость фильтрации на галерее. Газовая галерея в пласте толщиной 12 м за месяц дает 9000 тонн газа плотностью, при атмосферном давлении, 0,75 кг/м 3 . Ширина галерея 100 м, длина 300 м, пористость пласта 15%, давление на галерее pг = 4 МПа. Определить действительную скорость и скорость фильтрации на галерее. Газовая галерея в пласте толщиной 15 м за сутки дает 800 тыс. м 3 газа плотностью, при атмосферном давлении, 0,75 кг/м 3 . Ширина галерея 100 м, длина 300 м, пористость пласта 15%, давление на контуре питания pк = 8 МПа. Определить действительную скорость и скорость фильтрации на контуре питания. Нефтяная совершенная скважина радиусом 0,1 м в пласте толщиной 10 м за один час дает 2 м 3 нефти. Определить скорость фильтрации и действительную скорость на скважине, если пористость пласта 15%. Нефтяная скважина радиусом 0,1 м в пласте толщиной 8 м за 1 час дает 3 м 3 нефти и вскрывает пласт на 3 метра. Определить скорость фильтрации и действительную скорость на скважине, если пористость пласта 20%. Определить среднее значение скорости фильтрации на боковой поверхности гидродинамически несовершенной по характеру вскрытия нефтяной скважины, если толщина пласта h = 25 м, плотность перфорации nп = 10 отв/м с диаметром отверстий dп = 1 см, дебит жидкости Q = 250 м З /сут. За десять дней из скважины добыт объем газа (приведенный к атмосферному давлению и пластовой температуре) Vат = 15 млн м 3 , радиус контура питания rk = 200 м, толщина пласта h = 20 м, абсолютное давление газа на контуре pk = 15 МПа. Определить скорость фильтрации и действительную скорость газа на контуре питания. Определить скорость фильтрации и среднюю скорость движения при плоскорадиальной фильтрации газа к скважине в точке на расстоянии r = 150 м от центра скважины, если давление в этой точке равно р = 8 МПа, толщина пласта h = 12 м, пористость его m = 20%, а приведенный к атмосферному давлению и пластовой температуре дебит Qат = 2·10 6 м 3 /сут, pат = 0,1 МПа. Газовая скважина радиусом 0,1 м в пласте толщиной 20 м за сутки дает 80 тонн газа плотностью ρат = 0,8 кг/м 3 и вскрывает пласт на 3 метра. Скважина несовершенна по характеру вскрытия и её вскрытая часть имеет плотность перфорации nп = 10 отв/м с диаметром отверстий dп = 1 см. Определить скорость фильтрации и действительную скорость на скважине, если давление на скважине 10 МПа, пористость пласта 20%. Определить коэффициент пористости, зная, что действительная скорость движения через образец, определяемая при помощи индикатора, равна v = 5·l0 ‑3 см/с, коэффициент проницаемости k = 0,2 мкм 2 , вязкость жидкости μ = 4 мПа·с, разность давлений Dр = 2 МПа при длине образца L = 15 см. Указание: найти скорость фильтрации и сравнить с действительной скоростью. В нефтяной галерее давление распределяется по закону p(x) = ‑ (pk ‑ pг) x/L. Давление на контуре питания pк = 8 МПа, давление на галерее pг = 4 МПа, длина галереи 200 м, проницаемости пласта k = 1 мкм 2 , динамический коэффициент вязкости жидкости μ = 2 мПа·с. Определить скорость фильтрации на расстоянии x = 50 м от контура питания. В газовой галерее давление распределяется по закону p(x) 2 = pk 2 ‑ (pk 2 ‑ pг 2 ) x/L. Давление на контуре питания pк = 9 МПа, давление на галерее pг = 3 МПа, длина галереи 200 м, проницаемости пласта k = 0,1 мкм 2 , динамический коэффициент вязкости газа μ = 0,015 мПа·с. Определить скорость фильтрации на расстоянии x = 50 м от контура питания. Вокруг нефтяной скважины давление меняется по закону p(r) = pk ‑ (pk ‑ pc) ln(Rk/r)/ln(Rk/rc). Давление на контуре питания pк = 18 МПа, давление на скважине pс = 14 МПа, радиус контура питания 100 м, проницаемости пласта k = 0,3 мкм 2 , динамический коэффициент вязкости нефти μ = 6,28 мПа·с. Определить скорость фильтрации на расстоянии r = 10 м от скважины. Вокруг газовой скважины давление меняется по закону p 2 (r) = p 2 c + (p 2 k ‑ p 2 c) ln(r/rc)/ln(Rk/rc). Давление на контуре питания pк = 12 МПа, давление на скважине pс = 6 МПа, радиус контура питания 100 м, проницаемости пласта k = 0,4 мкм 2 , динамический коэффициент вязкости газа μ = 0,02 мПа·с. Определить скорость фильтрации на расстоянии r = 1 м от скважины. Модель пласта представляет собой трубу диаметром 200 мм и длиной 2 м, заполненную песком. Труба установлена вертикально. На верхнем конце модели поддерживается манометрическое давление 30 кПа, а нижний конец модели открыт. Определить скорость фильтрации и расход воды, если проницаемости модели k = 0,4 мкм 2 , динамический коэффициент вязкости воды μ = 1 мПа·с.
Определить величину и направление скорости фильтрации в точке А (рисунок 1.12), если проницаемость пласта равна 0,12 мкм 2 , а вязкость нефти 15 мПа·с. Нарисовать вектор скоростей. Указание: найти скорости фильтрации вдоль осей x и y. Определить величину и направление скорости фильтрации в точке B (рисунок 1.12), если проницаемость пласта равна 0,15 мкм 2 , а вязкость нефти 15 мПа·с. Нарисовать вектор скоростей. Указание: найти скорости фильтрации вдоль осей x и y. Определить величину и направление скорости фильтрации в точке C (рисунок 1.12), если проницаемость пласта равна 0,16 мкм 2 , а вязкость нефти 15 мПа·с. Нарисовать вектор скоростей. Указание: найти скорости фильтрации вдоль осей x и y. Определить приведенное относительно ВНК (водонефтяного контакта) давление в трех наблюдательных скважинах. Манометрические давления в скважинах pм1 = 18,3 МПа; pм2 = 18,7 МПа; pм3 = 17,3 МПа. Глубины спуска манометров H1 = 2180 м, H2 = 2280 м, H3 = 2020 м. Водонефтяной контакт находится на глубине 2320 м. Укажите направление скоростей фильтрации между скважинами. Плотность нефти принять равной 750 кг/м 3 . Вокруг двух скважин приведенное давление меняется по закону p(x,y) = pk + Dp1 ln((x – a) 2 + y 2 ) + Dp2 ln((x + a) 2 + y 2 ) . Определить скорость фильтрации в точке с координатами x = 20 м, y = 100 м, если Dp1 = Dp2 = 2,6 МПа; a = 100 м, проницаемость пласта 0,4 мкм 2 , динамический коэффициент вязкости нефти μ = 22 мПа·с. Вокруг двух скважин приведенное давление меняется по закону p(x,y) = pk + Dp1 ln((x – a) 2 + y 2 ) + Dp2 ln((x + a) 2 + y 2 ) . Определить скорость фильтрации в точке с координатами x = 20 м, y = 100 м, если Dp1 = 4,5 МПа; Dp2 = — 4,5 МПа; a = 100 м, проницаемость пласта 0,24 мкм 2 , динамический коэффициент вязкости нефти μ = 12 мПа·с. Определить значение числа Рейнольдса у стенки гидродинамически несовершенной по характеру вскрытия нефтяной скважины, если известно, что эксплуатационная колонна перфорирована, на каждом погонном метре колонны прострелено 10 отверстий диаметром dп = 10 мм, толщина пласта h = 15 м, проницаемость пласта k = 0,15 мкм 2 , пористость его m = 18%, коэффициент вязкости нефти μ = 4 мПа·с, плотность нефти ρ = 870 кг/м 3 и дебит скважины составляет 140 м 3 /сут. 📺 ВидеоЗакон БернуллиСкачать  Основное уравнение динамики вращательного движения. 10 класс.Скачать  Первая основная задача динамики. Задачи 1, 2, 3, 4Скачать  Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать  Подземная гидромеханика Лекция 9 Ильдар ИбрагимовСкачать  Парадокс сужающейся трубыСкачать  лекция 6 гидромеханика веснаСкачать  Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать  Порядок построения траектории скважины / Основы ННБСкачать  Щелевой или сетчатый фильтр / Какой Фильтра сделать и устанавить в скважинуСкачать  Метод узловых потенциалов. Самое простое и понятное объяснение этого методаСкачать  Гидродинамика. Вывод уравнения БернуллиСкачать  Дифференциальные уравнения движения материальной точки. Часть 1Скачать  Найти общее решение уравнения в частных производных первого порядка.Скачать  Дифференциальное уравнение Лагранжа II рода. Расчет механической системы.Скачать  Водопонижение безнапорная совершенная схема: метод большого колодца. Дюпуи.Скачать  Почему мы используем именно свои ЩЕЛЕВЫЕ ФИЛЬТРЫ? Трубы нПВХ для скважин.Скачать  Как победить гидроудары при работе скважинного насоса? Почему скважина может начать песочить?Скачать  |
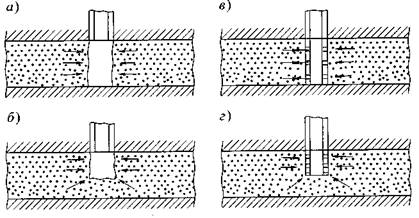
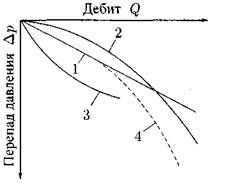
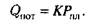
Рисунок 1.8 – Схема к упругому водонапорному режиму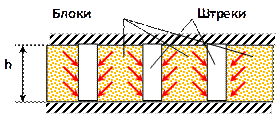
Схема к гравитационному режиму
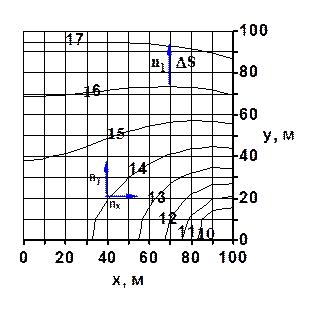Карта изобар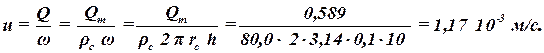
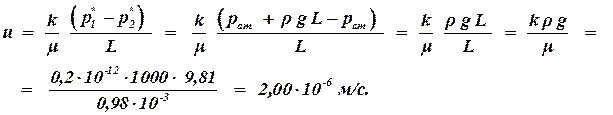Ответ: u = 2,00×10 -6 м/с.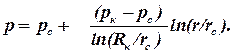
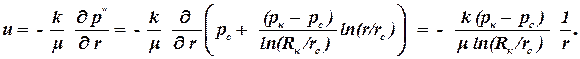
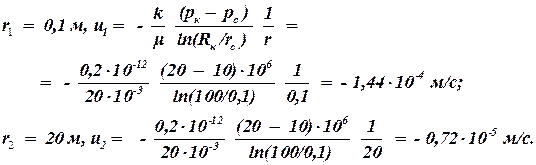
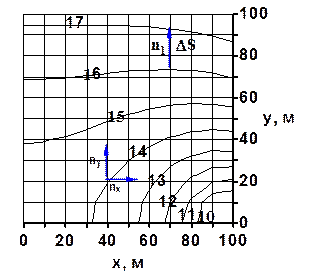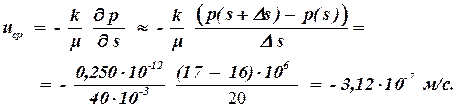
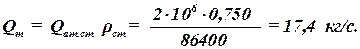
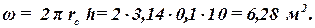
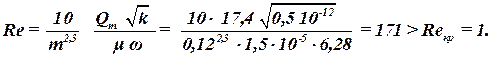
Рисунок 1.11 – Карта изобар
Карта изобар