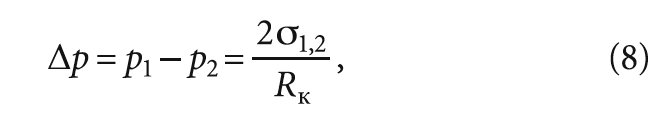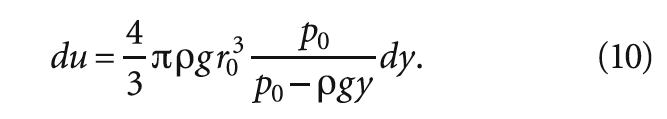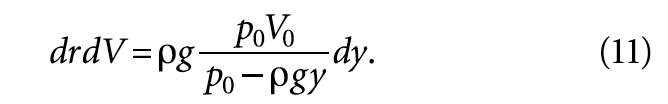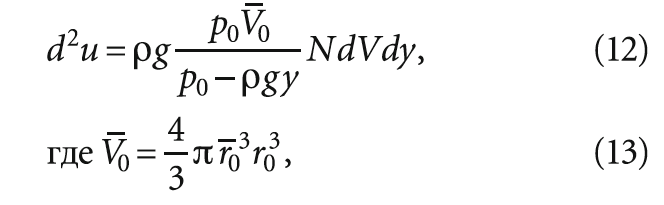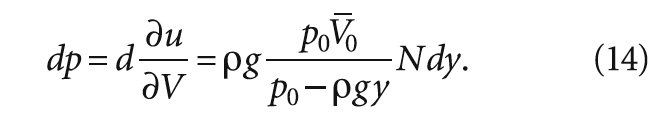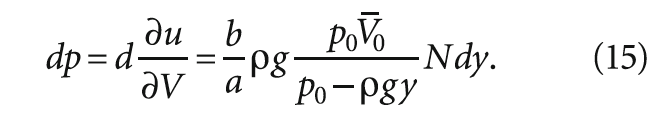Твердая частичка или жидкая капелька, движущаяся под действием силы тяжести сквозь вязкую жидкость, в конечном счете приобретает постоянную скорость. Она называется скоростью осаждения. Если плотность частицы ниже, чем плотность жидкости, она будет двигаться вверх со скоростью всплытия. Эти скорости обозначаются буквами vg (g – сила тяжести). Величина скорости осаждения/всплытия определяется следующими физическими параметрами:
•диаметром частицы d, м
•плотностью частицы ρp, кг/м3
•плотностью непрерывной фазы, ρl, кг/м3
•вязкостью непрерывной фазы η, кг/м,с
•ускорением силы тяжести g = 9,81 м/с2.
Если известны значения всех вышеперечисленных параметров, то можно рассчитать скорость осаждения/всплытия частицы или капли при помощи следующей формулы, выведенной из закона Стокса (формула 1):

Подставляем эти значения в формулу получим:
Как видим из полученного результата, жировые шарики поднимаются очень медленно. На практике шарики жира образуют крупные скопления и их всплытие происходит гораздо быстрее.
Периодическое сепарирование под действием силы тяжести
Рисунок 1
В сосуде А, показанном на рис. 1, содержится жидкость, в которой во взвешенном состоянии находятся твердые частицы одинаковых размеров и более плотные, чем жидкость. Для того чтобы находящиеся на поверхности жидкости частицы опустились на дно, должно пройти довольно много времени.
Время осаждения может быть сокращено при условии сокращения этой дистанции. Высоту сосуда (В) уменьшили, а площадь увеличили с тем, чтобы объем остался неизменным. Дистанция осаждения (h2) уменьшилась до 1/5 от первого варианта (h), и время, требуемое для полного разделения фракций, так же сократилось до 15 (рисунок 2).
Рисунок 2
Непрерывное сепарирование под действием силы тяжести
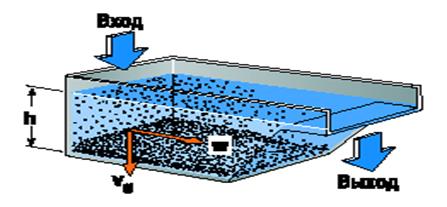
Простейший сосуд, в котором может осуществляться непрерывное отделение частичек разного диаметра от жидкости, показан на рис. 3. Жидкость, содержащая частички в виде шлама, поступает в сосуд с одного его конца и движется в направлении выхода на другом конце под определенным напором. При движении частички оседают с различной скоростью в зависимости от их диаметров.
Рисунок 3
При непрерывном отделении взвеси от жидкости в сосуде с горизонтальными экранами осадительные каналы будут постоянно забиваться собирающимися в них частицами. В конце концов процесс остановится. В сосуде с наклонными экранами, показанном на рис. 4, частицы, оседающие на экранах, соскальзывают под действием силы тяжести с экранов и скапливаются на дне сосуда.
Рисунок 4
Почему частицы, оседающие на экранах, не захватываются жидкостью, текущей вверх между экранами? Объяснение дано на рис. 5, на котором
показан разрез части осадительного канала. Когда жидкость течет между экранами, ее пограничный слой, ближайший к экранам, тормозится трением, и поэтому скорость его падает до нуля. Стационарный пограничный слой оказывает тормозящее воздействие на соседний слой, и так далее в направлении к центру канала, где скорость максимальная.
Рисунок 5
Получается профиль скоростей, как показано на рисунке 5, – ламинарный поток в канале. Частицы, осевшие в стационарной пограничной зоне, таким образом, находятся под воздействием только силы тяжести.
Поверхность для осаждения, используемая при прохождении через сосуд с наклонными вставками максимального потока, должна быть предварительно рассчитана. Для полного использования пропускной способности разделительного сосуда необходимо предоставить оседающим частицам как можно большую поверхность. Расстояние, в пределах которого происходит осаждение, не оказывает непосредственного влияния на пропускную способность сосуда, но какую-то минимальную ширину канала необходимо выдерживать, чтобы не допустить забивания каналов оседающими частицами.
Видео:Изучение принципа действия сепаратора-сливкоотделителяСкачать

Технико – технологические способы обезвоживания и обессоливания нефтей
Читайте также:
|
| Обводнённость | 1 % | 5 % | 10 % | 15 % | 20 % | 30 % |
 , мкм , мкм |
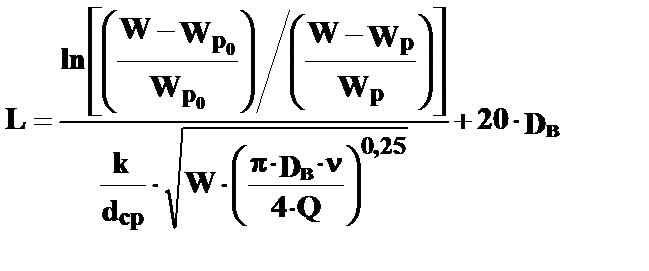
где: 


К – константа эффиктивности столкновений;


К достоинствам трубчатых коалесценторов можно отнести их промтоту и возможность одновременного использования в качестве коммуникационных линий.
Принципиальные схемы трубчатых гидродинамических каплеобразователей приведены на рис. 72.

Рис.72. Принципиальные схемы трубчатых гидродинамических каплеобразователей
Электрокоалесценторы не нашли пока широкого распространения в нефтяной промышленности, в основном, из – за ограничения содержания воды в исходной эмульсии 10 % об.;в виду опасности возникновения короткого замыкания в электрической цепи.
Принцип работы подобных аппаратов аналогичен работе электродегидраторов, рассмотренных ниже.
Разрушение водо – нефтяных эмульсий в центрифуге
Водо – нефтяная эмульсия подаётся в центрифугу по её оси. Внутри центрифуги размещается быстро вращающийся направляющий набор стальных пластин, придающий ей круговое движение. Благодаря центробежной силе вода и сухие порошки, как более тяжелые субстанции, стремятся выйти из связанного состояния, концентрируясь (а для воды и укрупняясь) вдоль стенок, постепенно стекая вниз. Обезвоженная нефть (и обессоленная), лишенная механических примесей, отводится по самостоятельным трубам с верхней части аппарата. Водная смесь отводится с нижней части аппарата.
Предельный диаметр глобул, осаждаемых в центрифуге, может быть определён по уравнению Стокса:
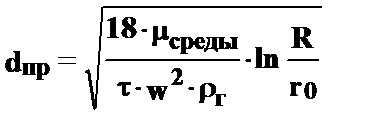


w – угловая скорость :

n – число оборотов центрифуги;
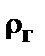
R — максимальный радиус вращения эмульсии в центрифуге;
Данный способ обезвоживания, не смотря на свою высокую эффективность, ввиду большой стоимости, сложности и очень низкой производительности на промыслах, практически не применяется.
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.017 сек.)
Видео:Как производятся круги Gtool на липучке. Станок для производства Velcro кругов.Скачать

Теоретические исследования движения пузырьков воздуха в потоке воды при аэрации
УДК 628.16. Научная специальность: 05.23.04.
Теоретические исследования движения пузырьков воздуха в потоке воды при аэрации
В. Б. Викулина, к.т.н., доцент; Л. В. Инешина, студентка бакалавриата, Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ)
Аэрационные сооружения, используемые в очистке воды, требуют оптимизации технологического процесса по признакам формирования и распределения воздушных масс в потоке водоочистного сооружения. В качестве транспортного потока в водоочистных сооружениях используется вода, поэтому это обстоятельство позволяет использовать законы гидродинамики потока при всплытии пузырьков воздуха в качестве дополнительного фактора. В статье приводятся физические принципы всплытия пузырьков воздуха при аэрации. Теоретически обосновывается всплывание пузырьков воздуха в статических условиях жидкости и динамических условиях потока. Получена теоретическая зависимость, которая направлена на нормализацию неустойчивости работы аэрационных сооружений и на определение оптимальных условий технологического процесса.
Ключевые слова: аэрация, пузырёк воздуха, вязкость динамическая, скорость потока, граница раздела фаз, распределение скоростей.
UDC 628.16. The number of scientific speciality: 05.23.04.
Theoretical studies of the motion of air bubbles in the water flow during aeration
V. B. Vikulina, PhD, Associate Professor; L. V. Inesina, undergraduate student, Moscow State University of Civil Engineering (MGSU)
Aeration facilities used in water treatment require optimization of the technological process on the basis of the formation and distribution of air masses in the flow of the water treatment plant. Water is used as a transport flow in water treatment facilities, so this circumstance allows to use the laws of flow hydrodynamics at the ascent of air bubbles as an additional factor. Physical principles of air bubbles ascent during aeration are given. Theoretically justified the rise of air bubbles in static fluid conditions and dynamic flow conditions. The obtained theoretical dependence, which is aimed at the normalization of instability of operation of the aeration structures and the determination of optimal process conditions.
Keywords: aeration, air bubble, dynamic viscosity, flow rate, phase boundary, velocity distribution.
Аэрационные сооружения, используемые в очистке воды, требуют оптимизации технологического процесса по признакам формирования и распределения воздушных масс в потоке водоочистного сооружения. В качестве транспортного потока в водоочистных сооружениях используется вода, поэтому это обстоятельство позволяет использовать законы гидродинамики потока при всплытии пузырьков воздуха в качестве дополнительного фактора. В статье приводятся физические принципы всплытия пузырьков воздуха при аэрации. Теоретически обосновывается всплывание пузырьков воздуха в статических условиях жидкости и динамических условиях потока. Получена теоретическая зависимость, которая направлена на нормализацию неустойчивости работы аэрационных сооружений и на определение оптимальных условий технологического процесса.
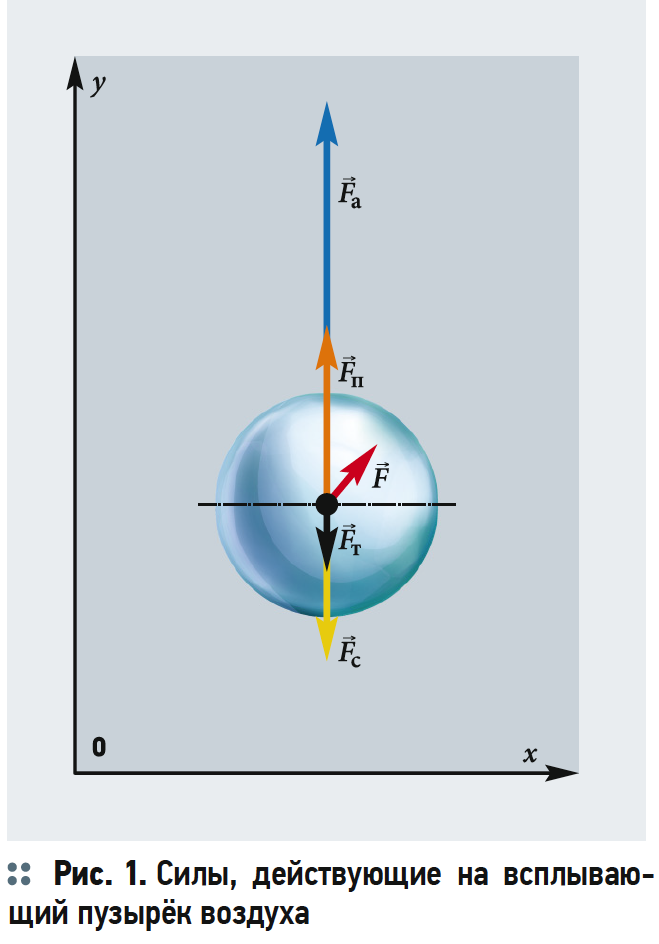
Движение потоков в сооружениях водоочистки с аэрацией (например, аэротенк, аэрофильтр, аэрируемая песколовка) создают технологическую особенность. Основным процессом, в физическом понимании аэрации, является движение пузырьков воздуха снизу вверх. Рассмотрим всплывание пузырька воздуха в жидкости, находящейся в состоянии покоя.
Предположим, что пузырёк воздуха в жидкости имеет форму шара [1].
На всплывающий пузырёк действуют три силы: сила тяжести Fт, архимедова сила Fа и сила сопротивления Fc (рис. 1). В проекции на вертикальную ось OY подъёмная сила Fп равна:
Силы выражаются в ньютонах (Н).
Рассмотрим действие сил при равномерном движении пузырька в воде.
Сила Архимеда (выталкивающая сила) приводит пузырёк в движение вверх, при этом диаметр пузырька увеличивается, достигая своего максимума на поверхности воды.
Сила Стокса (сила трения) при движении пузырька действует в направлении, противоположном силе Архимеда, и направлена сверху вниз.
Сила тяжести действует в условиях ускорения свободного падения и направлена сверху вниз.
Сила Стокса возникает в результате взаимодействия жидкости с пузырьком и равна силе трения, на преодоление которой затрачивается работа.
Разность энергий двух состояний пузырька до начала совершения работы и после — это работа как избыточная свободная энергия. С точки зрения гидростатики дополнительная потенциальная энергия равносильна динамическому напору.
При условии сжимаемости воздуха и при движении пузырька вверх наружное давление на стенки пузырька будет меняться с высотой, а диаметр пузырька будет увеличиваться. Расширение воздуха в пузырьке может происходить либо изотермически, либо адиабатически. Поскольку размер пузырька определяют условия гидростатики и силы Стокса, то принимаем расширение воздуха в пузырьке как изотермическое, поэтому размеры пузырька должны быть достаточно малыми.
Запишем условие для изотермического процесса при вертикальном всплытии пузырька воздуха:
где p — давление жидкости, Па; V — объём жидкости, м³.
Если p0 — атмосферное давление [Па], то давление на глубине h [м] в жидкости плотностью ρ [кг/м³] будет равно (p0 + ρgh), где g — ускорение свободного падения, g = 9,81 м/с2; ρ — плотность жидкости, кг/м³; h — глубина, м.
Согласно закону изотермического расширения пузырька (2) на глубине слоя жидкости найдём радиус пузырька:
где r0 — радиус пузырька на поверхности воды, мм.
Пузырёк движется со скоростью v в жидкости, характеризуемой динамической вязкостью [Па·с]. Движение сферического пузырька в жидкости, которая рассматривается как непрерывная среда, и размеры которого (пузырька) значительно превышают размеры молекул среды, описывается уравнением Стокса для вязкого сопротивления:
где Fc — сила Стокса, Па; м — динамическая вязкость, Па·с или Н·с/м²; v — скорость всплытия пузырька, м/с.
Сила Архимеда Fа (подъёмная сила для пузырька) определяется из выражения
и она равна силе Стокса.
Сила тяжести равна:
где m — масса пузырька, кг.
Сила тяжести зависит от геометрических размеров пузырька. Эта сила крайне мала в сравнении с силами, действующими на пузырёк воздуха в воде, следовательно, значением силы тяжести можно пренебречь.
Скорость всплывания пузырька находится по уравнению:
От шарообразной формы переходим к изменению форм пузырька [2, 3].
Пузырёк находится в движении во время подъёма до поверхности воды. При этом пузырёк воздуха принимает шарообразную форму за счёт действия сил поверхностного натяжения.
Кроме того, изменение давлений сред (внутренней и внешней) пузырька приводит к деформации его поверхности, что способствует колебанию пузырька.
Применительно к единичному всплывающему пузырьку, на границе раздела фаз возникает разность давлений Δр, описываемая уравнением:
где р1 и р2 — давления двух фаз на глубине, Па; σ1,2 — поверхностное натяжение на границе двух фаз, Н/м; Rк — радиус кривизны поверхности рассматриваемого пузырька, м.
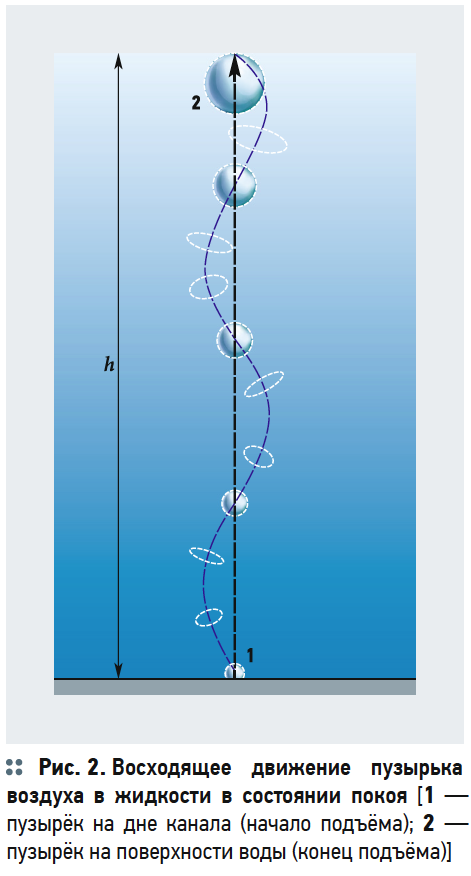
В результате увеличения объёма и изменения формы пузырька возникают его колебательные движения. Траектория всплытия пузырька принимается смещающейся относительно вертикали и носит волновой характер (рис. 2).
Теперь известны все величины, определяющие силу Стокса, что позволяет вычислить работу, совершаемую всплывающим пузырьком.
Вертикальное направление всплывания пузырька выберем за ось Oy.
Увеличение размеров и изменение формы пузырька передаётся окружающей пузырёк жидкости. Тем самым возникает суммарная работа dA и приращение свободной энергии согласно силам, действующим на пузырёк (рис. 1).
Поэтому приращение свободной энергии du в пересчёте на один пузырёк определится равенством:
где du и dA выражаются в джоулях (Дж).
Используя в формуле (9) выражения для силы Стокса (4), радиуса пузырька (3) и скорости всплытия пузырька (7), получаем следующий результат:
Для расчёта свободной энергии пузырьков введём функцию распределения f (r), которая представляет собой плотность вероятности обнаружения размера пузырька в единичном объёме между пузырьками с радиусами r и (r + dr).
Количество пузырьков с такими размерами в объёме dV будет равно f (r)drdV, поэтому их вклад в свободную энергию запишется как:
Помня, что V0 = 4/3(πr0 3 ), и интегрируя по всем возможным размерам пузырьков, получаем:
здесь r_ 03 — среднее значение куба радиуса пузырька на уровне поверхности жидкости, мм³; количество пузырьков в единице объёма жидкости, шт.
Термодинамическая связь параметров системы определяет давление р в системе как производную свободной энергии по объёму. Избыточное давления жидкости тогда составит:
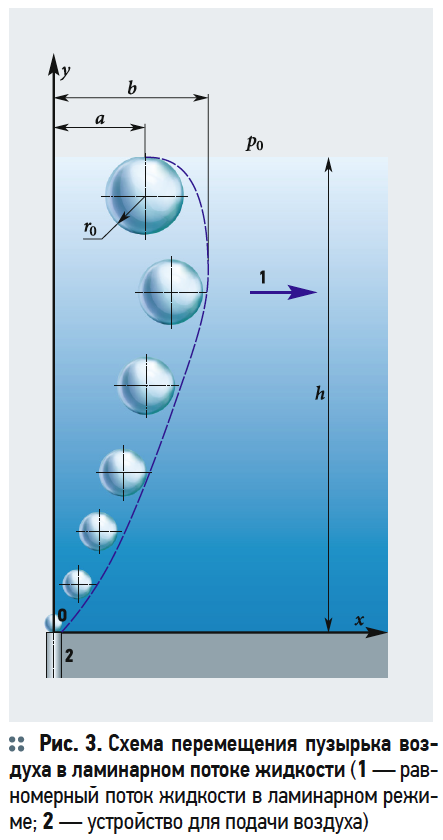
Рассмотрим всплытие пузырька воздуха в потоке жидкости при ламинарном режиме течения.
На рис. 3 представлена схема воздействие потока жидкости на вертикальное всплывание пузырька воздуха. Под воздействием распределения скоростей потока v = f(h) происходит смещение пузырька от вертикальной оси Oy. Согласно основным законам гидродинамики распределение скоростей зависит от кинетической энергии потока [3, 4]. По сечению потока происходит распределение скоростей, которые зависят от сопротивления между слоями жидкости при движении.
Нижние слои потока имеют сопротивление движению за счёт шероховатости дна, а движение верхнего слоя замедляется на границе раздела фаз «вода-воздух».
Обозначим через a [мм] расстояние от оси Oy до всплывшего пузырька на поверхности жидкости, а через b [мм] расстояние от оси Oy до всплывающего пузырька, максимально сместившегося по направлению движения жидкости.
Разница между a и b всплывающего пузырька зависит от скорости потока. Тогда выражение (14) запишется как
Полученная математическая зависимость позволяет более точно осуществить численные эксперименты на определённом этапе проектирования аэрационных сооружений систем водоочистки.
Эти действия направлены на нормализацию неустойчивости работы аэрационных сооружений и на определение оптимальных условий технологического процесса.
Выводы
1. Произведён анализ воздействия физических факторов на движение пузырька воздуха в воде, основанный на изотермическом процессе.
2. Получено уравнение, в котором приводится термодинамическая связь в определении давления в системе, как производная свободной энергии в потоке воды с учётом гидродинамических отклонений.
3. Использование полученного выражения позволяет повысить эффективность процесса водоочистки с применением аэрации.
📽️ Видео
Сепараторы для АЭС "Аккую" Horizontal moisture separator-reheater for AKKUYU Nuclear Power PlantСкачать

Cream separator ПеноотделительСкачать

Свой сепараторСкачать

Нормализация молокаСкачать

Сломанный сепаратор или меняем проводкуСкачать

ЦентрифугированиеСкачать

Как отрегулировать жирность сливок на любом сепараторе!Скачать

Сепараторы в молочной промышленностиСкачать

2021 10 29 Numerical methods in continuum mechanics CMCM 2021Скачать

БЮДЖЕТНЫЙ СЕПАРАТОР ДЛЯ КОЗЬЕГО МОЛОКА НЕПТУНСкачать

Cream separator ПеноотделительСкачать

Сепарирование молока. Как сепарировать молоко.СЕПАРАЦИЯ МОЛОКА. КАК СОБРАТЬ СЕПАРАТОР.Осень 2022г.Скачать

Сепарирую молоко, сколько сливок на выходе...Скачать

Обзор и сборка сепаратора. ИЗ ГОРОДА В ДЕРЕВНЮ 🏡Скачать

Рецепт молочых сливок СЕПАРАТОР ДЛЯ МОЛОКА. Обезжиривание молока в домашних условиях.Скачать

Сборка сепаратора Мотор Сич 100.15. Первое сепарирование молока новым сепаратором.Скачать

Работающий сепаратор молокаСкачать








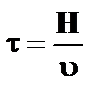 (29)
(29) — скорость седиментации.
— скорость седиментации. (30)
(30)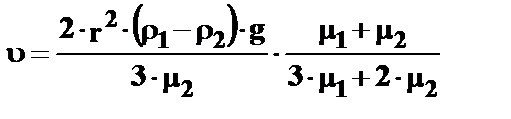 (31)
(31)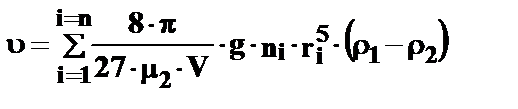 (32)
(32) — число частиц i-го размера.
— число частиц i-го размера.

 (33)
(33) — диаметр глобул пластовой воды;
— диаметр глобул пластовой воды;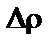 — разность плотностей воды и нефти;
— разность плотностей воды и нефти;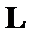 — длина аппарата;
— длина аппарата; — радиус аппарата;
— радиус аппарата; — высота водяной подушки;
— высота водяной подушки; (34)
(34)
 — поверхностное натяжение на границе нефть – вода (дин/см);
— поверхностное натяжение на границе нефть – вода (дин/см);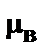 ,
, 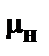 — динамическая вязкость воды и нефти соответственно, Па . с;
— динамическая вязкость воды и нефти соответственно, Па . с;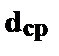 — средний диаметр капель воды, принимаемый согласно нижеприведённой таблицы, см;
— средний диаметр капель воды, принимаемый согласно нижеприведённой таблицы, см;
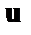 — средняя объёмная скорость потока, см 3 /с;
— средняя объёмная скорость потока, см 3 /с; — плотност3,, !*;ь нефти, г/см 3 .
— плотност3,, !*;ь нефти, г/см 3 .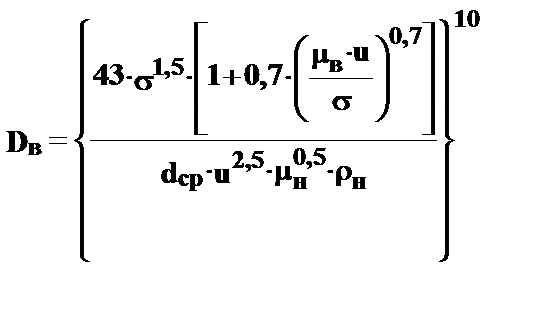 (35)
(35)