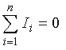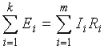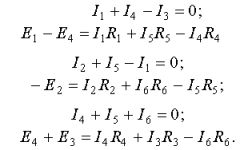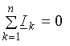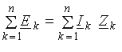Законы Кирхгофа — формулы и примеры использования

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

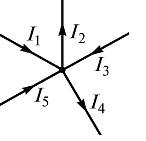
где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0

В этом уравнении токи, направленные к узлу, приняты положительными.

Физически первый закон Кирхгофа – это закон непрерывности электрического тока.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii , Ri – ток и сопротивление i -й ветви.

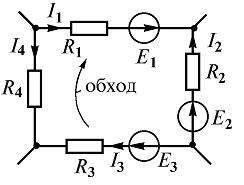
Так, для замкнутого контура схемы (рис. 2 ) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4

Замечание о знаках полученного уравнения:

1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;

2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.

Расчет разветвленной электрической цепи с помощью законов Кирхгофа

Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.

Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b , следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.

Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.

Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b — (y — 1) = b — y +1 .

Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.

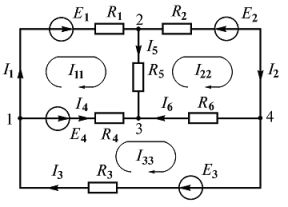
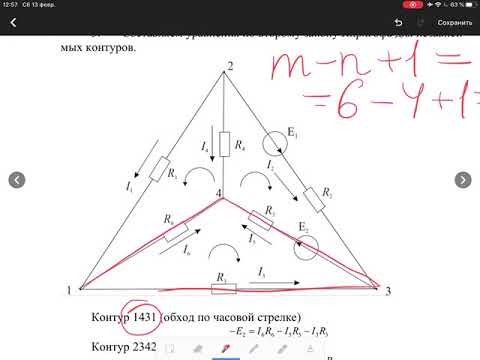
Составим систему уравнений Кирхгофа для электрической цепи (рис. 3 ). Схема содержит четыре узла и шесть ветвей.

Поэтому по первому закону Кирхгофа составим y — 1 = 4 — 1 = 3 уравнения, а по второму b — y + 1 = 6 — 4 + 1 = 3 , также три уравнения.

Произвольно выберем положительные направления токов во всех ветвях (рис. 4 ). Направление обхода контуров выбираем по часовой стрелке.

Составляем необходимое число уравнений по первому и второму законам Кирхгофа

Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.

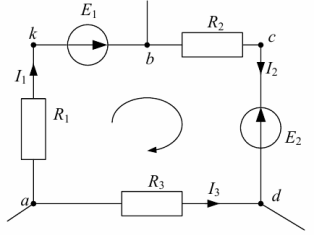
Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.

Рис. 4. Контур для построения потенциальной диаграммы

Потенциал любого узла принимаем равным нулю (например, ?а= 0), выбираем обход контура и определяем потенциалы точек контура: ?а = 0, ?к = ?а — I1R1 , ? b = ? к + Е1, ?с = ? b — I2R2 , ? d = ?c — Е2, ? a = ?d + I3R3 = 0

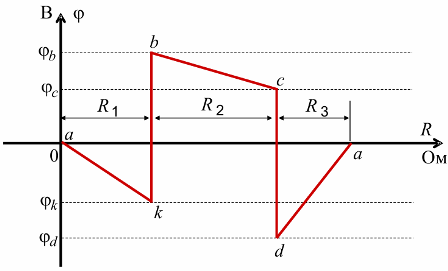
При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5 ).

Рис. 5. Потенциальная диаграмма

Законы Кирхгофа в комплексной форме

Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.

Первый закон Кирхгофа : «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»

Второй закон Кирхгофа : «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Не пропустите обновления, подпишитесь на наши соцсети:

Видео:Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Алгоритм составления уравнений

Алгоритм составления уравнений по законом Кирхгофа:

Видео:Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Составляем уравнения по первому закону Кирхгофа

Для составления уравнений по первому закону кирхгофа любой электрической цепи выполняем следующие действия.

1. Количество уравнений по 1 закону киргофа равно количеству узлов минус один.
2. Произвольно задаемся направлением токов в каждой ветви электрической цепи.
3. Если в ветви присутствует источник тока, то считаем данный ток уже известным, равным величине источника тока.
4. Составляем уравнения по первому правилу Кирхгофа для любых узлов кроме одного.
5. Расставляем знаки. Токи, которые втекают в узел берем с одним знаком, например с плюсом. Токи, которые вытекают из узла берем с противоположным знаком, например с минусом.

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Составляем уравнения по второму закону Кирхгофа

Для составления системы уравнения по 2 правилу Кирхгофа необходимо выполнить следующие пункты.

1. Количество уравнений по второму закону Киргофа равно количеству независимых контуров. По второму закону можно записать В-В_I-У+1 независимых уравнений. Где В — число ветвей в схеме. В_I— число ветвей в схеме с источником тока. У — число узлов в схеме.
2. Находим независимые контура в электрической цепи (чтобы отличались хотя бы одной ветвью).
3. Если в цепи присутствуют источники тока, то данные ветви не учитываем при нахождении независимых контуров.
4. Задаемся произвольным направление обхода независимых контуров.
5. Составляем уравнения по второму правилу Кирхгофа для каждого выбранного контура.
6. Расставляем знаки на участках с нагрузкой. Если направление обхода контура совпадает с направлением протекающего тока, то падение напряжения на заданном участке берем со знаком «+». Если направление протекающего тока не совпадает с направлением обхода контура, то падение напряжения на данном участке берем со знаком «-«.
7. Расставляем знаки на участках с источниками ЭДС. Если направление действия ЭДС (направление стрелочки) совпадает с направлением обхода независимого контура, то знак будет «плюс». Если не совпадает, то знак — «минус».

Видео:Законы Кирхгофа - самое простое и понятное объяснение этих законовСкачать

Расчет токов по правилам Кирхгофа

Полученные уравнения объединяем в систему уравнений. Количество уравнений должно быть равно количеству неизвестных. Далее решаем систему уравнений любым известным способом.

Правильность расчета проверяется составлением уравнения баланса мощностей.

Видео:решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

Законы Кирхгофа для расчёта электрических цепей

При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.

Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.

Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.

Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза [1].

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:

или в комплексной форме

Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:

Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно $ N_textrm-1 $, где $ N_textrm $ – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно $ N_textrm-N_textrm+1 $, где $ N_textrm $ – число ветвей. Количество составляемых уравнений по второму закону Кирхгофа легко определить по виду схемы: для этого достаточно посчитать число «окошек» схемы, но с одним уточнением: следует помнить, что контур с источником тока не рассматривается.

Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.

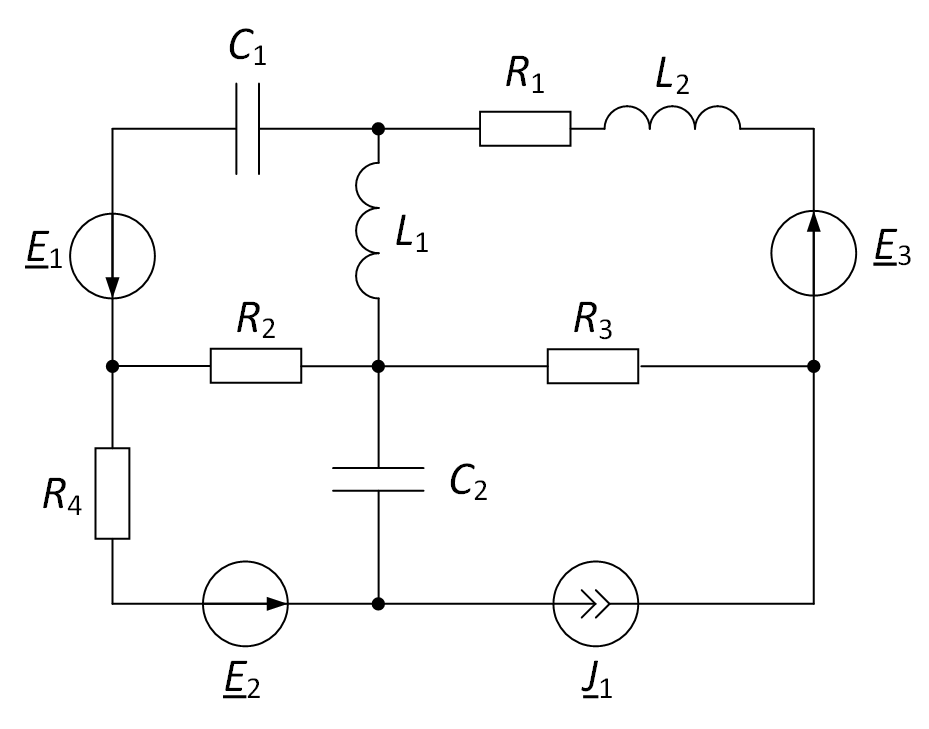
Рис. 1. Рассматриваемая электрическая цепь

Для начала необходимо задать произвольно направления токов в ветвях и задать направления обхода контуров (рис. 2).

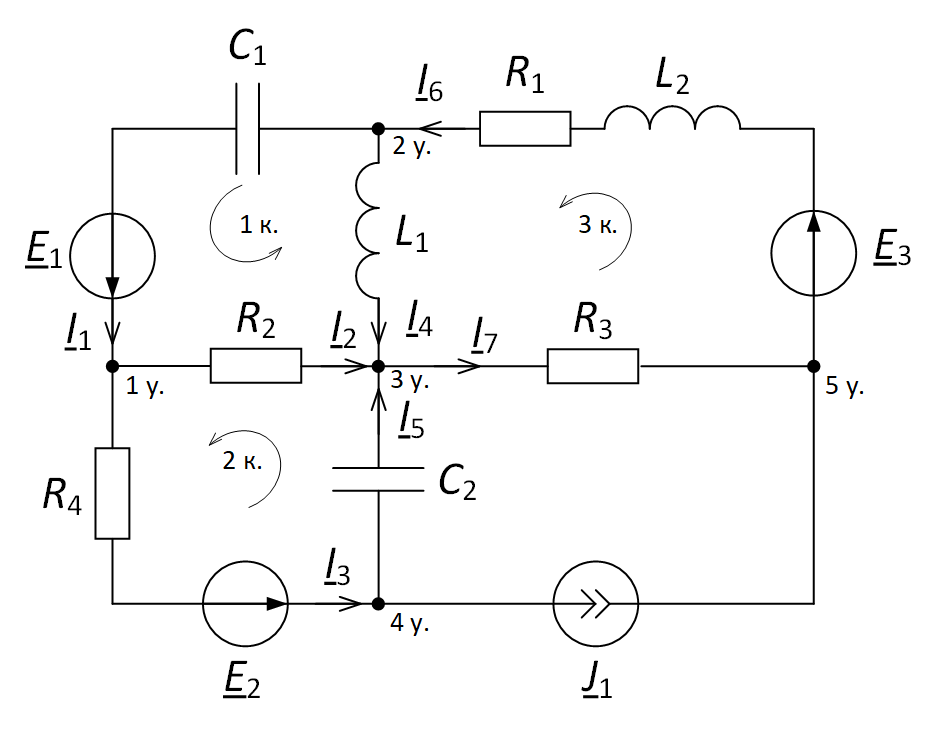
Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи

Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4. Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока $ underline_ $, не рассматривается.

Составим уравнения по первому закону Кирхгофа. Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

$$ underline_- underline_- underline_ = 0; $$

для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

$$ -underline_- underline_ + underline_ = 0; $$

$$ underline_+ underline_ + underline_- underline_ = 0; $$

$$ underline_- underline_- underline_ = 0. $$

Уравнение для узла «5 у.» можно не составлять.

Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

$$ underline_ cdot underline_ + R_ cdot underline_- underline_ cdot underline_ = underline_; $$

для контура «2 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

$$ -R_ cdot underline_ + R_ cdot underline_ + underline_ cdot underline_ = underline_; $$

для контура «3 к.»:

$$ underline_ cdot underline_ + (underline_ + R_) cdot underline_ + R_ cdot underline_ = underline_; $$

где $ underline_ = -frac $, $ underline_ = omega L $.

Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:

$$ begin underline_- underline_- underline_ = 0 \ -underline_- underline_ + underline_ = 0 \ underline_+ underline_ + underline_- underline_ = 0 \ underline_- underline_- underline_ = 0 \ underline_ cdot underline_ + R_ cdot underline_- underline_ cdot underline_ = underline_ \ -R_ cdot underline_ + R_ cdot underline_ + underline_ cdot underline_ = underline_ \ underline_ cdot underline_ + (underline_ + R_) cdot underline_ + R_ cdot underline_ = underline_ end $$

В данном случае это система из 7 уравнений с 7 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:

$$ begin 1 & -1 & -1 & 0 & 0 & 0 & 0 \ -1 & 0 & 0 & -1 & 0 & 1 & 0 \ 0 & 1 & 0 & 1 & 1 & 0 & -1 \ 0 & 0 & 1 & 0 & -1 & 0 & 0 \ underline_ & R_ & 0 & -underline_ & 0 & 0 & 0 \ 0 & -R_ & R_ & 0 & underline_ & 0 & 0 \ 0 & 0 & 0 & underline_ & 0 & R_+underline_ & R_ \ end cdot begin underline_ \ underline_ \ underline_ \ underline_ \ underline_ \ underline_ \ underline_ \ end = begin 0 \ 0 \ 0 \ underline_ \ underline_ \ underline_ \ underline_ \ end $$

Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:

В результате получим вектор-столбец $ underline<bold> $ токов из семи элементов, состоящий из искомых токов, записанный в общем виде. Видим, что программный комплекс Matlab позволяет существенно упростить решение сложных систем уравнений, составленных по законам Кирхгофа.

Список использованной литературы

1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.

Рекомендуемые записи

При расчёте электрических цепей, помимо законов Кирхгофа, часто применяют метод контурных токов. Метод контурных токов…

Расчёт матриц передачи многополюсников различной формы осуществляется достаточно просто. Матрицы передачи — это математическое описание рассматриваемой…

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:Лекция 117. Правила КирхгофаСкачать

Правила (законы) Кирхгофа простыми словами

На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.

Учёный Густав Киргхоф сформулировал два правила [1], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.

Видео:Применение законов Кирхгофа при решении задачСкачать

Первое правило Кирхгофа

Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.

Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.

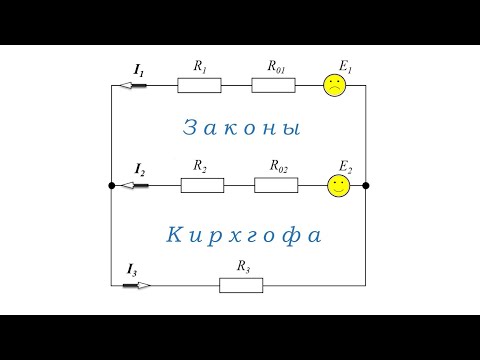
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.

Рис. 1. Схема контура

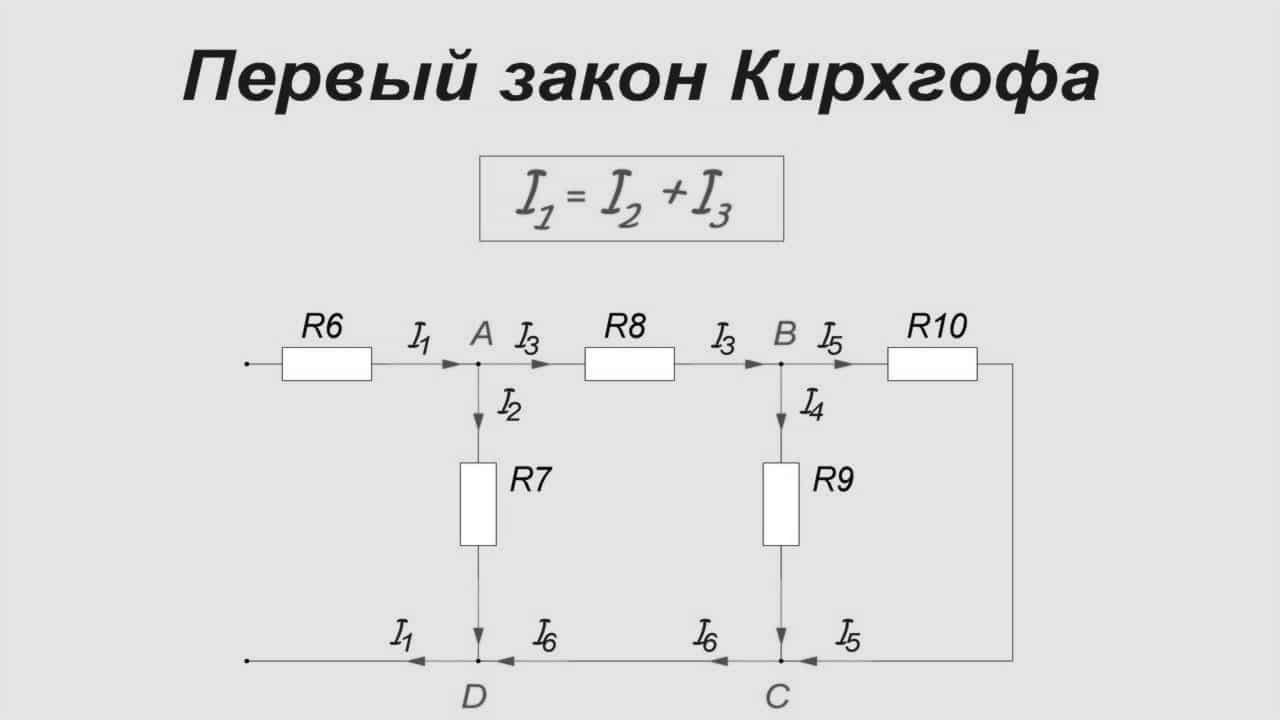
Ток I₁ входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I₁ = I₂ + I₃.

На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i₁, i₂, i₃, i₄ то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i₁ + i₂ + i₃ + i₄ = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.

Запишем наши выводы в алгебраической форме, для общего случая:

Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.

Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.

Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».

Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.

Видео:Как составить уравнения по законам Кирхгофа?Скачать

Второе правило Киргхофа

Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.

Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.

При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.

Рис. 4. Иллюстрация второго правила Кирхгофа

Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.

Формулировки уравнений общего характера:

, где где L_k и C_k – это индуктивности и ёмкости, соответственно.

Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.

Видео:Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать

Закон Кирхгофа для магнитной цепи

Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.

То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.

Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).

Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.

Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.

При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».

Видео:Урок 265. Задачи на правила КирхгофаСкачать

Примеры расчета цепей

Рассмотрим ещё раз рисунок 3. На нём изображено 4 разнонаправленных вектора: i₁, i₂, i₃, i₄. Из них – два входящие ( i₂, i₃) и два исходящие из узла (i₁, i₄). Положительными будем считать те векторы, которые направлены в точку соединения ветвей, а остальные – отрицательными.

Тогда, по формуле Кирхгофа, составим уравнение и запишем его в следующем виде: – i₁ + i₂ + i₃ – i₄ = 0.

На практике такие узлы являются частью контуров, обходя которые можно составить ещё несколько линейных уравнений с этими же неизвестными. Количество уравнений всегда достаточно для решения задачи.

Рассмотрим алгоритм решения на примере рис. 5.

Рис. 5. Пример для расчёта

Схема содержит 3 ветви и два узла, которые образуют три пары по два независимых контура:

Запишем независимое уравнение, выполняющееся, например, в точке а. Из первого правила Кирхгофа вытекает: I₁ + I₂ – I₃ = 0.

Воспользуемся вторым правилом Кирхгофа. Для составления уравнений можно выбрать любой из контуров, но нам необходимы контуры с узлом а, так как для него мы уже составили уравнение. Это будут контуры 1 и 2.

Пишем уравнения:

Решаем систему уравнений:

Так как значения R и E известны (см. рисунок 5), мы придём к системе уравнений:

Решая эту систему, получим:

Потенциал узла а равен: U_a = I₃*R₃ = 3,55 × 3 = 10,65 В. Чтобы убедиться в верности наших расчётов, проверим выполнение второго правила по отношению к контуру 3:

E₁ – E₂ + I₁R₁+ I₂R₂ = 12 – 15 + 1,36 – 4,38 = – 0,02 ≈ 0 (с учётом погрешностей, связанных с округлениями чисел при вычислениях).

Если проверка выполнения второго правила успешно завершена, то расчёты сделаны правильно, а полученные данные являются достоверными.

Применяя правила (законы) Кирхгофа можно вычислять параметры электрической энергии для магнитных цепей.

🎦 Видео

Урок 14. Законы Кирхгофа простыми словами с примерамиСкачать

Законы Кирхгофа. Метод контурных уравненийСкачать

Цепи переменного тока. Найти токи в цепи по законам КирхгофаСкачать

☠#8 Урок. Законы Кирхгофа - САМОЕ ПРОСТОЕ ОБЪЯСНЕНИЕ!Скачать

Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Расчет параметров электрической цепи методом непосредственного применения законов КирхгофаСкачать

Первый закон Кирхгофа! Хочешь понять? Посмотри!Скачать

Лекция 020-1. Цепи постоянного тока. Расчет при помощи уравнений КирхгофаСкачать

Второй закон Кирхгофа. Смотри и изучай!Скачать

Законы Кирхгофа, теория и практическое применениеСкачать