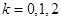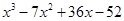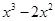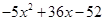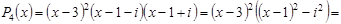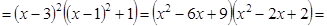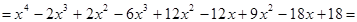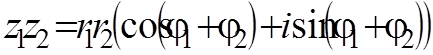Сколько решений в комплексных числах имеет уравнение

Квадратный корень из комплексного числа

Корни четвертой и пятой степени

Возведение в степень

Мнимая и действительная часть

Можно использовать следующие функции от z (например, от z = 1 + 2.5j):

Правила ввода выражений и функций

3.14159.. e Число e — основание натурального логарифма, примерно равно

2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности

© Контрольная работа РУ — калькуляторы онлайн

Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Где учитесь?

Для правильного составления решения, укажите:

Видео:Сколько решений имеет уравнение ?Скачать

Решение уравнений с комплексными числами

Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.

Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:

где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = .

Пример 1. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа

Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.

Пример 2. Найти все корни уравнения

Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:

Найдем корни уравнения:

Ответ:

Пример 3. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа

Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = . Найдем модуль комплексного числа:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:

Пример 4. Найти корни уравнения

Решение кубического уравнения комплексными числами:

Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.

Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:

Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.

Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.

После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.

Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.

Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.

Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.

Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.

Видео:Комплексные числа в уравненияхСкачать

Примеры решения алгебраических уравнений на множестве комплексных чисел (Приведите примеры решения алгебраических уравнений на множестве комплексных чисел)

1. Алгебраические уравнения первой степени:

, – единственный простой корень.

.

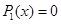
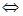
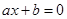
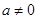
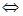
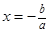
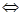
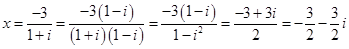
Ответ: .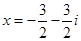

2. Квадратные уравнения:

, – всегда имеет два корня (различных или равных).

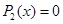
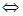
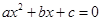
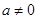
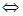
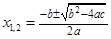
1) .

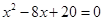
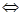
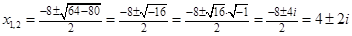
Ответ: .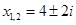

2) .

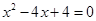
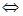
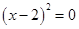
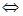
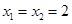
Ответ: .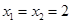

3) , .

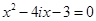
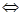
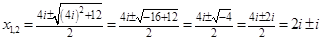
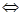
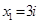
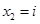
Ответ: , .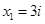

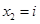
3. Двучленные уравнения степени :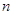

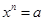
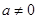
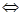
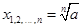
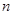
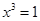
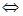
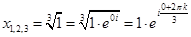
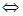
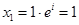
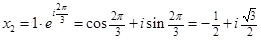
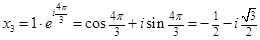
, – всегда имеет различных корней.

,

;

;

.

Ответ: , .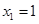

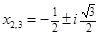
4. Решить кубическое уравнение .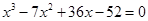

Уравнение третьей степени 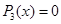имеет три корня (действительные или комплексные), при этом нужно считать каждый корень столько раз, какова его кратность. Так как все коэффициенты данного уравнения являются действительными числами, то комплексные корни уравнения, если они есть, будут парными комплексно сопряженными.

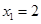
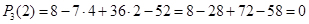
Подбором находим первый корень уравнения , так как .

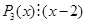
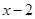
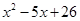
По следствию из теоремы Безу . Вычисляем это деление «в столбик»:

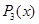
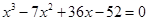
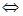
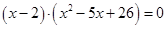
Представляя теперь многочлен в виде произведения линейно и квадратного множителя, получим:

.

Другие корни находим как корни квадратного уравнения:

.

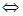
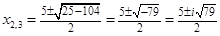
Ответ: , .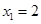

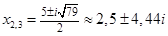
5. Составить алгебраическое уравнение наименьшей степени с действительными коэффициентами, если известно, что числа x1 = 3 и x2 = 1 + i являются его корнями, причем x1 является двукратным корнем, а x2 — простым.

Число 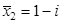тоже является корнем уравнения, т.к. коэффициенты уравнения должны быть действительными.

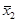
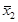
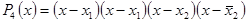
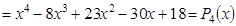
Всего искомое уравнение имеет 4 корня: x1, x1, x2, . Поэтому его степень равна 4. Составляем многочлен 4-й степени с нулями x1, x1, x2, по формуле (6):

Þ

.

Искомое уравнение имеет вид P4(x) = 0.

Ответ: .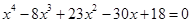

Вопросы для самопроверки

1. Сформулируйте определение комплексного числа

2. Что называется комплексным числом?

3. Какое название или смысл имеет формула?

4. Поясните смысл обозначений в этой формуле:

5. ⌂ .

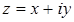
6. Что такое мнимая единица?

7. Что такое действительная часть комплексного числа z?

8. Что такое мнимая часть комплексного числа z?

9. Что такое комплексно сопряженное число?

10. Что такое противоположное число?

11. Что такое комплексный ноль?

12. Что такое чисто мнимое число?

13. Сформулируйте смысл комплексного равенства.

14. В чём состоит геометрическое изображение комплексных чисел?

15. Что такое модуль и аргумент комплексного числа?

16. Что называется модулем комплексного числа?

17. Что такое аргумент комплексного числа?

18. Какое название или смысл имеет формула?

19. Поясните смысл обозначений в этой формуле:

20. ⌂ .

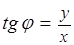
21. Что такое алгебраическая и тригонометрическая формы комплексного числа?

22. Какое название или смысл имеет формула?

23. Поясните смысл обозначений в этой формуле:

24. ⌂ .

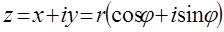
25. Что называется алгебраической формой комплексного числа?

26. Что называется тригонометрической формой комплексного числа?

27. Дайте определения и перечислите основные свойства арифметических действий над комплексными числами.

28. Какое название или смысл имеет формула?

29. Поясните смысл обозначений в этой формуле:

31. Какое название или смысл имеет формула?

32. Поясните смысл обозначений в этой формуле:

33. ⌂ .

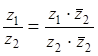
34. Какое название или смысл имеет формула?

35. Поясните смысл обозначений в этой формуле:

36. ⌂ .

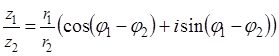
37. Что такое формула Муавра?

38. Какое название или смысл имеет формула?

39. Поясните смысл обозначений в этой формуле:

40. ⌂ .

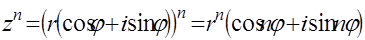
41. Что называется корнем степени n из комплексного числа?

42. Какое название или смысл имеет формула?

43. Поясните смысл обозначений в этой формуле:

44. ⌂ .

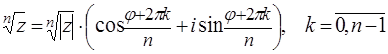
45. Что называется показательной формой комплексного числа?

46. Какое название или смысл имеет формула?

47. Поясните смысл обозначений в этой формуле:

48. ⌂ .

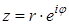
49. Что такое формулы Эйлера?

50. Какое название или смысл имеет формула?

51. Поясните смысл обозначений в этой формуле:

52. ⌂ .

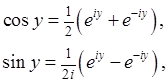
53. Что называется целой функцией?

54. Что называется алгебраическим многочленом?

55. Что называется полиномом?

56. Что такое степень многочлена?

57. Что такое коэффициенты многочлена?

58. Что называется алгебраическим уравнением n-й степени?

59. Что называется нулем функции?

60. Что называется корнем уравнения?

61. Перечислите основные свойства многочленов.

62. Сформулируйте свойство о тождественном равенстве многочленов.

63. Сформулируйте свойство о делении многочлена на разность (x – х0).

64. Сформулируйте теорему теорема Безу.

65. Какое название или смысл имеет формула?

66. Поясните смысл обозначений в этой формуле:

67. ⌂ .

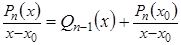
68. Сформулируйте свойство о существовании нуля многочлена.

69. Сформулируйте теорему теорема алгебры основная.

70. Какое название или смысл имеет формула?

71. Поясните смысл обозначений в этой формуле:

72. ⌂ .

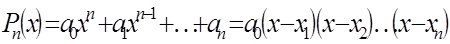
73. Что называется k-кратным нулем многочлена?

74. Что называется простым нулем многочлена?

75. Сформулируйте свойство о количестве корней алгебраического уравнения.

76. Сформулируйте свойство о комплексных корнях алгебраического уравнения

77. с действительными коэффициентами.

78. Сформулируйте свойство о разложении многочлена с действительными коэффициентами на линейные и квадратичные множители.

79. Приведите примеры решения алгебраических уравнений на множестве комплексных чисел

k-кратным нулем многочлена называется. (стр. 18)

алгебраическим многочленом называется. (стр. 14)

алгебраическим уравнением n-й степени называется. (стр. 14)

алгебраической формой комплексного числа называется. (стр. 5)

аргумент комплексного числа это. (стр. 4)

действительная часть комплексного числа z это. (стр. 2)

комплексно сопряженное число это. (стр. 2)

комплексный ноль это. (стр. 2)

комплексным числом называется. (стр. 2)

корнем степени n из комплексного числа называется. (стр. 10)

корнем уравнения называется. (стр. 14)

коэффициенты многочлена это. (стр. 14)

мнимая единица это. (стр. 2)

мнимая часть комплексного числа z это. (стр. 2)

модулем комплексного числа называется. (стр. 4)

нулем функции называется. (стр. 14)

показательной формой комплексного числа называется. (стр. 11)

полиномом называется. (стр. 14)

простым нулем многочлена называется. (стр. 18)

противоположное число это. (стр. 2)

степень многочлена это. (стр. 14)

тригонометрической формой комплексного числа называется. (стр. 5)

🔥 Видео

Комплексные корни квадратного уравненияСкачать

Алгебраическое определение количества решений системы линейных уравнений | Алгебра IСкачать

Комплексные числа и "золотое" уравнениеСкачать

Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Комплексные числа: начало. Высшая математика или школа?Скачать

Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

✓ Сколько же решений? | Опять кто-то неправ #019 | Борис Трушин, Valery Volkov & MindYourDecisionsСкачать

комплЕксные ЧИСЛА решение примеров МАТЕМАТИКАСкачать

Высшая математика. Комплексные числаСкачать

✓ Задача про комплексное число | Ботай со мной #101 | Борис ТрушинСкачать

Решение квадратных уравнений в поле комплексных чиселСкачать

Изобразить область на комплексной плоскостиСкачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Математика это не ИсламСкачать

Как мнимые числа спасли математику [Veritasium]Скачать

Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать