 Рациональные корни многочленов с целыми коэффициентами Рациональные корни многочленов с целыми коэффициентами |
 Алгебраические и трансцендентные числа Алгебраические и трансцендентные числа |
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Рациональные корни многочленов с целыми коэффициентами
Прежде, чем дать общую формулировку теоремы о рациональных корнях многочленов с целыми коэффициентами , решим следующую задачу.
Задача . Найти все корни уравнения
Решение . Предположим, что рассматриваемое уравнение имеет корень, являющийся рациональным числом. Тогда, поскольку каждое рациональное число можно представить в виде несократимой дроби

где m – число целое, а n – число натуральное, то выполняется равенство:
Умножая это равенство на n 3 , получаем равенство:
| 2m 3 + m 2 n – 5 m n 2 – – 3n 3 = 0. | (1) |
Теперь преобразуем равенство (1):
Отсюда вытекает, что число 2m 3 нацело делится на число n . А из этого, в свою очередь, следует, что, поскольку числа m и n не имеют общих простых делителей, то число n является делителем числа 2 . Таким образом, число n равно 1 или 2 .
Теперь преобразуем равенство (1) по-другому:
Значит, число 3n 3 нацело делится на число m . А из этого, в свою очередь, следует, что, так как числа m и n не имеют общих простых делителей, то число m является делителем числа 3. Таким образом, число m может быть равно: – 1, 1, – 3 или 3 .
Далее, рассматривая все возможные комбинации чисел m и n , получаем, что дробь
может принимать только следующие значения:
Таким образом, если у исходного уравнения и есть рациональный корень, то искать его нужно среди полученных шести чисел. Других рациональных корней у исходного уравнения быть не может.
Подставляя поочередно каждое из этих чисел в исходное уравнение, получаем, что корнем уравнения является лишь число 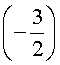
Оставляя читателю проверку того, что другие числа корнями исходного уравнения не являются, покажем, что число 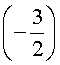
Ответ . Число 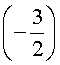
Замечание . Для того, чтобы найти все остальные корни исходного уравнения, нужно, воспользовавшись теоремой Безу, разделить многочлен
В результате деления получится квадратный трехчлен
Теорема . Если рациональное число (несократимая дробь)

где m – число целое, а n – число натуральное, является корнем многочлена k -ой степени
которого являются целыми числами, то числитель дроби m является делителем коэффициента ak , а знаменатель дроби n является делителем коэффициента a0 .
Коэффициент a0 называют старшим коэффициентом многочлена, а коэффициент ak – свободным членом многочлена.
Видео:Сколько корней имеет уравнение?Скачать

Алгебраические и трансцендентные числа
Определение . Действительное число называют действительным алгебраическим числом , если существует многочлен с целочисленными коэффициентами, корнем которого это число является. Если же такой многочлен не существует, то указанное число называют действительным трансцендентным числом .
Замечание . Числа π и e – наиболее известные примеры действительных трансцендентных чисел.
Утверждение . Каждое рациональное число является алгебраическим числом.
Доказательство . Каждое рациональное число представимо в виде несократимой дроби

где m – число целое, а n – число натуральное. Но указанная дробь является корнем уравнения первой степени
что и требовалось доказать.
Следствие . Каждое действительное трансцендентное число является иррациональным числом.
Видео:Рациональные корни многочлена с целым показателем. 10 класс.Скачать

10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ
Умножим обе части равенства (1) на (q ≠ 0). Получаем
В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому
Но когда мы записываем рациональное число в виде p/q, то эта дробь считается несократимой, то есть р и q не имеют общих делителей. Произведение a0q n может делиться на р (если р и q — взаимно простые числа) только тогда, когда a0 делится на р. Таким образом, р — делитель свободного члена a0.
Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда
Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a0. Таким образом, имеет место:
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене f (х) коэффициент аn = 1, то делителями аn могут быть только числа ±1, то есть q =±1, и имеет место:
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Задача 1 Найдите рациональные корни многочлена 2х 3 – х 2 + 12х – 6.
Пусть несократимая дробь p/q является корнем многочлена. Тогда р необходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.
Таким образом, рациональные корни многочлена необходимо искать среди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.
Кроме того, по схеме Горнера можно записать, что
Многочлен 2х 2 + 12 не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень x =1/2.
Задача 2 Разложите многочлен Р (х) = 2х 4 + 3х 3 – 2х 2 – х – 2 на множители.
Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.
Тогда Р (х) = (х – 1)(2х3 + 5х 2 + 3х + 2). Ищем целые корни кубического многочлена 2х 3 + 5х 2 + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на х + 2
Квадратный трехчлен 2х 2 + х +1 не имеет действительных корней и на линейные множители не раскладывается.
Ответ: Р (х) = (х – 1)(х + 2)(2х 2 + х +1).
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х 2 + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры доказывается, что многочлен нечетной степени всегда можно разложить на линейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.
Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Задача 3 Разложите на множители многочлен х 4 + х 3 + 3х 2 + х + 6.
Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
где а, b, с и d — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
 |
| Математика: полный курс решений задач в виде лекций |
Другие темы которые вам помогут понять математику:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
🔍 Видео
Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Сколько корней имеет уравнение?Скачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

✓ Теорема Безу. Рациональные нули многочленов | Ботай со мной #119 | Борис ТрушинСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ. §7 алгебра 8 классСкачать

Как решать уравнения с дробью? #shortsСкачать

Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

8 класс, 28 урок, Рациональные уравнения как математические модели реальных ситуацийСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Квадратный корень. 8 класс.Скачать

Как считать корни? #shortsСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать


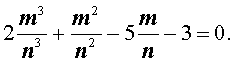
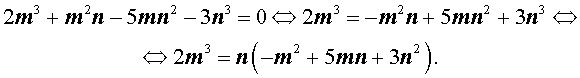
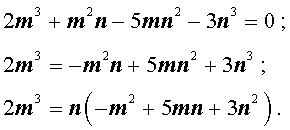
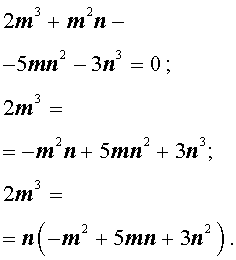
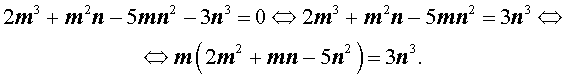
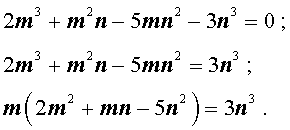
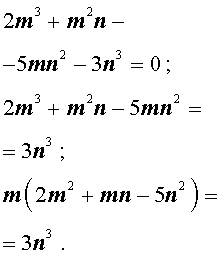
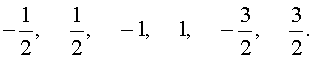
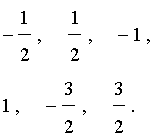
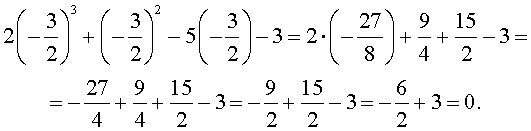
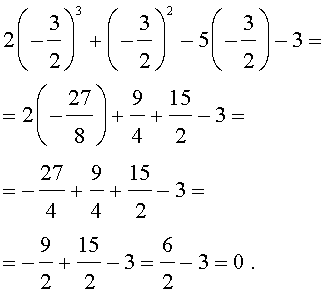
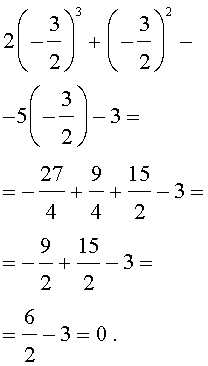
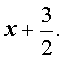







 с целыми коэффициентами существует рациональный корень, то этот корень имеет вид
с целыми коэффициентами существует рациональный корень, то этот корень имеет вид
 является корнем многочлена
является корнем многочлена  с целыми коэффициентами:
с целыми коэффициентами:
 :
:
 , содержит множитель
, содержит множитель  и каждый член, кроме члена
и каждый член, кроме члена  , содержит множитель
, содержит множитель  , то коэффициент
, то коэффициент  должен делится на
должен делится на  , а коэффициент
, а коэффициент  должен делится на
должен делится на  .
. .
. ,
,  запишем все возможные числа вида
запишем все возможные числа вида
 , т.е. одним из множителей является двучлен
, т.е. одним из множителей является двучлен  . Другие множители найдем, используя синтетическое деление:
. Другие множители найдем, используя синтетическое деление:


 , получим, что
, получим, что  являются корнями многочлена.
являются корнями многочлена. .
.
 , то, решив квадратное уравнение
, то, решив квадратное уравнение  , получим другие корни:
, получим другие корни:  . Значит данный многочлен третьей степени имеет три корня: —
. Значит данный многочлен третьей степени имеет три корня: — .
. сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми.
сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми. надо умножить все члены уравнения
надо умножить все члены уравнения  на 12, а затем решить полученное уравнение
на 12, а затем решить полученное уравнение  .
. (обращающее значение многочлена в нуль), которое является корнем многочлена, т.е. определяется двучлен
(обращающее значение многочлена в нуль), которое является корнем многочлена, т.е. определяется двучлен  , на который многочлен делится без остатка.
, на который многочлен делится без остатка. определяется другой множитель.
определяется другой множитель. могут являться числа ±1.
могут являться числа ±1. ;
;  . Значит, многочленах
. Значит, многочленах  не имеет рациональных корней.
не имеет рациональных корней. имеет один корень:
имеет один корень: 
 имеет два корня:
имеет два корня:  ,
,  ;
; 
 имеет три корня:
имеет три корня: 
 имеет четыре корня:
имеет четыре корня: 
 имеет кратные корни, получим 5 корней:
имеет кратные корни, получим 5 корней: 
 .
. .
. .
. является корнем данного многочлена
является корнем данного многочлена  . Другие корни найдем синтетическим делением.
. Другие корни найдем синтетическим делением.
 для множителя
для множителя  вновь применим теорему о рациональных корнях и синтетическое деление. Тогда
вновь применим теорему о рациональных корнях и синтетическое деление. Тогда 
 ;
;  . Решим уравнение
. Решим уравнение  ;
;  ;
;  (корень кратности 2);
(корень кратности 2);  ;
; 


