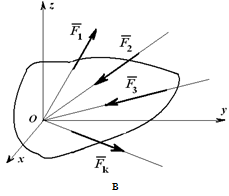
Выше (6.5, случай 6) было установлено, что
| Геометрической формой условия равновесия произвольной пространственной системы сил является равенство нулю ее главного вектора и главного момента |
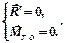
Учитывая, что 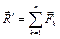



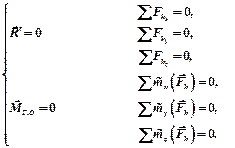
Последние три уравнения имеют место из-за того, что проекция момента силы относительно точки на ось, которая проходит через эту точку, равна моменту силы относительно оси (формула (6.9)).
| Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил системы на три координатные оси и суммы моментов всех сил системы относительно этих координатных осей равнялись нулю. |
Вывод. При решении задач на равновесие произвольной пространственной системы сил, которая приложена к твердому телу, мы должны составить шесть уравнений равновесия (6.19), потому имеем возможность с помощью этих уравнений определить шесть неизвестных величин.
Рассмотрим случай пространственной системы параллельных сил. Систему координат выберем так, чтобы ось Оz была параллельна линиям действия сил (рис. 6.11).
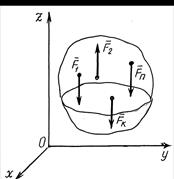 Рисунок 6.11 Рисунок 6.11 | Если система сил находится в равновесии, то имеют место уравнения (6.19). Система сил, показана на рис. 6.11, является упрощенным вариантом произвольной пространственной системы сил, потому и уравнения (6.19) должны упроститься. Выясним, какие из уравнений (6.19) в данном случае выполняются тождественно, то есть является лишними. Такими является: – суммы проекций сил на оси Оx и Оy, потому что силы 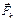 им перпендикулярны; – сумма моментов сил относительно оси Оz, потому что силы им перпендикулярны; – сумма моментов сил относительно оси Оz, потому что силы 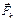 параллельны ей (п. 6.3. Рекомендации для практического занятия). параллельны ей (п. 6.3. Рекомендации для практического занятия). |
Таким образом, остались три уравнения:
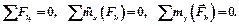
| Для равновесия параллельной пространственной системы сил необходимо и достаточно, чтобы: – сумма проекций сил системы на ось параллельную силам равнялась нулю; – суммы моментов сил системы относительно двух других осей равнялись нулю. |
Вывод. При решении задач на равновесие параллельной пространственной системы сил, которая приложена к твердому телу, мы должны составить три уравнения равновесия и имеем возможность с помощью этих уравнений определить три неизвестных величины.
На первой лекции по разделу «Статика» мы выяснили, что имеют место шесть разновидностей систем сил, которые могут встретиться в Вашей практике инженерных расчетов. Кроме того есть две возможности расположения пар сил : в пространстве и в плоскости. Сведем все уравнения равновесия для сил и для пар сил в одну таблицу (табл. 6.2), в которой в последней колонке отметим количество неизвестных величин, которые позволит определить система уравнений равновесия.
Таблица 6.2 – Уравнения равновесия разных систем сил
| Вид системы сил | Уравнения равновесия | Количество определяемых неизвестных |
Сходящаяся плоская 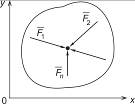 |  | |
Параллельная плоская (  оси 0у) оси 0у)  | 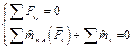 т. А – произвольная, принадлежащая плоскости 0ху т. А – произвольная, принадлежащая плоскости 0ху | |
Произвольная плоская (в плоскости 0ху)  | 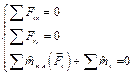 т. А – произвольная, принадлежащая плоскости 0ху т. А – произвольная, принадлежащая плоскости 0ху |
Продолжение таблицы 6.2
Система пар в плоскости 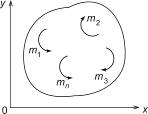 | 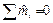 |
Сходящаяся пространственная 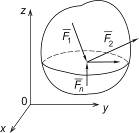 | 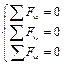 |
Параллельная пространственная ( 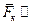 оси 0z) оси 0z) 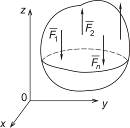 | 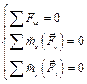 |
Продолжение таблицы 6.2
Произвольная пространственная 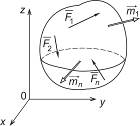 | 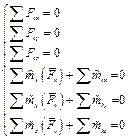 |
Система пар в пространстве 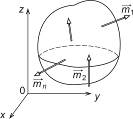 | 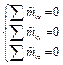 |
Вопросы для самоконтроля по теме 6
1. Как найти момент силы относительно оси?
2. Какая зависимость существует между моментом силы относительно точки и моментом этой же силы относительно оси, которая проходит через эту точку?
3. В каких случаях момент силы относительно оси равен нулю? А когда он наибольший?
4. В каких случаях система сил приводится к равнодействующей?
5. В каком случае пространственная система сил приводится:
– к динамическому винту?
6. Что называется инвариантом статики? Какие Вы знаете инварианты статики?
7. Запишите уравнения равновесия произвольной пространственной системы сил.
8. Сформулируйте необходимое и достаточное условие равновесия параллельной пространственной системы сил.
9. Изменится ли главный вектор системы сил при изменении центра приведения? А главный момент?
Тема 7. ФЕРМЫ. ОПРЕДЕЛЕНИЕ УСИЛИЙ
Видео:5.6. Равновесие произвольной пространственной системы силСкачать

Напряжение равноопасного состояния
ТЕСТ
Техническая механика
Заключительный этап Всероссийской олимпиады по укрупненной группе специальностей
АВИАЦИОННАЯ И РАКЕТНО-КОСМИЧЕСКАЯ ТЕХНИКА специальности 24.02.01 Производство летательных аппаратов, 24.02.02 Производство авиационных двигателей
Апреля 2016г.
На базе
ГБПОУ НСО «Новосибирский авиационный технический колледж»
Г. Новосибирск
1. Выбрать формулу для расчета главного вектора пространственной системе сил.
1)
2)
3)
4)
2. Сколько неизвестных величин можно найти, используя уравнения равновесия пространственной системы сходящихся сил?
3) 3
3.Какие уравнения равновесия нужно использовать, чтобы найти 
1)
2)
3)
4)
4. Определить сумму моментов сил относительно 


5. Найти X 







КН
6. Прямой брус нагружается внешней силой F. После снятия нагрузки его форма и размеры полностью восстанавливаются. Какие деформации имели место в данном случае?
Упругие
7. Как называется способность конструкции сопротивляться упругим деформациям?
Жесткость
8. По какому из уравнений, пользуясь методом сечения, можно определить продольную силу в сечении?
1)
2) Q
3) N=
4) M
9. Пользуясь методом сечения, определить величину поперечной силы в сечении I-I.
КН
10. Какие напряжения возникают в поперечном сечении I-I бруса под действием крутящего момента M 
Õ – нормальное напряжение
ȶ — касательные напряжения
1) ȶ
4)
11. В какой точке диаграммы растяжения на образце образуется шейка?
3) 3
12. До какого из приведенных напряжений в материале выполняется зависимость
1) до
2) до
3) до
4) до
13. Выбрать точную запись условия прочности при растяжении и сжатии.
1)
2)
3)
4)
14. Определить допускаемое напряжение до материала, если полученные следующие данные:
F 
F 
F 
Нормативный запас прочности 2,5;
Площадь поперечного сечения образца 200мм²
МПа
15. Проверить прочность материала, если: максимальное напряжение в сечении 



1)
2)
3)
4) Данных недостаточно
16. Как называется и обозначается напряжение, при котором деформации растут при постоянной нагрузке?
1) Предел прочности
2) Предел текучести
3) Допускаемое напряжение
4) Предел пропорциональности
17 Определить допускаемое напряжение, если:
F 
F 
F 
Запас прочности s=2
Площадь поперечного сечения А=40 мм²
МПа
18. Определить максимальное удлинение в момент разрыва, если:
начальная длина образца 200мм
а длина в момент разрыва 240 мм

1)
2)
3)
4 ) δ,
20. Проверить прочность материала, если: максимальное напряжение в сечении 



Запас прочности s=1,5
1)
2)
3)
4) Данных недостаточно
21. Листы соединены болтом, поставленным без зазора. Соединение нагружено растягивающей силой F=50,4 кН. Рассчитать величину площади среза болта, если d 
22. Выбрать формулу для расчета напряжения сдвига в поперечном сечении болта (рисунок к вопросу 21)
1)
2)
3)
4)
23. Рассчитать площадь смятия внутреннего листа соединения (рисунок к вопросу №1), если допускаемое напряжение смятия материала листа – 120 МПа. Остальные данные для расчета – в вопросе 21
24. Проверить прочность на смятие внутреннего листа соединения (рисунок к вопросу 21), если допускаемое напряжение смятия материала листа – 120 МПа. Остальные данные для расчета – в вопросе 21
1)
2)
3)
4) Для ответа данных недостаточно
25. Из расчета заклепок на срез определить допускаемую нагрузку на соединение. d=16мм, δ 


КН
26. Выбрать участок чистого изгиба
Й участок
27. Выберите формулу для расчета изгибающего момента в сечении 3-3
1)
2)
3)
4)
28. Определить величину изгибающегося момента в точке Г слева (схема к вопросу 27), если F 




29. Из представленных на схеме эпюр выбрать эпюру поперечной силы для изображенной балки
В
30. Из представленных в вопросе 29 эпюр выбрать эпюру изгибающих моментов для балки
Д
31. Определите реакцию в опоре В
КН
32. Определить поперечную силу в очке с координатой 2м.
КН
33. Определить изгибающий момент в точке С
34. Из представленных на схеме эпюр выбрать эпюру поперечной силы для балки
1) 1
35. Из представленных в вопросе 34 эпюр выбрать эпюру изгибающих моментов для балки
4) 6
36. Определить поперечную силу в любом сечении на 2 участке балки
КН
37. Вычислить величину изгибающего момента в сечении С
38. Для балки (вопрос 37) определить максимальное нормальное напряжение в сечении С. Сечение балки – швеллер №22
МПа
39. При каком поперечном сечении балка выдержит большую нагрузку?
Г
40. Нормальное напряжение при изгибе в точке В поперечного сечения балки 140 МПа. Определить нормальное напряжение в точке С
МПа
41. Определить поперечную силу в любом сечении на 2 участке балки
КН
42. Вычислить величину изгибающего момента в сечении D
43. Для балки (вопрос 37) определить максимальное нормальное напряжение в сечении D. Сечение балки – швеллер № 40
МПа
44. Выберите вариант поперечного сечения балки, при котором балка выдержит большую нагрузку

1) А
Б
45. Выбрать соответствующую эпюру распределения касательных напряжений по высоте сечения при поперечном изгибе
В
46. Какие напряжения возникают в точке поперечного сечения бруса при действии изгиба с кручением?
1)
2)
3)
4) Однозначного ответа нет
47. Какое напряжение называют «эквивалентным»?
1) Напряжение, равное действующему
Напряжение равноопасного состояния
3) Напряжение, равное геометрической сумме действующих напряжений
4) Напряжение равное алгебраической сумме действующих напряжений
48. Выбрать формулу для расчета эквивалентного расчета по теории максимальных касательных напряжений.
1)
2)
3)
4) Верный ответ не приведен
49. Выберите участок вала, где действует только изгибающий момент и поперечная сила.
Й участок
4)Такого участка нет
50. В опасном сечении стального бруса круглого поперечного сечения действует изгибающий момент 540 Н•м и крутящий момент 200 Н•м. Проверить прочность бруса, если его диаметр 60 мм, а допускаемое напряжение 160 МПа. Расчет произвести по гипотезе энергии формоизменения.
1)
2)
3)
Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

iSopromat.ru
Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:
Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.
Если система уравновешена, то получаем условия равновесия: R=0, MO=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:
Видео:Термех. Статика. Решение задач на равновесие пространственной системы телСкачать

Формы условий равновесия
Первая форма
Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:
причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.
Вторая форма
Уравнения равновесия могут быть записаны иначе:
Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.
Третья форма
Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.
Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.
Видео:5.5. Равновесие пространственной системы параллельных силСкачать

Другие условия равновесия
При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):
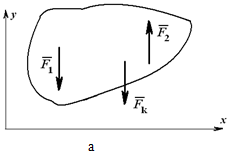
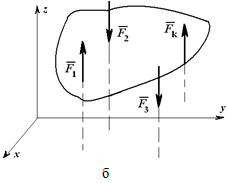
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:
Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:
и два уравнения для плоской системы:
В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Решение задач, контрольных и РГР
По желанию можете добавить файл или фото задания
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
🎬 Видео
Три формы уравнений равновесия произвольной плоской системы силСкачать

5.7. Равновесие системы тел под действием пространственной системы сил (1 из 2)Скачать

Равновесие системы телСкачать

2.6. Равновесие тела с учётом трения качения (1 из 2)Скачать

Теоретическая механика. Задание С5 (часть 9) из сборника ЯблонскогоСкачать

Решение задачи по теоретической механике, тема "Равновесие системы тел".Скачать

2.5. Равновесие тела с учётом трения скольженияСкачать

5.7. Равновесие системы тел под действием пространственной системы сил (2 из 2)Скачать

Произвольная плоская система сил. Задача 1Скачать

Определение опорных реакции в пространственной конструкции. ТермехСкачать

Статика. Варианты условий равновесия. Лекция (22)Скачать

Термех. Статика. Равновесие плоской произвольной системы силСкачать

2.6. Равновесие тела с учётом трения качения (2 из 2)Скачать

Статически неопределимые системыСкачать

2.3. Равновесие плоской системы параллельных сил (2 из 2)Скачать