Скачать презентацию уравнение прямой 9 класс мерзляк (6 видео)

Презентация по геометрии Мерзляк 9 класс. Угловой коэффициент в уравнении прямой

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Содержание

Описание презентации по отдельным слайдам:
Презентация урока по теме «Уравнение прямой» презентация к уроку по геометрии (9 класс) на тему
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Презентация к уроку геометрии по теме: «Уравнение прямой».
Просмотр содержимого документа «Презентация к уроку геометрии по теме: «Уравнение прямой».»
🌟 Видео

Описание презентации по отдельным слайдам:

Угловой коэффициент
в уравнении прямой

Какие из следующих утверждений верны?
I. 1. Площадь квадрата равна произведению двух его смежных сторон.
2. Диагональ трапеции делит её на два равных треугольника.
3. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
II. 1. Существует прямоугольник, который не является параллелограммом.
2. Треугольник с углами 40°, 70°, 70° — равнобедренный.
3. Если из точки M проведены две касательные к окружности и А и В — точки касания, то отрезки MA и MB равны.
III 1. Если в четырёхугольнике две стороны параллельны, то этот четырёхугольник — параллелограмм. 2. Через любые три точки плоскости, не лежащие на одной прямой, проходит единственная окружность.
IV. 1. Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2. Любой квадрат является ромбом.
3. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
V. 1. Если один из двух смежных углов острый, то другой тупой.
2. Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны..
3. Все хорды одной окружности равны между собой.

Какие из следующих утверждений верны?
VI. 1. Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники равны.
2. Сумма смежных углов равна 180°.
3. Любая медиана равнобедренного треугольника является его биссектрисой.
VII. 1. Вертикальные углы равны. 2. Две прямые, параллельные третьей прямой, перпендикулярны друг другу. 3. Диагонали любого прямоугольника делят его на 4 равных треугольника.
VIII. 1. Если радиус окружности равен 7, а расстояние от центра окружности до прямой равно 5, то эти прямая и окружность не имеют общих точек.
2. Сумма двух противоположных углов четырёхугольника равна 180. 3. Центр окружности, описанной около прямоугольного треугольника, лежит на стороне этого треугольника.
IX. 1. Диагонали любого прямоугольника равны.
2. Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
3 Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
X 1. Внешний угол треугольника равен сумме двух внутренних углов этого треугольника.
2. Центром вписанной в треугольник окружности является точка пересечения биссектрис этого треугольника.
3. Биссектрисы соседних углов параллелограмма взаимно перпендикулярны.

№ 1.
Найти расстояние между точками А и В,
если А(0;0), В(-5;12);

Видео:Уравнение прямой. Урок 6. Геометрия 9 классСкачать

Презентация урока по теме «Уравнение прямой»
презентация к уроку по геометрии (9 класс) на тему

ПЛАН-КОНСПЕКТ УРОКА «Уравнение прямой».

Тип урока урок изучения нового материала.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Скачать:

Вложение	Размер
uravnenie_pryamoy.pptx	548.4 КБ

Предварительный просмотр:

Видео:УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Подписи к слайдам:

Самостоятельная работа I вариант II вариант 1) Определите координаты центра и радиус окружности, заданной уравнением: а)(х+8) 2 +(у-5) 2 =16 а)(х-4) 2 + (у+2) 2 =4 б)х 2 +(у-10) 2 =25 б)(х+7) 2 + у 2 =9 2) Напишите уравнение окружности радиуса r с центром А, если: а) А(0; 5), r=3; а) А(-1; 2), r=2; б) А(-3; -7), r=6; б) А(4; -3), r=10 3) Напишите уравнение окружности с центром в начале координат, проходящей через заданную точку В(-4; 3) А(-6;8)

4 ) Составить уравнение окружности

Ответы 1 вариант 2 вариант 1 а) (- 8;5) r=4 б) (0;10) r=5 1 а) (4;-2) r=2 б) (-7;0) r= 3 2 а) х 2 +(у-5) 2 =9 б) (х+3) 2 +(у+7) 2 =36 2 а) (х+1) 2 +(у-2) 2 =4 б) (х-4) 2 +(у+3) 2 =100 3 х 2 +у 2 =25 3.х 2 +у 2 =100 4 (х-2) 2 +(у-2) 2 =4 4 (х-4) 2 +(у-3) 2 =25

Китайская пословица гласит: » Я слушаю, — я забываю ; Я вижу, — я запоминаю ; Я делаю, — я усваиваю.»

Практическое задание Начертите прямоугольную систему координат. Проведите произвольную прямую d . Отметьте точки А(х 1; у 1 ) и В(х 2 ;у 2 ) так, чтобы прямая d была серединным перпендикуляром к отрезку АВ. Отметьте на прямой d точку N ( х;у ) и постройте отрезки А N и В N . Получили А N = В N (почему?) или А N 2 = В N 2 . Напишите формулу расстояния между точками А и N , В и N .

Уравнение прямой ( х-х 1 ) 2 + (у-у 1 ) 2 =(х-х 2 ) 2 +(у-у 2 ) 2

после преобразований : 2х(х 1 -х 2 )+2у(у 1 -у 2 )+(х 2 2 +у 2 2 -х 1 2 -у 1 2 )=0 ах+ву+с=0 – уравнение прямой , где а=2х(х 1 -х 2 ), в=2у(у 1 -у 2 ), с = х 2 2 +у 2 2 -х 1 2 -у 1 2

1. Уравнение прямой В прямоугольной системе координат уравнение прямой имеет вид: ах+ву+с=0, где а,в,с — некоторые числа

2. Частные случаи расположения прямой: а ) а=0 , b ≠0, у = m

2.Частные случаи расположения прямой б) а ≠0 , b =0 , х= n

2. Частные случаи расположения прямой: в) а≠0, b ≠0 , с=0, у=кх

3. Уравнение прямой, не параллельной оси ординат Если а≠0, b≠0 , то уравнение ах+ b у+с=0 можно представить в виде у =кх+ m , где к=-а / b , m =-с / b

геометрический смысл коэффициента k Возьмем две точки на прямой А(х 1 ;у 1 ) и В(х 2 ;у 2 ), где х 1 Мне нравится

Видео:Уравнение прямой.Скачать

Презентация к уроку геометрии по теме: «Уравнение прямой».

Просмотр содержимого документа
«Презентация к уроку геометрии по теме: «Уравнение прямой».»

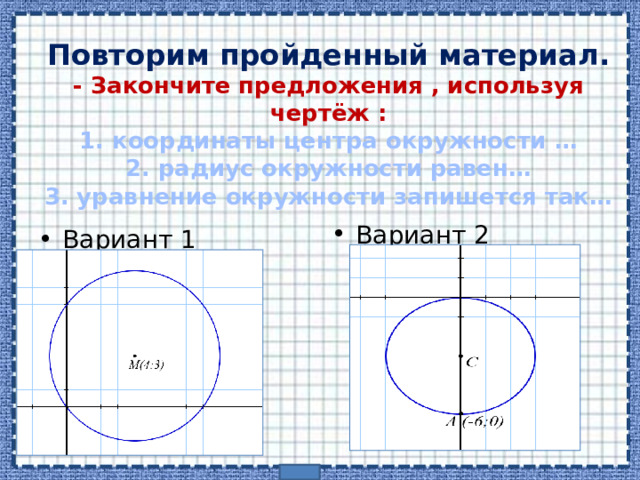
Повторим пройденный материал. — Закончите предложения , используя чертёж : 1. координаты центра окружности … 2. радиус окружности равен… 3. уравнение окружности запишется так…

Вариант 2

Вариант 1

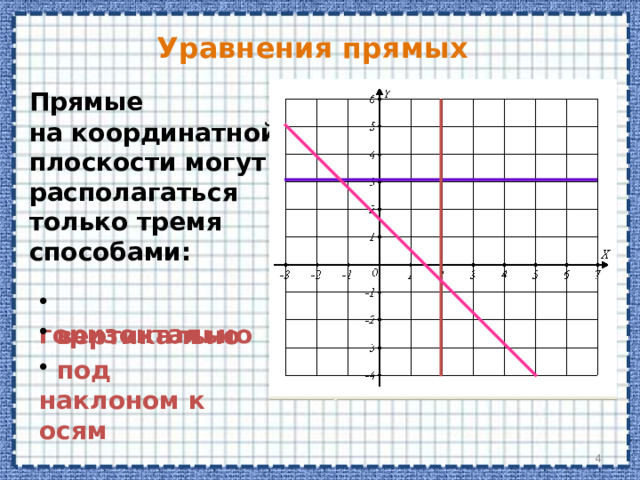
Прямые на координатной плоскости могут располагаться только тремя способами:

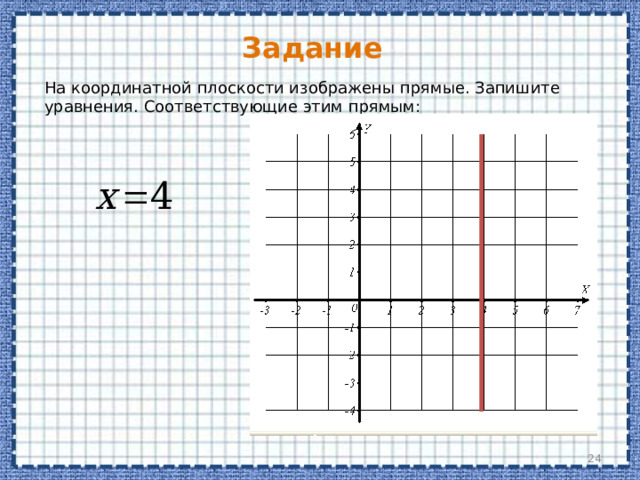
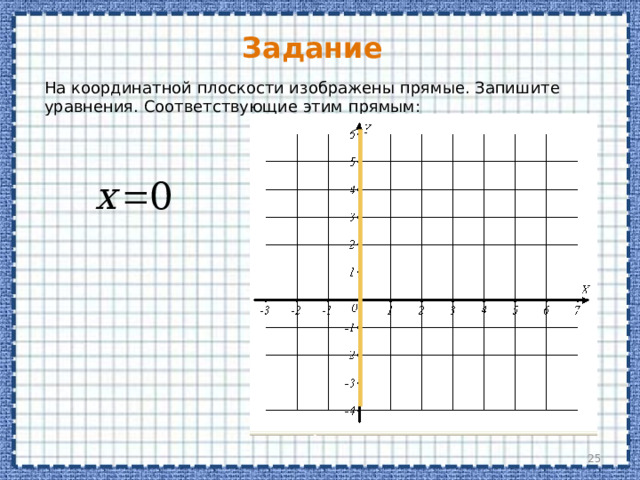
Уравнение вертикальных прямых

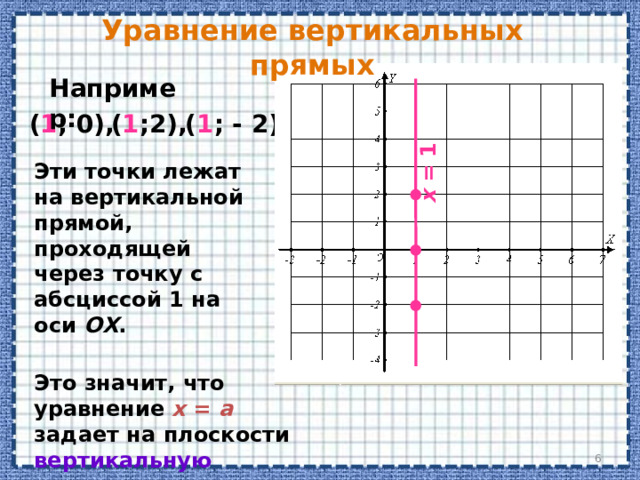
Уравнение вида x = a на координатной плоскости задает множество точек, имеющих одну и ту же абсциссу .

Рассмотрим, например, уравнение: x = 1

Отметим на координатной плоскости некоторые точки, имеющие абсциссу, равную 1.

Уравнение вертикальных прямых

Эти точки лежат на вертикальной прямой, проходящей через точку с абсциссой 1 на оси ОХ .

Это значит, что уравнение x = a задает на плоскости вертикальную прямую.

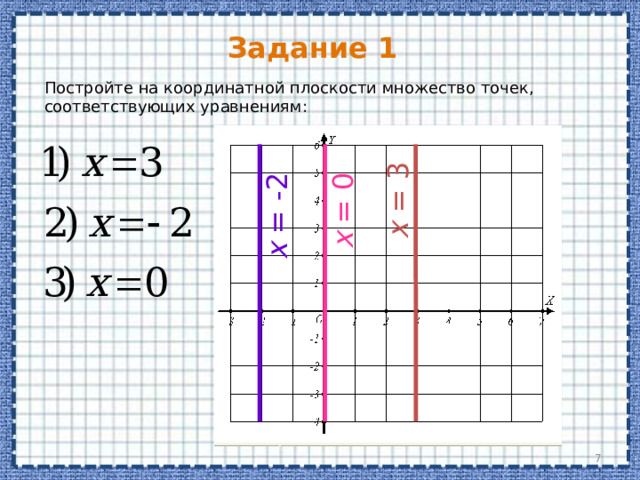
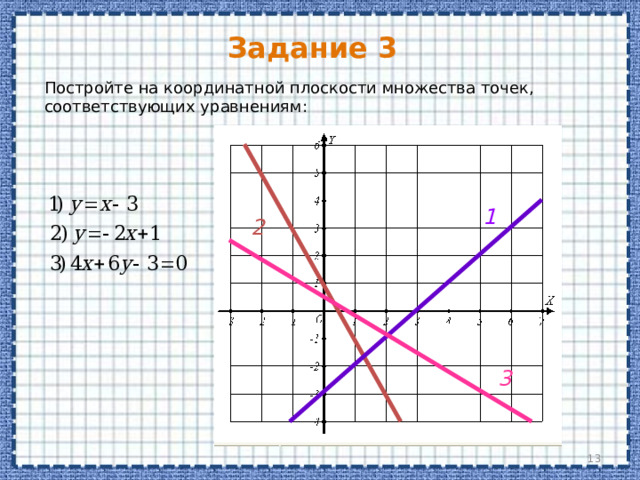
Постройте на координатной плоскости множество точек, соответствующих уравнениям:

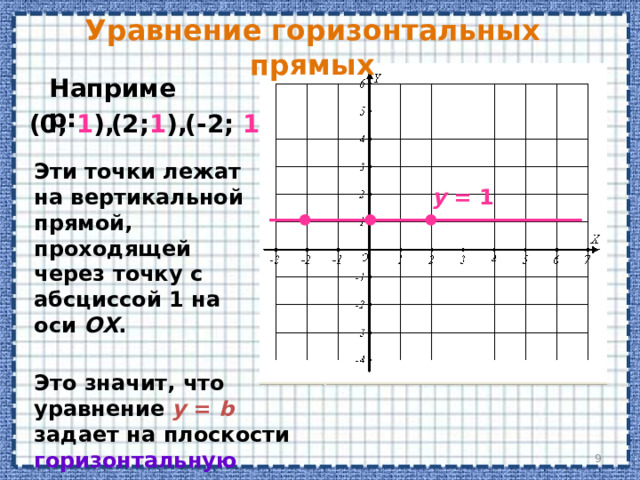
Уравнение горизонтальных прямых

Уравнение вида y = b на координатной плоскости задает множество точек, имеющих одну и ту же ординату.

Рассмотрим, например, уравнение: y = 1

Отметим на координатной плоскости некоторые точки, имеющие ординату, равную 1.

Уравнение горизонтальных прямых

Эти точки лежат на вертикальной прямой, проходящей через точку с абсциссой 1 на оси ОХ .

Это значит, что уравнение y = b задает на плоскости горизонтальную прямую.

Постройте на координатной плоскости множества точек, соответствующих уравнениям:

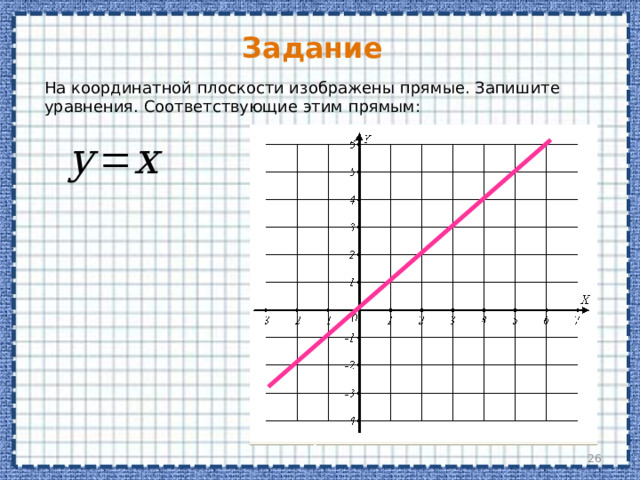
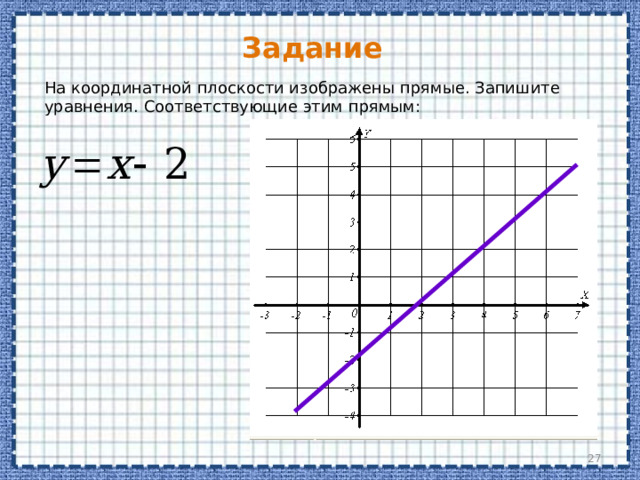
Каноническое уравнение прямых

Мы привыкли к тому, что на координатной плоскости прямая — это график линейной функции, которая задана уравнением вида:

Рассмотрим следующее уравнение прямой:

Каноническое уравнение прямых

В канонической записи уравнения прямых принято использовать целые коэффициенты.

Выполним обратную операцию :

Постройте на координатной плоскости множества точек, соответствующих уравнениям:

Условие параллельности прямых

Пусть заданы уравнения прямых :

Уравнение прямой, проходящей через две заданные точки

Запишем уравнение прямой, проходящей через точки А и В :

Если прямая проходит через точки А и В , то координаты этих точек можно подставить в уравнение прямой:

Получаем систему линейных уравнений с неизвестными k и b . Решив ее, находим значения k и b .

Уравнение прямой, проходящей через две заданные точки

Запишем уравнение прямой, проходящей через точки :

Подставим координаты в уравнение прямой:

Решаем систему линейных уравнений с неизвестными k и b .

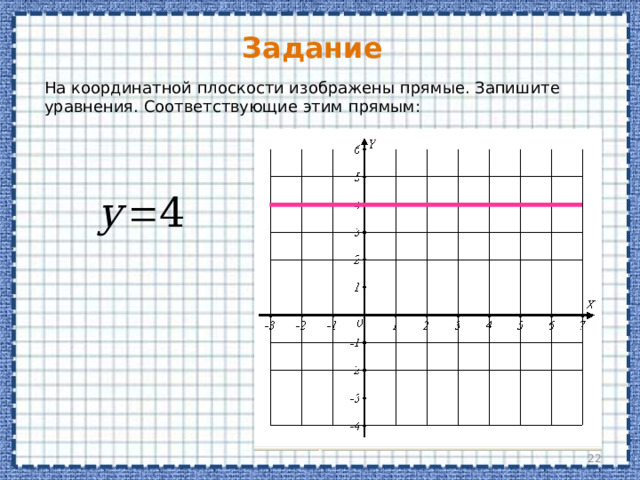
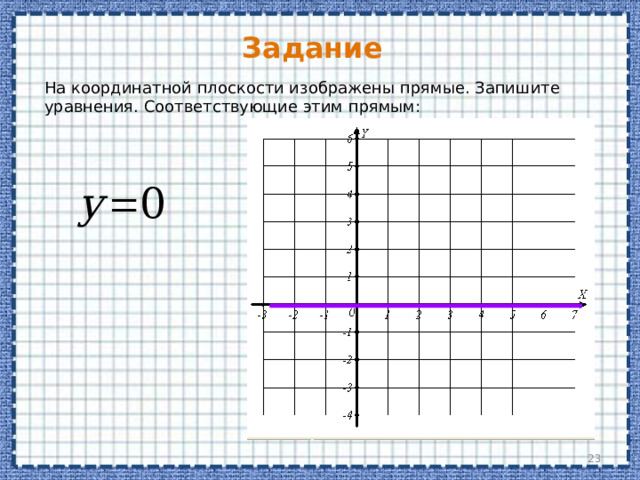
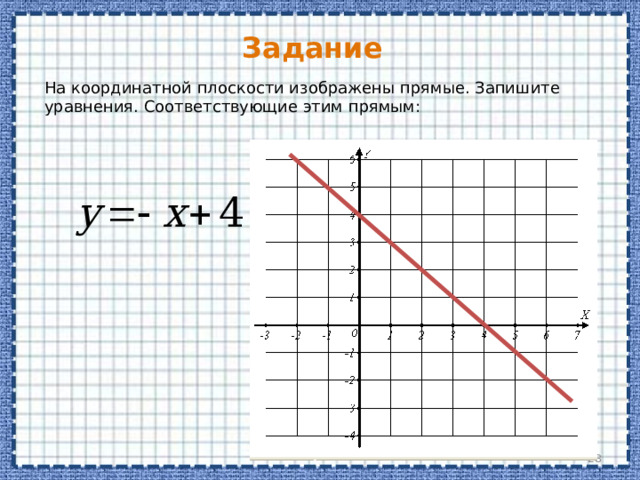
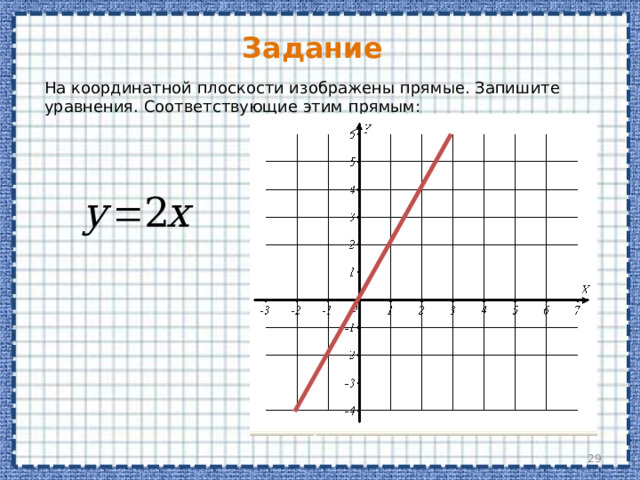
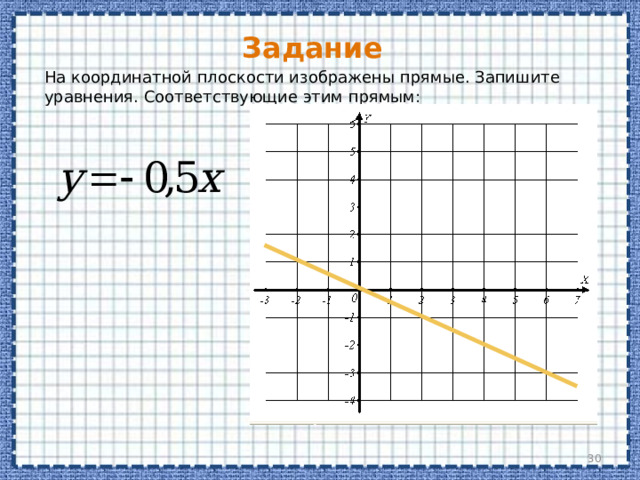
На координатной плоскости изображены прямые. Запишите уравнения. Соответствующие этим прямым:

Решение задач у доски.

Даны две точки А (1;-2) и В (2;4)а) Найдите координаты вектора ВА и разложите его по координатным векторам i и j.б) Найдите координаты середины отрезка АВ.в) Найдите длину отрезка АВ.г) Напишите уравнение окружности, имеющей центр в точке В и проходящей через точку Ад) Напишите уравнение прямой АВ

Напишите уравнение прямой АВ . КАК .

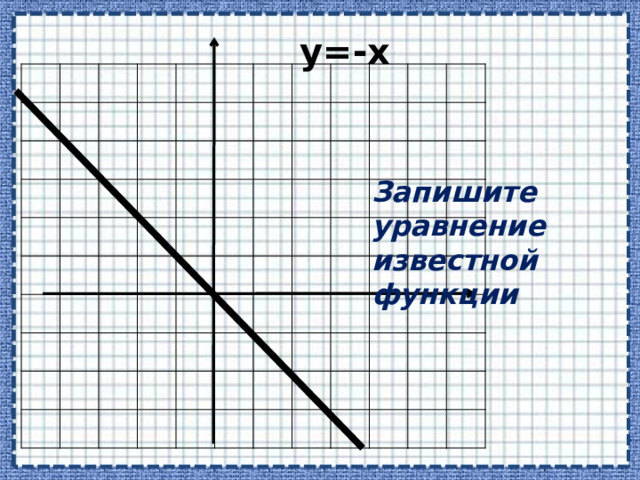
Запишите уравнение известной функции

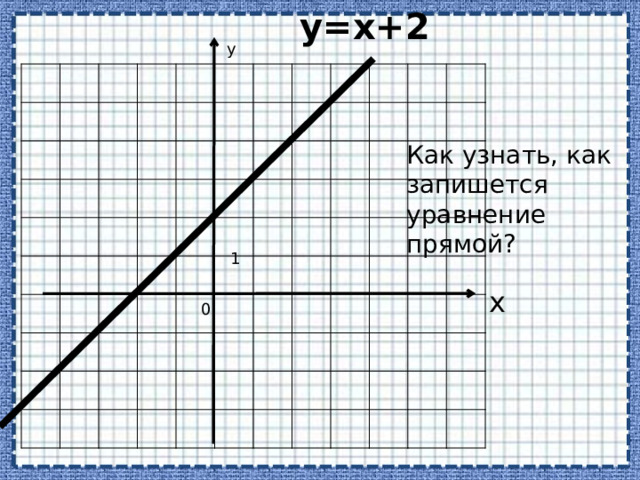
Как узнать, как запишется уравнение прямой?

Любая прямая в координатах x, y имеет уравнение вида: ax + by + c = 0, где a, b и c – некоторые числа, причем хотя бы одно из чисел a, b не равно нулю.

Пример.Составим уравнение прямой,которая проходит через точки А(-1; 1), B(1; 0).

Решение: Прямая имеет уравнение вида ax + by + c = 0. Подставляя координаты А и B в это уравнение, получим:
–a + b + c = 0,
a + c = 0.

Решим полученную систему:

Выразим коэффициенты a и b через коэффициент c :
В уравнении a + c = 0 : a = 0 – c = –c.
В уравнении –a + b + c = 0 находим значение b через c (одновременно заменив в нем и значение a уже найденным выше значением c): b = a – c = -c – c = -2c.
Итак, мы получили новые значенияaиb: a = -c, b = -2c.

Итак, мы получили новые значения a и b : a = -c, b = -2c. Теперь в уравнении прямой ax + by + c = 0 ставим полученные значения a и b : ax + by + c = — cx – 2cy + c = 0. Сокращаем c и получаем окончательное уравнение искомой прямой: -x – 2y + 1 = 0. или x + 2y — 1 = 0.