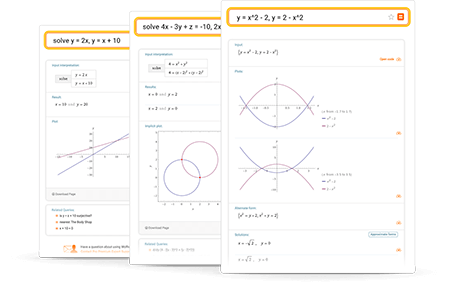
Достаточно войти на страницу wolframalpha набрать в текстовом поле свой запрос и нажать на кнопку «=»
(имеет всплывающую подсказку вычислить ) или просто нажать Enter .
Функционал Wolfram Alpha не ограничивается лишь поиском ответов на поставленные вопросы. С помощью этой системы можно, например, строить графики и сопоставлять различные данные, что намного наглядней и лучше воспринимается, чем просто текст. Кроме того, с помощью Wolfram Alpha можно производить математические операции, как элементарные (которые без проблем выполняет и Google), так и решать уравнения различной сложности. Также Wolfram Alpha умеет строить графики функций, вычислять значения синуса или косинуса и так далее.
Например можно решить вот такое уравнение :
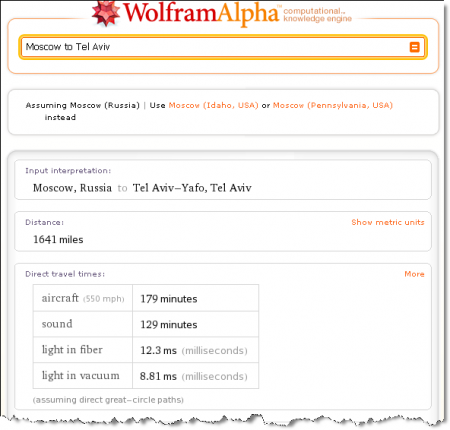
а чтобы узнать, какое расстояние между Москвой и Тель-Авивом, нужно ввести в поле
и вот вам результат:
Один из минусов сервиса Wolfram Alpha – это его англоязычность…так что если хотите задать вопрос системе придется писать его на английском языке. Даже неизвестно, появится ли русскоязычная версия этой поисково-вычислительной системы.
Основные команды для Вольфрам Альфа
(Команды вводятся в строку Вольфрама — например выше. Все команды заканчиваются нажатием Enter)
1. Решение уравнений, построение графиков
- Арифметические знаки плюс, минус, умножить, поделить +, — , *, / Примеры: 3*2, x*y, (a+b)/c
- Возведение в степень «x в степени а» x^a. Примеры x^a, x**a, (a+b)^2, (a+b)**2, (a+b)^(2x+1)
- Скобки. Действия в скобках ведутся первыми
- Функции .sin(x), cos(x), tan(x)=sin(x)/cos(x), cotan(x)=cos(x)/sin(x), sec(x)=1/cos(x), cosec(x)=1/sin(x)
- Функции log(x), exp(x), sinh(x), cosh(x), tanh(x), cotanh(x)
- Корень квадратный из «х» sqrt(x) или x^(1/2)
Чтобы вычислить выражение, нужно его просто ввести. Например корень из 2 будет выглядеть как sqrt(2) или же 2^(1/2).
2. Чтобы решить уравнение, нужно просто его ввести
3. Чтобы построить график, нужно использовать команду plot
Например нарисуем с помощью Вольфрама функцию 2^(-x) cos(x). Это делается командой plot (график).
Чтобы построить несколько графиков на одной координатной плоскости (например для визуализации решения систем уравнений), при значении переменной x в интервале (A,B), нужно использовать команду
4. Чтобы собрать множители из двучлена (многочлена) f, наберите factor[f]
5. Чтобы развалить произведение f на слагаемые, используйте команду expand[f]
6. Чтобы упростить выражение f[x], наберите команду Simplify[f[x]]
Например упростить «е в степени догарифм х»:
Simplify[ exp[ log[x] ] ]
Вольфрам альфа: интегралы
Как работать с Wolfram Alpha
- Основные операции
- Знаки сравнения
- Логические символы
- Основные константы
- Основные функции
- Решение уравнений
- Решение неравенств
- Решение различных систем уравнений, неравенств и уравнений
- Математический анализ
- Пределы
- Производные
- Интегралы
- Дифференциальные уравнения и их системы
- Ошибки при работе с системой
- Online Systems of Equations Solver
- Solve equations and systems of equations with Wolfram|Alpha
- A powerful tool for finding solutions to systems of equations and constraints
- Tips for entering queries
- Access instant learning tools
- What are systems of equations?
- A system of equations is a set of one or more equations involving a number of variables.
- Системы уравнений в wolfram alpha
- Решение уравнений
- Решение неравенств
- Решение различных систем уравнений, неравенств и уравнений
- Математический анализ
- Пределы
- Производные
- Интегралы
- Дифференциальные уравнения и их системы
- Ошибки при работе с системой
- Partial fraction expansion(1-x^2)/(x^3+x)
- Series expansion at x=0
- Чтобы упростить выражение f[x], наберите команду Simplify[f[x]]
Видео:ТОП приложение для СТУДЕНТОВ в изучении математики! ChatGPT больше не нужен? Эта программа решит всеСкачать

Основные операции
- Сложение
: a+b
- Вычитание
: a-b
- Умножение
: a*b
- Деление
: a/b
- Возведение в степень
: a^b
Примеры
- 314+278; 314—278; 314*278; 314^278;
- (a^2+b^2)+(a^2-b^2); (a^2+b^2)/(a^2-b^2); (a+b)^(2+2/3).
Видео:Wolframalpha : решение любых задач для студента по алгебре, вышке, физике, дифференциальные ур. и прСкачать

Знаки сравнения
- Меньше
: : >
- Равно
: = или ==
- Меньше или равно
: =
Видео:Как решить любую задачу студенту? : Интеллектуальный поисковик wolframalpha.comСкачать

Логические символы
- И
: &&
- ИЛИ
: ||
- НЕ
: !
Видео:Решение уравнений с помощь Solve WolframСкачать

Основные константы
- Число
: Pi
- Число
: E
- Бесконечность
: Infinity, inf или oo
Видео:Научитесь пользоваться WolframAlpha прямо сейчас!Скачать

Основные функции
: x^a
: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
: sin[x] или Sin[x]
: tan[x] или Tan[x]
: cot[x] или Cot[x]
: sec[x] или Sec[x]
: csc[x] или Csc[x]
: ArcCos[x]
: ArcSin[x]
: ArcTan[x]
: ArcCot[x]
: ArcSec[x]
: ArcCsc[x]
: cosh[x] или Cosh[x]
: sinh[x] или Sinh[x]
: tanh[x] или Tanh[x]
: coth[x] или Coth[x]
: sech[x] или Sech[x]
: csch[x] или Csch[е]
: ArcCosh[x]
: ArcSinh[x]
: ArcTanh[x]
: ArcCoth[x]
: ArcSech[x]
: ArcCsch[x]
Видео:[Обзор] Wolfram Alpha - ультимейт система знаний.Скачать
![[Обзор] Wolfram Alpha - ультимейт система знаний.](https://i.ytimg.com/vi/HzNO7jg1U_M/0.jpg)
Решение уравнений
Чтобы получить решение уравнения вида 
Примеры
- Solve[Cos[x]+Cos[2x]+Sin[4x]=0,x] или Cos[x]+Cos[2x]+Sin[4x]=0;
- Solve[x^5+x^4+x+1=0,x] или x^5+x^4+x+1=0;
- Solve[Log[3,x^2+x+1]-Log[9,x^2]=0,x] или Log[3,x^2+x+1]-Log[9,x^2]=0.
Если Ваше уравнение содержит несколько переменных, то запись: f[x, y,…,z]=0 даст весьма разнообразный набор сведений, таких как решение в целых числах, частные производные функции 
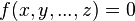

Примеры
- Cos[x+y]=0 или Solve[Cos[x+y]=0,x] или Solve[Cos[x+y]=0,y];
- x^2+y^2-5=0 или Solve[x^2+y^2-5=0,x] или Solve[x^2+y^2-5=0,y];
- x+y+z+t+p+q=9.
Видео:Rec 03 23 22 Решение систем уравнений с использованием Wolfram Д439Скачать

Решение неравенств
Решение в Wolfram Alpha неравенств типа 0″ src=»http://upload.wikimedia.org/math/3/d/9/3d97eb56e02c2889dd20a89529548180.png» />, 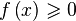

Примеры
- Cos[10x]-1/2>0 или Solve[Cos[10x]-1/2>0,x];
- x^2+5x+10>=0 или Solve[x^2+5x+10>=0,x].
Если Ваше неравенство содержит несколько переменных, то запись: f[x, y,…,z]>0 или f[x, y,…,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x, y,…,z]>0,j] или Solve[f[x, y,…,z]>=0,j], где 
Примеры
- Cos[x+y]>0 или Solve[Cos[x+y]>0,x] или Solve[Cos[x+y]>0,y];
- x^2+y^3-5 =9.
Видео:12.01 Решение систем ДУ в Wolfram MathematicaСкачать

Решение различных систем уравнений, неравенств и уравнений
Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом «И», который в Wolfram Alpha имеет вид &&.
Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида 


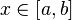


Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:Plot[f[x]&&g[x]&&h[x]&&…&&t[x],].
Для того, чтобы построить график функции 
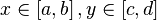


Видео:Вольфрам альфаСкачать

Математический анализ
Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.
Пределы
Для того, чтобы найти предел последовательности 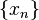
Примеры
- Limit[n^3/(n^4 + 2*n), n -> Infinity];
- Limit[(1+1/n)^n, n -> Infinity].
Найти предел функции 

Производные
Для того, чтобы найти производную функции 



Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Интегралы
Для того, чтобы найти неопределенный интеграл от функции 
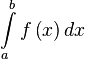
Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Дифференциальные уравнения и их системы
Чтобы найти общее решение дифференциального уравнения 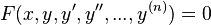
Если Вам требуется решить задачу Коши, то впишите: F[x, y, y’,y»,…], y[s]==A,y'[s]==B, …. Если нужно получить решение краевой задачи, что краевые условия, так же перечисляются через запятую, причем они должны иметь вид y[s]==S.
Решение систем дифференциальных уравнений также просто, достаточно вписать: , где f_1, f_2, …, f_n — дифференциальные уравнения, входящие в систему. К сожалению, решение задач Коши и краевых задач для систем дифференциальных уравнений пока-что не поддерживается.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Ошибки при работе с системой
Система может допускать некоторые ошибки при решении сложных задач [1] . К примеру, если попытаться решить неравенство 
Видео:Wolframalpha решение простейших примеровСкачать

Online Systems of Equations Solver
Видео:Видео курс Wolfram Mathematica | Лин. системы | Часть 1/2Скачать

Solve equations and systems of equations with Wolfram|Alpha
Видео:Как решить задачи по математике онлайнСкачать

A powerful tool for finding solutions to systems of equations and constraints
Wolfram|Alpha is capable of solving a wide variety of systems of equations. It can solve systems of linear equations or systems involving nonlinear equations, and it can search specifically for integer solutions or solutions over another domain. Additionally, it can solve systems involving inequalities and more general constraints.
Learn more about:
Видео:Система уравнений. Метод алгебраического сложенияСкачать

Tips for entering queries
Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about solving systems of equations.
Видео:Using WolframAlpha.com: Step-by-Step Solutions.Скачать

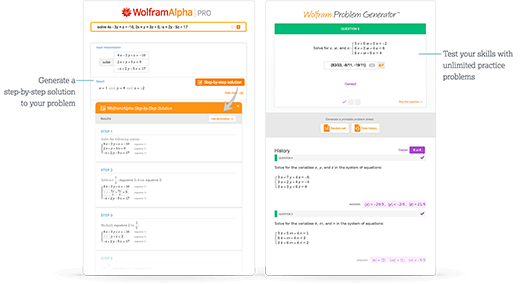
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
Learn more about:
Видео:Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

What are systems of equations?
A system of equations is a set of one or more equations involving a number of variables.
The solutions to systems of equations are the variable mappings such that all component equations are satisfied—in other words, the locations at which all of these equations intersect. To solve a system is to find all such common solutions or points of intersection.
Systems of linear equations are a common and applicable subset of systems of equations. In the case of two variables, these systems can be thought of as lines drawn in two-dimensional space. If all lines converge to a common point, the system is said to be consistent and has a solution at this point of intersection. The system is said to be inconsistent otherwise, having no solutions. Systems of linear equations involving more than two variables work similarly, having either one solution, no solutions or infinite solutions (the latter in the case that all component equations are equivalent).
More general systems involving nonlinear functions are possible as well. These possess more complicated solution sets involving one, zero, infinite or any number of solutions, but work similarly to linear systems in that their solutions are the points satisfying all equations involved. Going further, more general systems of constraints are possible, such as ones that involve inequalities or have requirements that certain variables be integers.
Solving systems of equations is a very general and important idea, and one that is fundamental in many areas of mathematics, engineering and science.
Видео:Решение системы уравнений методом ГауссаСкачать

Системы уравнений в wolfram alpha
: x^a
: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
: sin[x] или Sin[x]
: tan[x] или Tan[x]
: cot[x] или Cot[x]
: sec[x] или Sec[x]
: csc[x] или Csc[x]
: ArcCos[x]
: ArcSin[x]
: ArcTan[x]
: ArcCot[x]
: ArcSec[x]
: ArcCsc[x]
: cosh[x] или Cosh[x]
: sinh[x] или Sinh[x]
: tanh[x] или Tanh[x]
: coth[x] или Coth[x]
: sech[x] или Sech[x]
: csch[x] или Csch[е]
: ArcCosh[x]
: ArcSinh[x]
: ArcTanh[x]
: ArcCoth[x]
: ArcSech[x]
: ArcCsch[x]
- [19.67] =19: integral part of (19.67) — выделяет целую часть числа (integerPart)
Видео:КиЯ 0.18 | Решение уравнения и отображение его корней в Wolfram LanguageСкачать

Решение уравнений
Чтобы получить решение уравнения вида 
Примеры
- Solve[Cos[x]+Cos[2x]+Sin[4x]=0,x] или Cos[x]+Cos[2x]+Sin[4x]=0;
- Solve[x^5+x^4+x+1=0,x] или x^5+x^4+x+1=0;
- Solve[Log[3,x^2+x+1]-Log[9,x^2]=0,x] или Log[3,x^2+x+1]-Log[9,x^2]=0.
Если Ваше уравнение содержит несколько переменных, то запись: f[x, y,…,z]=0 даст весьма разнообразный набор сведений, таких как решение в целых числах, частные производные функции 
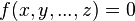

Примеры
- Cos[x+y]=0 или Solve[Cos[x+y]=0,x] или Solve[Cos[x+y]=0,y];
- x^2+y^2-5=0 или Solve[x^2+y^2-5=0,x] или Solve[x^2+y^2-5=0,y];
- x+y+z+t+p+q=9.
Видео:КиЯ 0.4 | Первое знакомство с системой Wolfram MathematicaСкачать

Решение неравенств
Решение в Wolfram Alpha неравенств типа 0″ src=»http://upload.wikimedia.org/math/3/d/9/3d97eb56e02c2889dd20a89529548180.png» />, 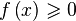

Примеры
- Cos[10x]-1/2>0 или Solve[Cos[10x]-1/2>0,x];
- x^2+5x+10>=0 или Solve[x^2+5x+10>=0,x].
Если Ваше неравенство содержит несколько переменных, то запись: f[x, y,…,z]>0 или f[x, y,…,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x, y,…,z]>0,j] или Solve[f[x, y,…,z]>=0,j], где 
Примеры
- Cos[x+y]>0 или Solve[Cos[x+y]>0,x] или Solve[Cos[x+y]>0,y];
- x^2+y^3-5 =9.
Решение различных систем уравнений, неравенств и уравнений
Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом «И», который в Wolfram Alpha имеет вид &&.
Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида 


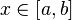


Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:Plot[f[x]&&g[x]&&h[x]&&…&&t[x],].
Для того, чтобы построить график функции 
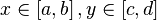


Математический анализ
Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.
Пределы
Для того, чтобы найти предел последовательности 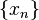
Примеры
- Limit[n^3/(n^4 + 2*n), n -> Infinity];
- Limit[(1+1/n)^n, n -> Infinity].
Найти предел функции 

Производные
Для того, чтобы найти производную функции 



Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Интегралы
Для того, чтобы найти неопределенный интеграл от функции 
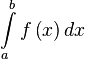
Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Дифференциальные уравнения и их системы
Чтобы найти общее решение дифференциального уравнения 
Если Вам требуется решить задачу Коши, то впишите: F[x, y, y’,y»,…], y[s]==A,y'[s]==B, …. Если нужно получить решение краевой задачи, что краевые условия, так же перечисляются через запятую, причем они должны иметь вид y[s]==S.
Решение систем дифференциальных уравнений также просто, достаточно вписать: , где f_1, f_2, …, f_n — дифференциальные уравнения, входящие в систему. К сожалению, решение задач Коши и краевых задач для систем дифференциальных уравнений пока-что не поддерживается.
Ошибки при работе с системой
Система может допускать некоторые ошибки при решении сложных задач. К примеру, если попытаться решить неравенство 
factor x^2/3 — 3x + 12
и нажимаем равно (=).
Например, разложить на слагаемые
Partial fraction expansion(1-x^2)/(x^3+x)
используются формулы разложения функций в ряд Тейлора (Taylor series) и ряд Маклорена (Maclaurin series) или
Series expansion at x=0
Разложить в ряд Лорана:
Laurent expansion z*cos(1/z) at z =0
Найти вычет функции в точке:
residue of (e^(1/(1-z^2 ))/((1-e^z )* sin(z^2 ) )) at point z = 0
Чтобы упростить выражение f[x], наберите команду Simplify[f[x]]
Комплексно сопряженное z*

 : a+b
: a+b : a-b
: a-b : a*b
: a*b : a/b
: a/b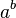 : a^b
: a^b : : >
: : > : = или ==
: = или == : =
: = : &&
: && : ||
: || : !
: ! : Pi
: Pi : E
: E : Infinity, inf или oo
: Infinity, inf или oo
 : x^a
: x^a : Sqrt[x]
: Sqrt[x] : x^(1/n)
: x^(1/n) : a^x
: a^x : Log[a, x]
: Log[a, x] : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x] : sin[x] или Sin[x]
: sin[x] или Sin[x] : tan[x] или Tan[x]
: tan[x] или Tan[x] : cot[x] или Cot[x]
: cot[x] или Cot[x] : sec[x] или Sec[x]
: sec[x] или Sec[x] : csc[x] или Csc[x]
: csc[x] или Csc[x] : ArcCos[x]
: ArcCos[x] : ArcSin[x]
: ArcSin[x] : ArcTan[x]
: ArcTan[x] : ArcCot[x]
: ArcCot[x] : ArcSec[x]
: ArcSec[x] : ArcCsc[x]
: ArcCsc[x] : cosh[x] или Cosh[x]
: cosh[x] или Cosh[x] : sinh[x] или Sinh[x]
: sinh[x] или Sinh[x] : tanh[x] или Tanh[x]
: tanh[x] или Tanh[x] : coth[x] или Coth[x]
: coth[x] или Coth[x] : sech[x] или Sech[x]
: sech[x] или Sech[x] : csch[x] или Csch[е]
: csch[x] или Csch[е] : ArcCosh[x]
: ArcCosh[x] : ArcSinh[x]
: ArcSinh[x] : ArcTanh[x]
: ArcTanh[x] : ArcCoth[x]
: ArcCoth[x] : ArcSech[x]
: ArcSech[x] : ArcCsch[x]
: ArcCsch[x]