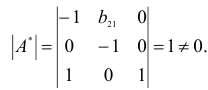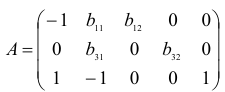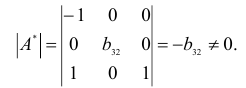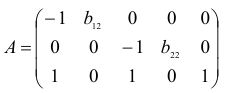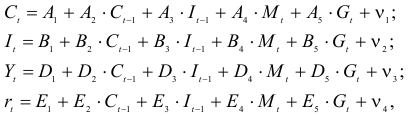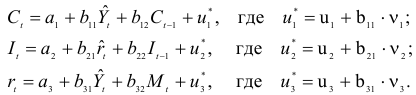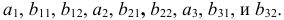Большой объем расчетных математических задач приходится на решение систем линейных алгебраических уравнений. Многие задач управленческого и экономического, технологического характера строятся как линейные алгебраические, либо сводятся к ним.
Актуальность темы заключается в том, что известные приемы и методы решения систем линейных уравнений применимы для решения задач с практическим содержанием, в частности связанных со специальностью «Прикладная информатика в экономике».
Цель работы: рассмотреть различные способы решения систем линейных уравнений, показать примеры их практического применения.
- Скачать:
- Системы эконометрических уравнений
- Эконометрика
- Виды систем эконометрических уравнений
- Проблема идентификации
- Решение эконометрических уравнений
- Пример задачи с уравнением №4.2.1.
- Пример задачи с уравнением №4.2.2.
- Пример задачи с уравнением №4.2.3.
- Пример задачи с уравнением №4.2.4.
- Презентация на тему «Применение систем линейных уравнений для решения прикладных задач»
- Описание презентации по отдельным слайдам:
- 📸 Видео
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| Большой объем расчетных математических задач приходится на решение систем линейных алгебраических уравнений. Многие задач управл | 2.06 МБ |
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
«Яндекс» открыл доступ к нейросети «Балабоба» для всех пользователей
Видео:Решение системы уравнений методом ГауссаСкачать

Системы эконометрических уравнений
Эконометрика как учебная дисциплина на современном этапе благодаря своей универсальности и возможности практического использования для анализа реальных экономических объектов является одним из базовых курсов в системе высшего экономического образования.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Эконометрика
Эконометрика — это статистико-математический анализ экономических отношений.
Сущность эконометрики заключается в модельном описании функционирования конкретной экономической системы (экономики данной страны, спроса-предложения в данное время в данном месте и т.д.). Одним из основных этапов эконометрических исследований является анализ устойчивости построенной модели, отражающей взаимосвязи между экономическими показателями, и проверка ее на адекватность реальным экономическим данным и процессам.
Виды систем эконометрических уравнений
Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений.
Различают несколько видов систем уравнений, применяемых в эконометрике:
• система независимых уравнений — когда каждая зависимая переменная 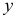
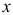
Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый к каждому уравнению в отдельности;
• система рекурсивных уравнений — когда зависимая переменная 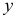
Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый последовательно к каждому уравнению в отдельности;
• система взаимосвязанных (совместных) уравнений — когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а другие в правую:
Такая система уравнений называется структурной формой модели. Для построения таких систем и нахождения их параметров используются косвенный и двухшаговый методы наименьших квадратов.
Возможно эта страница вам будет полезна:
Введем следующие определения:
- Эндогенные переменные — взаимозависимые переменные, которые определяются внутри системы (модели)
.
- Экзогенные переменные — независимые переменные, которые определяются вне системы
.
- Лаговые эндогенные переменные — эндогенные переменные за предыдущие моменты времени.
- Предопределенные переменные — экзогенные и лаговые эндогенные переменные системы.
- Коэффициенты
и
при переменных — структурные коэффициенты модели.
Система линейных функций эндогенных переменных от всех предопределенных переменных системы — приведенная форма модели:
где 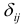
Проблема идентификации
При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация -это единственность соответствия между приведенной и структурной формами модели.
С позиции идентифицируемости структурные модели можно подразделить на три вида:
- идентифицируемые;
- неидентифицируемые;
- сверхидентифицируемые.
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.
Модель еверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы.
Сверхидентифицируемая модель, в отличие от неидентифицируемой, модели практически решаема, но требует для этого специальных методов исчисления параметров.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой.
Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.
Обозначим через 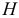
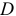
- уравнение идентифицируемо, если
;
- уравнение сверхидентифицируемо, если
;
- уравнение неидентифицируемо, если
.
Если необходимое условие выполнено, то далее проверяется достаточное условие идентификации.
Достаточное условие идентификации — определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Для решения идентифицируемого уравнения применяется косвенный метод наименьших квадратов, для решения сверхидентифицированных -двухшаговый метод наименьших квадратов.
Косвенный МНК состоит в следующем:
• составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
• путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
Двухшаговый МНК заключается в следующем:
• составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
• выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяются двухшаговым МНК, и находят расчетные значения этих эндогенных переменных по соответствующим уравнениям приведенной системы;
• обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части уравнения.
Решение эконометрических уравнений
Пример задачи с уравнением №4.2.1.
Рассматривается модель протекционизма Сальватора (упрощенная версия):
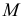
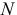
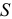
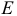
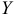
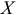
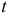
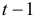
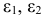
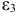
- Применив необходимое и достаточное условие идентификации определить, идентифицировано ли каждое из уравнений модели.
- Определить метод оценки параметров модели.
- Записать приведенную форму модели в общем виде.
Решение:
- Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные 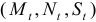
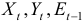
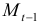
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает три эндогенные переменные 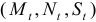
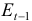
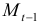
Это уравнение включает три эндогенные переменные 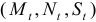
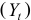
Это уравнение включает три эндогенные переменные 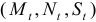
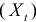
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели:
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее, чем число эндогенных переменных модели минус 1, т.е. в данной задаче больше или равен 3-1=2.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы
Следовательно, для 1 уравнения достаточное условие выполняется, это уравнение точно идентифицируемо. 2 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы
так как она содержит отличный от нуля минор второго порядка
Следовательно, для 2 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо. 3 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы 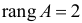
Следовательно, для 3 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо.
- Таким образом, система в целом сверхидентифицируема, для оценки ее параметров можно применить двухшаговый метод наименьших квадратов.
- Запишем приведенную форму модели в общем виде:
Пример задачи с уравнением №4.2.2.
Рассматривается структурная модель вида:
- Применив необходимое и достаточное условие идентификации определить, идентифицировано ли каждое из уравнений модели.
- Определить метод оценки параметров модели.
- Записать приведенную форму модели в общем виде.
- Исходя из приведенной формы модели уравнений
найти структурные коэффициенты модели.
Решение:
- Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные 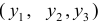
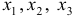
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает две эндогенные переменные ( 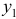
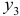
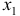
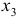
Это уравнение включает три эндогенные переменные 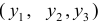
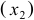
Это уравнение включает две эндогенные переменные (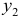
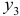
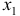
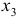
Для этого составим матрицу коэффициентов при переменных модели:
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для первого уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для второго уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для третьего уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
- Все уравнения системы точно идентифицируемы, следовательно, система в целом точно идентифицируема, для оценки ее параметров может быть применен косвенный метод наименьших квадратов.
- Запишем приведенную форму модели в общем виде:
- Вычисление структурных коэффициентов модели:
1) из третьего уравнения приведенной формы выразим 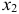
Данное выражение содержит переменные 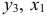
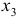
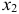
Откуда получим первое уравнение СФМ в виде
2) во втором уравнении СФМ нет переменных 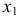

Первый этап: выразим 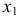
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует 

Подставим его в выражение для
Второй этап: аналогично, чтобы выразить 
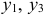
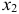

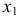
Подставим полученные 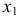

В результате получаем второе уравнение СФМ
3) из второго уравнения ПФМ выразим 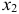
Подставим полученное выражение в третье уравнение ПФМ
В результате получаем третье уравнение СФМ
Таким образом, СФМ примет вид
Пример задачи с уравнением №4.2.3.
Изучается модель вида
где 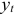
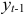
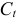
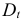
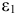
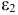
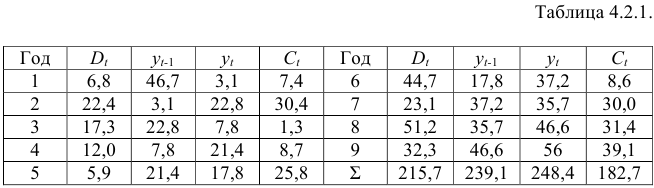
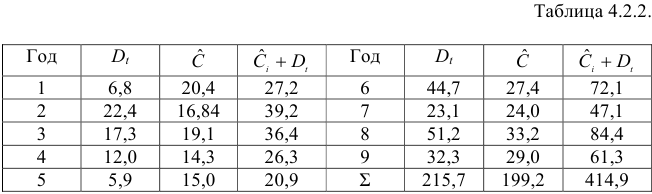
Информация за девять лет о приросте всех показателей дана в таблице 4.2.1.
Для данной модели была получена система приведенных уравнений
- Применив необходимое и достаточное условие идентификации, определить, идентифицировано ли каждое из уравнений модели.
- Рассчитать параметры первого уравнения структурной модели.
Решение:
- В данной модели две эндогенные переменные (
и
) и две экзогенные переменные (
и
). Второе уравнение точно идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равенство: 2=1 + 1.
Первое уравнение сверхидентифицировано, так как в нем на параметры при 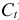
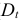
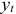
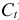
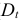
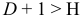
- Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.
Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной 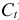
подставим значения 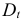
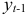
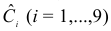
Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения 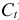
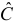
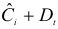
Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную 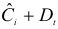
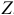
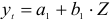
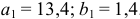
Пример задачи с уравнением №4.2.4.
Рассматривается следующая модель:
— расходы на потребление в период
;
— совокупный доход период
:
— инвестиции в период
;
— процентная ставка в период
;
— денежная масса в период
;
— государственные расходы в период
;
— расходы на потребление в период
;
— инвестиции в период
;
— текущий период;
— предыдущий период;
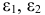
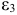
В предположении, что имеются временные ряды данных по всем переменным модели, предложить способ оценки ее параметров.
Как изменится ваш ответ на вопрос п. 1, если из модели исключить тождество дохода?
Решение:
- Модель представляет собой систему одновременных уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает четыре эндогенные переменные 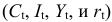
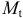
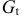
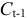
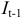
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает две эндогенные переменные ( 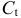
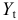
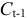
Это уравнение включает две эндогенные переменные 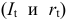
3-е уравнение тоже включает две эндогенные переменные 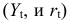
Это уравнение представляет собой тождество, параметры которого известны. Необходимости в его идентификации нет.
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее числа эндогенных переменных модели минус 1, т. е. 4-1=3.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ее ранг равен 3, так как определитель квадратной подматрицы 3×3 этой матрицы не равен нулю
Достаточное условие идентификации для 1-го уравнения выполняется.
Выпишем матрицу коэффициентов при переменных, не входящих в уравнение
Ее ранг равен 3, так как определитель квадратной подматрицы 3×3 этой матрицы не равен нулю
Достаточное условие идентификации для 2-го уравнения выполняется.
Выпишем матрицу коэффициентов при переменных, не входящих в уравнение
Ее ранг равен трем, так как имеется квадратная подматрица 3×3 этой матрицы, определитель которой не равен нулю.
Достаточное условие идентификации для 3-го уравнения выполняется.
Таким образом, все уравнения модели сверхидентифицированы. Для оценки параметров каждого из уравнений будем применять двухшаговый МНК.
Шаг 1. Запишем приведенную форму модели в общем виде
где 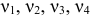
Определим параметры каждого из приведенных выше уравнений в отдельности обычным МНК. Затем найдем расчётные значения эндогенных переменных 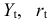
Шаг 2. В исходных структурных уравнениях заменим эндогенные переменные, выступающие в качестве факторных признаков, их расчетными значениями
Применяя к каждому из полученных уравнений в отдельности обычный МНК, определим структурные параметры
Если из модели исключить тождество дохода, число предопределенных переменных модели уменьшится на 1 (из модели будет исключена переменная 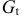
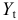
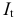
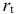
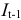
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Матричный метод решения систем уравненийСкачать

Презентация на тему «Применение систем линейных уравнений для решения прикладных задач»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
ГПОУ «Донецкий политехнический колледж» Применение систем линейных уравнений для решения прикладных задач. Прелодаватель математики Низамова И . В. Донецк 2018
Математика – царица наук Карл Фридрих Гаусс
Системы линейных уравнений широко используются в задачах экономики, физики, электротехники, программирования и других наук.
Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных. Система линейных уравнений с n переменными:
Числа aij (i=1,2,…,m, j=1,2,…,n) называются коэффициентами при переменных, а bi (i=1,2,…,m) – свободными членами. Решение системы уравнений — это последовательность чисел (k1, k2, . kn), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x1, x2. xn дает верное числовое равенство.
Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной. Методы решения: По формулам Крамера; Исключение неизвестных ( метод Гаусса); С помощью обратной матрицы.
Метод Крамера Если главный определитель системы то система имеет единственное решение, которое можно найти по формулам Крамера: где –определитель, полученный из главного заменой i-того столбца столбцом свободных членов.
Метод Гаусса Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. Расширенная матрица содержит вместе с коэффициентами при неизвестных свободные члены системы уравнений.
Матричный метод Cистему линейных уравнений записывают в матричной форме: AX = B, где A — основная матрица системы; B — столбец свободных членов; X — столбцы решений системы; Матричное уравнение умножают слева на A–1 (матрицу, обратную к матрице A). Так как A− 1A = E, то X = A -1B. Метод применим, если определитель системы не равен 0.
Проверка домашнего задания Решить систему линейных уравнений всеми известными методами
Применение систем линейных уравнений для решения прикладных задач. Цель занятия: формировать умение составлять системы линейных уравнений по текстовому условию задачи; закрепить применение методов Крамера и Гаусса решения систем линейных уравнений.
Доклад №1. Задача по электротехнике Два источника постоянного тока соединены параллельно, имеют E1=11,5 B, r1=2,5 Oм, E1=16,5 B, r1=6 Oм, и нагрузочный резистор сопротивлением Rн=30 Oм. Определить значения и направление токов через источники и нагрузку.
В соответствии со вторым законом Кирхгофа Для контура, включающего в себя два источника и имеем: Для контура с источником и сопротивлением нагрузки при обходе по часовой стрелке имеем: Подставив числовые данные, получим:
Первое уравнение умножим на 6 и сложим со вторым и третьим. Получим: второе уравнение умножим на (-6) и сложим с третьим. Получим: Отсюда
Доклад №2. Из Москвы в Казань необходимо перевезти оборудование трех типов: I типа — 95 ед., II типа — 100 ед., III типа — 185 ед. Для перевозки оборудования завод может заказать три вида транспорта. Количество оборудования каждого типа, вмещаемого на определенный вид транспорта, приведено в таблице. Установить, сколько единиц транспорта каждого вида потребуется для перевозки этого оборудования. Тип оборудования Количество оборудования Т1 Т2 Т3 I 3 2 1 II 4 1 2 III 3 5 4
Пусть x ‒ количество единиц I-ого вида транспорта, y ‒ количество единиц II-ого вида транспорта, z ‒ количество единиц III-его вида транспорта. Тогда Решим систему уравнений методом Крамера: Δ = =12+12+20-3-30-32=-21 ; Δх = =380+740+500-185-950-800=-315; х = = 15;
Δу = =1200+570+740-300-1110-1520=-420; у = = 20; Δz = =555+600+1900-285-1500-1480=-210; Z = = 10. Ответ: Транспорта I-ого вида использовано 15 единиц, II-ого вида 20 единиц, а III-го вида 10 единиц.
Доклад №3. Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице: Найти количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. Тип заготовки Способ раскроя 1 2 3 А 3 2 1 Б 1 6 2 В 4 1 5
Обозначим через x, y, z количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. По условию задачи составим систему уравнений:
Ответ: первым способом раскраивается 90 листов, вторым – 15, третьим – 60.
Доклад №4. Частным лицом куплены три пакета акций общей стоимостью 485 ден. ед., причем акции первой группы куплены по 5 ден. ед. за акцию, второй – по 20, третьей – по 13. Через месяц стоимость акций первой, второй и третьей групп составила соответственно 6, 14 и 19 ден. ед., а стоимость всего пакета была 550 ден. ед. Еще через месяц они стоили по 8, 22 и 20 ден. ед. соответственно, а весь пакет стоил 660 ден. ед. Cколько акций каждой группы было куплено?
Пусть акции I-ой группы было куплено х штук, акций II-ой группы y штук, акций III-ей группы z штук. Согласно условию задачи имеем: Решим систему уравнений методом Крамера: Δ = = = 1400+3040+1716-1456-2090-2400=210;
= = 135800+250800+157300-120120-202730-220000=1050; = = 55000+73720+51480-57200-62700-58200=2100; = = 46200+88000+64020-54320-60500-79200=4200; x = = 5; y = = 10; z = = 20; Ответ: Акций I-й группы было куплено 5 штук, акций II-ой группы было куплено 10 штук, акций III-ей группы было куплено 20 штук.
Карл Фридрих Гаусс Карл Фридрих Гаусс родился 30 апреля 1777 г. Гаусс с детства проявлял все признаки гениальности. Главный труд всей своей жизни, «Арифметические исследования», юноша закончил ещё в 1798 г. В 1799 г. Гаусс заочно защищает диссертацию. Самым знаменитым трудом, проделанным Карлом Фридрихом Гауссом, была работа под названием «Теория движения небесных тел». Именно в ней ученый предложил теорию возмущения орбит. Знаменитая теорема алгебры, термин «гауссова кривизна», основы дифференциальной геометрии вошли в основу фундаментальных математических законов.
Габриэль Крамер Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария) в семье врача. Уже в детстве он опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики. В 18 лет он успешно защитил диссертацию. Талантливый учёный написал множество статей на самые разные темы: геометрия, история, математика, философия. В 1730 году он опубликовал труд по небесной механике. Крамер является одним из создателей линейной алгебры. В работе «Введение в анализ алгебраических кривых» Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера.
Закрепление нового материала. Задача №1. Рассчитать сложную электрическую цепь, если E1=246 B, R1=0,3 Ом, E2=230 B, R2=1 Ом, R3=24 Ом, RВТ1= RВТ2=0.
Задача №2. Предприятием по производству бытовой техники в 1 квартале выпущено 4000 вентиляторов, 2000 миксеров и 6000 электрочайников на общую сумму 23 млн рублей. Во 2 квартале выпущено 3000 вентиляторов, 1000 миксеров и 4000 электрочайников на общую сумму 15,6 млн рублей. В 3 квартале выпущено 1000 вентиляторов, 3000 миксеров и 1000 электрочайников на общую сумму 7,8 млн рублей. Найти стоимость одного вентилятора, одного миксера и одного электрочайника.
Рефлексия Выберите смайлик, характеризующий ваше состояние на занятии.
Домашнее задание. Если ширину производственной прямоугольной площадки увеличить на 4 м, а ее длину уменьшить на 2 м, то ее площадь увеличится на 32 ; если же ширину уменьшить на 3 м, а длину увеличить на 1 м, то ее площадь уменьшится на 39 . Найдите длину и ширину площадки.
📸 Видео
Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение системы уравнений методом Крамера.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Задание №20. Экзамен ОГЭ. Система уравнений #shortsСкачать

Система уравнений. Метод алгебраического сложенияСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Математика это не ИсламСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Решение системы уравнений в ExcelСкачать

симметрические системы уравненийСкачать

Решение систем уравнений методом подстановкиСкачать

Системы уравнений Тема5 Решения задач составлением системы уравнений.Скачать

Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Необычное решение типичной системы уравненийСкачать



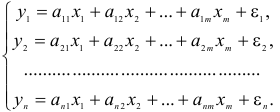
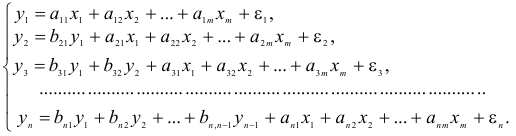
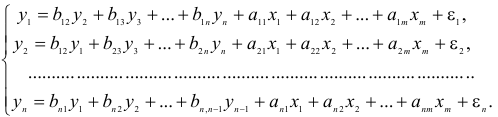
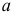 и
и 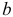 при переменных — структурные коэффициенты модели.
при переменных — структурные коэффициенты модели.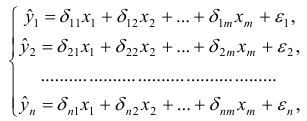
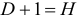 ;
;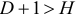 ;
;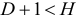 .
.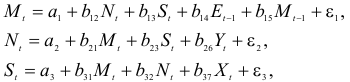

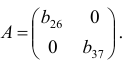
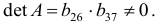
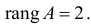
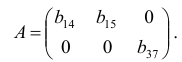
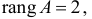
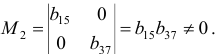
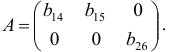
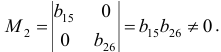
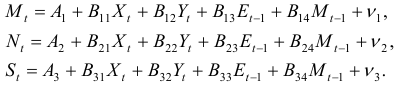
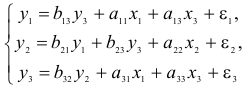
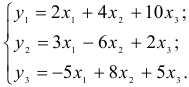

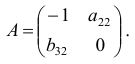
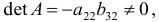
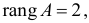
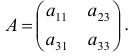
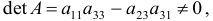
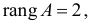
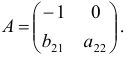
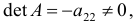
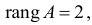
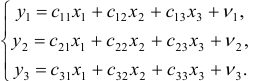
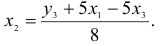
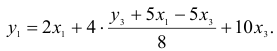
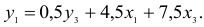
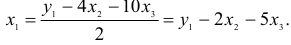
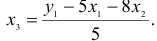
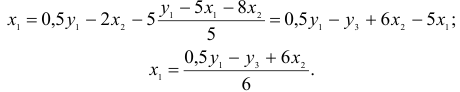
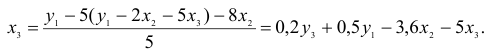
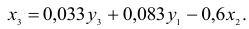
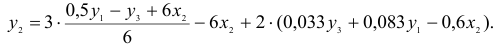
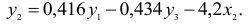
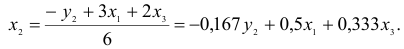
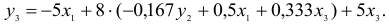
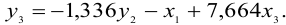
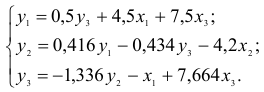
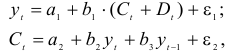
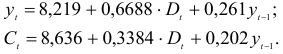
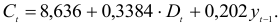
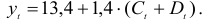
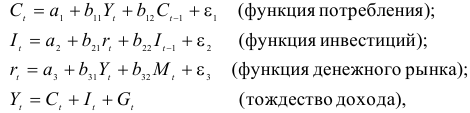
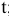 ;
;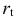 — процентная ставка в период
— процентная ставка в период 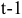 ;
;