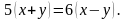Системы уравнений с двумя переменными задачи на движение

Видео:Задачи на движение | Математика TutorOnlineСкачать

Решение задач с использованием систем линейных уравнений с двумя переменными.

Данная разработка предназначена для учеников 7 класса, а также для тех, кто желает отработать навык решения задач. Теоретическая часть содержит примеры решения задач с использованием систем уравнений. В практической части представлено большое количество задач с тематическим разделением.

Просмотр содержимого документа
«Решение задач с использованием систем линейных уравнений с двумя переменными.»

Решение задач с использованием систем линейных уравнений с двумя переменными.

Переходим теперь к практическому применению систем линейных уравнений с двумя переменными. Часто бывает, что в задачах неизвестны два, а то и три-четыре компонента. И в этом случае обозначение какого-то одного компонента переменной не облегчает решение задачи. Тогда нужно ввести две или три переменные. Вот здесь нам как раз и понадобится система уравнений и способы её решения. Приведём пример с полным описанием.

Например, решить задачу. Лодка за 3 ч движения по течению и 4 ч против течения проходит 114 км. Найдите скорость лодки по течению и её скорость против течения, если за 6 ч движения против течения она проходит такой же путь, как за 5 ч по течению.

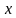
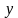
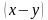
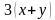
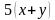
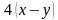
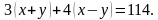
Решение. В задаче описывается движение по воде. А значит, должна быть собственная скорость лодки и скорость течения реки. Они нам и не известны, поэтому обозначим через км/ч собственную скорость лодки, а через км/ч – скорость течения реки. Тогда скорость лодки по течению реки равна км/ч, а скорость лодки против течения реки — км/ч. За 3 ч движения по течению реки лодка пройдёт км, а за 5 ч — км. За 4 ч против течения лодка пройдёт км, а за 6 ч — км. По условию задачи известно, что за 3 ч по течению и 4 ч против течения лодка пройдёт всего 114 км, значит, составляем первое уравнение: Также по условию задачи известно, что за 6 ч движения против течения лодка проходит такой же путь, что и за 5 ч по течению, поэтому составляем второе уравнение:

Для наглядности составим условие задачи в виде таблицы.

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Презентация по алгебре. Тема: «Решение задачи на движение с помощью системы уравнений с двумя переменными (способом подстановки), 9 классс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Описание презентации по отдельным слайдам:

Презентация Ибрагима Маербиева «Нестандартное решение задачи из ай – школы с помощью систем уравнений» Учитель математики: Албогачиева Радима Руслановна РЦДО 25 февраля 2016 года

Задача на движение Формула S = v*t , S — это расстояние, v-это скорость, t — это время движения

Задание «Решение задач на движение» Задача №3

ай-школа Тема 7 » Из двух городов, расстояние между которыми равно 270 км, одновременно навстречу друг другу выходят два поезда и встречаются через 3 ч. На весь путь один из поездов тратит на 1 ч 21 мин больше, чем другой. Найдите скорость каждого поезда.

Краткая запись и чертеж: 1 2 S=270 км V1=х v2=у S1= v*t=3х S2= v*t=3у Значит, можно найти S = v*t

3х+3у=270 — Это первое уравнение, которое у нас получилось Теперь, зная, что разница во времени 1 ч 21 мин=121/60 = 1,35, можем составить второе уравнение

S = v* t t=S/v 270/x — 270/y= 121/60 = 1,35 t1= 270/x и t2= 270/y

3х+3у=270обе части 1 уравнения сократим на 3, 270/x — 270/y 1,35 2ур — на 9 и получим Решение: Объединим уравнения и получим систему уравнений, которую удобнее решить методом подстановки:

х =90-у 30/ (90-у) — 30/y=0,15 х+у=90 выразим х через у х =90-у и подставим во 2 уравнение 30/x — 30/y=0,15 получим

Теперь отдельно рассмотрим второе уравнение 30/ (90-у) — 30/y=0,15 умножим на общий знаменатель обе части уравнения и получим: 30 y -270+30у-13,5у+0,15у2=0 0,15у2 +46,5у -270=0 разделим на 3 0,5 у2+15,5у — 90=0получили квадратное ур где а=0,5 ; в= 15,5 ; с= -90 Д= в2 – 4ас= 240,25 + 180=420,25 > 0 (2 корня) √Д= 20,5

у1= (15,5+20,5)/ (2*0,5)=36/1=36 у2= (15,5-20,5)/ (2*0,5)=-5/1=-5

Краткое описание документа:

Презентация Ибрагима Маербиева «Нестандартное решение задачи из ай – школы с помощью систем уравнений» Учитель математики: Албогачиева Радима Руслановна РЦДО 25 февраля 2016 года Задача на движение Формула S = v*t , S — это расстояние, v-это скорость, t — это время движения Задание «Решение задач на движение» Задача №3 ай-школа Тема 7 » Из двух городов, расстояние между которыми равно 270 км, одновременно навстречу друг другу выходят два поезда и встречаются через 3 ч. На весь путь один из поездов тратит на 1 ч 21 мин больше, чем другой. Найдите скорость каждого поезда. Краткая запись и чертеж: 1 2 S=270 км V1=х v2=у S1= v*t=3х S2= v*t=3у Значит, можно найти S = v*t 3х+3у=270 — Это первое уравнение, которое у нас получилось Теперь, зная, что разница во времени 1 ч 21 мин=121/60 = 1,35, можем составить второе уравнение S = v* t t=S/v 270/x — 270/y= 121/60 = 1,35 t1= 270/x и t2= 270/y 3х+3у=270обе части 1 уравнения сократим на 3, 270/x — 270/y 1,35 2ур — на 9 и получим Решение: Объединим уравнения и получим систему уравнений, которую удобнее решить методом подстановки: х =90-у 30/ (90-у) — 30/y=0,15 х+у=90 выразим х через у х =90-у и подставим во 2 уравнение 30/x — 30/y=0,15 получим Теперь отдельно рассмотрим второе уравнение 30/ (90-у) — 30/y=0,15 умножим на общий знаменатель обе части уравнения и получим: 30 y -270+30у-13,5у+0,15у2=0 0,15у2 +46,5у -270=0 разделим на 3 0,5 у2+15,5у — 90=0получили квадратное ур где а=0,5 ; в= 15,5 ; с= -90 Д= в2 – 4ас= 240,25 + 180=420,25 > 0 (2 корня) √Д= 20,5 у1= (15,5+20,5)/ (2*0,5)=36/1=36 у2= (15,5-20,5)/ (2*0,5)=-5/1=-5

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Решение текстовых задач. 9-й класс

Разделы: Математика

Класс: 9

1. Совершенствование навыков решения текстовых задач.
2. Продолжить формирование знаний учащихся по решению систем уравнений с двумя неизвестными.
3. Развитие математической грамотности.

1. Актуализация знаний учащихся (5 минут).

1. Найдите решение системы уравнений:

Ответы: 1) (1;3); 2) (0;3); 3) (1;2); 4) (2;1).

2. Выразите из уравнения 3х + 2у = 5 переменную х через переменную у.

1)

2)

2. Объяснение нового материала (8 минут).

Алгоритм решения задач на движение и на производительность:

1. Ввести неизвестные величины.
2. Составить краткую запись задачи в таблице (скорость, путь, время) или (производительность, работа, время).
3. Исходя из условия задачи, составить систему двух уравнений с двумя неизвестными.
4. Решить систему уравнений, исключив те корни, которые не подходят по условию задачи.
5. Записать ответ по вопросу задачи.

Расстояние между двумя пристанями 60 км. Теплоход проходит это расстояние по течению и против течения за 5,5 часов. Найдите скорость теплохода в стоячей воде и скорость течения, если одна из них больше другой на 20 км/ч.

Краткая запись: пусть скорость теплохода х км/ч, а скорость течения реки у км/ч, тогда

Зная, что теплоход проходит это расстояние по течению и против течения реки за 5,5 часов и скорость катера больше скорости течения реки, составим систему двух уравнений с двумя неизвестными:

Ответ: 22 км/ч – скорость теплохода, 2 км/ч – скорость течения реки.

3. Решение задач (30 минут).

Фермер отправился на машине в город, находящийся на расстоянии 110 км от фермы. Через 20 минут из города на ферму выехал его сын, который проезжал в час на 5 км больше. Встреча произошла в 50 км от города. С какой скоростью ехал фермер?

Краткая запись: пусть скорость фермера х км/ч, а скорость сына у, тогда

Зная, что встреча произошла в 50 км от города, и сын выехал на 20 минут позже, составим систему уравнений с двумя неизвестными:

Второе решение не подходит по условию задачи.

Ответ: 45 км/ч скорость фермера.

Расстояние в 360 км легковой автомобиль прошел на 2 часа быстрее, чем грузовой. Если скорость каждого автомобиля увеличить на 30 км/ч, то грузовой затратит на весь путь на 1 час больше, чем легковой. Найдите скорость каждого автомобиля.

Краткая запись: пусть скорость легкового автомобиля х км/ч, а скорость грузового у км/ч, тогда:

Зная, что в первом случае легковой автомобиль приезжает на 2 часа раньше, а во втором на 1 час раньше, составим систему уравнений с двумя переменными:

Ответ: 90 км/ч скорость легкового автомобиля, 60 км/ч скорость грузового автомобиля.

Бассейн наполнится. Если первую трубу открыть на 12 минут, а вторую – на 7 минут. Если же обе трубы открыть на 6 минут. То наполнится 2/3 бассейна. За сколько минут наполнится бассейн, если открыть только вторую трубу?

Краткая запись: пусть весь объем воды в бассейне равен 1, производительность 1 трубы х , а второй – у, тогда:

Зная, что в первом случае бассейн наполнится полностью, а во втором только 2/3, составим систему двух уравнений с двумя неизвестными.

Ответ: за 15 минут вторая труба заполнит весь бассейн.

Двое рабочих могут выполнить задание за 12 дней. Если сначала один из них сделает половину всей работы, а потом остальное сделает другой, то им потребуется 25 дней. За сколько дней каждый рабочий, работая один, может выполнить задание?

Краткая запись: пусть производительность 1 рабочего х, а второго у, тогда:

Зная, что вместе они сделают работу за 12 дней, а работая по очереди и выполнив по половине работы, им потребуется 25 дней, составим систему уравнений с двумя неизвестными:

Ответ: один рабочий выполнит всю работу за 30 дней, а другой за 20 дней.

4. Подведение итогов урока (2 минуты).

Домашнее задание: п. 22, №476, 479, 491.

1. Учебник «Алгебра 9», автор Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е.

📺 Видео

Задачи на движение по воде | Математика | TutorOnlineСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение задач на движение с помощью систем линейных уравнений с двумя переменнымиСкачать

Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать

ОГЭ Задание 22 Задача на движение Система уравненийСкачать

ЕГЭ задание 11 Задача на движение двух велосипедистов Система уравненийСкачать

Математика | ЗАДАЧА 22 из ОГЭ. Задачи на работуСкачать

Решение задач с помощью систем уравнений второй степени. Алгебра, 9 классСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

№32.11 Решение задачи на движение с помощью системы уравненийСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

ОГЭ Задание 22 Задача на движение Система уравненийСкачать

Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Системы уравнений с двумя переменными. Алгебра 9 классСкачать

Задание 21 ОГЭ Текстовая задача на движение. Система уравнений с 2 неизвестными. Подготовка к ОГЭ.Скачать