Системы уравнений с двумя переменными в знаменателе (8 видео)

Методы решения систем уравнений с двумя переменными

Содержание

п.1. Метод подстановки
п.2. Метод сложения
п.3. Метод замены переменных
п.4. Графический метод
п.5. Примеры
Системы уравнений с двумя переменными, способы решения
Способ подстановки
Способ сложения.
Готовые работы на аналогичную тему
Графический способ
Способ введения новых переменных
Системы линейных уравнений с двумя переменными. Часть 1. Метод подстановки для решения системы линейных уравнений с двумя переменными
📸 Видео

п.1. Метод подстановки

Вариант 1
Шаг 1. Из одного уравнения выразить y через x: y(x).
Шаг 2. Подставить полученное выражение во второе уравнение и найти x.
Шаг 3. Подставить найденный x в y(x) и найти y.
Шаг 4. Записать полученные пары решений. Работа завершена.

Вариант 2
Шаг 1. Из одного уравнения выразить x через y: x(y).
Шаг 2. Подставить полученное выражение во второе уравнение и найти y.
Шаг 3. Подставить найденный y в x(y) и найти x.
Шаг 4. Записать полученные пары решений. Работа завершена.

п.2. Метод сложения

п.3. Метод замены переменных

Иногда удобно ввести новые переменные и решить систему для них.
А затем, вернуться к исходным переменным и найти их значения.

п.4. Графический метод

Графический метод подробно рассмотрен в §15 данного справочника.

п.5. Примеры

Пример 1. Решите систему уравнений:
а) ( left< begin mathrm & \ mathrm & endright. )
Решаем методом подстановки: ( left< begin mathrm & \ mathrm & endright. )
Для нижнего уравнения: ( mathrm )
Подставляем в верхнее уравнение: ( mathrm )

б) ( left< begin mathrm & \ mathrm & endright. )
Замена переменных: ( left< begin mathrm & \ mathrm & endright. )
Выразим (x 2 + y 2 ) через a и b:
x 2 + y 2 = (x 2 + y 2 + 2xy) – 2xy = (x + y) 2 – 2xy = a 2 – 2b
Подставляем: ( left< begin mathrm & \ mathrm & endright.Rightarrow left< begin mathrm & \ mathrm & endright. )
Решаем нижнее уравнение: 2b 2 – 9b + 10 = 0 $$ mathrm< D=9^2-4cdot 2cdot 10=1, b=frac> = left[begin mathrm & \ mathrm & endright. $$ Возвращаемся к исходным переменным: ( left[begin left<begin mathrm & \ mathrm & endright.& \ left<begin mathrm & \ mathrm & endright. endright. )

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Системы уравнений с двумя переменными, способы решения

Вы будете перенаправлены на Автор24

Напомним для начала определение решения системы уравнений с двумя переменными.

Пара чисел называется решением системы уравнений с двумя переменными, если при их подстановки в уравнение получается верное равенство.

В дальнейшем будем рассматривать системы из двух уравнений с двумя переменными.

Существуют четыре основных способа решения систем уравнений: способ подстановки, способ сложения, графический способ, способ ведения новых переменных. Рассмотрим эти способы на конкретных примерах. Для описания принципа использования первых трех способов будем рассматривать систему двух линейных уравнений с двумя неизвестными:

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Способ подстановки

Способ подстановки заключается в следующем: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$

Выразим из второго уравнения $y$ через $x$:

Подставим в первое уравнение, найдем $x$:

Ответ: $(-2, 3)$

Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Способ сложения.

Рассмотрим данный способ на примере:

Умножим второе уравнение на 3, получим:

Теперь сложим оба уравнения между собой:

Найдем $y$ из второго уравнения:

Ответ: $(-2, 3)$

. Отметим, что в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении одна из переменных «исчезла».

Готовые работы на аналогичную тему

Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать

Графический способ

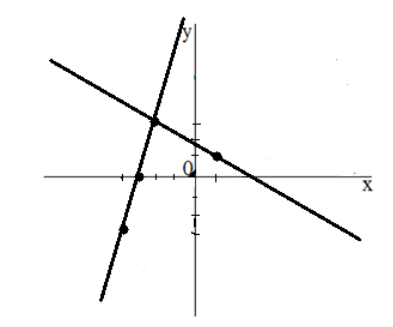
Графический способ заключается в следующем: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.

Выразим из обоих уравнений $y$ через $x$:

Изобразим оба графика на одной плоскости:

Ответ: $(-2, 3)$

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Способ введения новых переменных

Этот способ рассмотрим на следующем примере:

Решение.

Данная система равносильна системе

Пусть $2^x=u (u>0)$, а $3^y=v (v>0)$, получим:

Решим полученную систему методом сложения. Сложим уравнения:

Тогда из второго уравнения, получим, что

Возвращаясь к замене, получим новую систему показательных уравнений:

Ответ: ($0,1$).

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 08 04 2021

Видео:Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

Системы линейных уравнений с двумя переменными. Часть 1. Метод подстановки для решения системы линейных уравнений с двумя переменными

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Мы научились составлять математическую модель для решения различных прикладных задач. В результате задача сводится к технике – решению уравнения или системы уравнений. На этом уроке мы научимся решать системы уравнений, а именно системы линейных уравнений с двумя переменными.