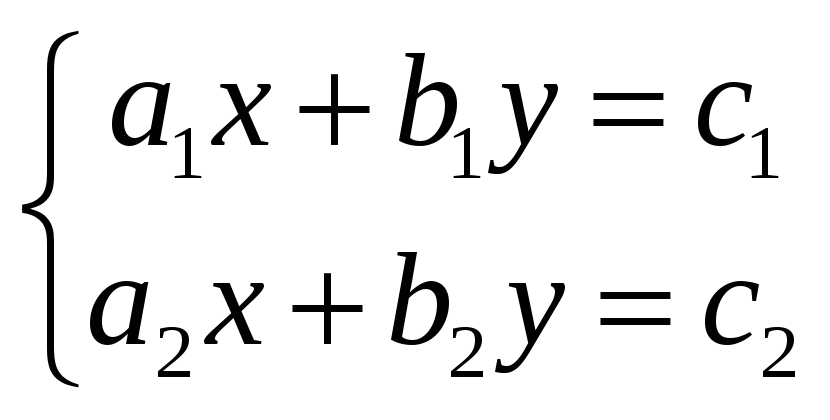Системы уравнений с двумя неизвестными 7 класс никольский конспект урока

Видео:Алгебра 7 класс (Урок№46 - Системы двух уравнений первой степени с двумя неизвестными.)Скачать

Алгебра. 7 класс

Конспект урока

Системы двух уравнений первой степени с двумя неизвестными

Перечень рассматриваемых вопросов:

• Линейные уравнения.
• Корень уравнения;
• Решение линейных уравнений.

Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.

Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.

Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.

Свободный член – член уравнения, не содержащий неизвестного.

Решить уравнение – значит найти все его корни или установить, что их нет.

Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.

Решить систему это значит найти все её решения.

Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.

Решение данной системы всякая пара значений неизвестных, удовлетворяющая обоим уравнениям, образующим систему.

Если отыскиваются общие решения двух или нескольких уравнений, то говорят, что эти уравнения образуют систему.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Пусть даны 2 уравнения с двумя неизвестными, например: x + 2y = 15 и x + 2y = 7.

Каждое из них имеет бесконечное множество решений. Поставим вопрос: среди всех этих решений не будут ли общие для обоих уравнений?

Такие общие решения могут быть, а могут и не быть. Так, общим решением данных уравнений будет то, что легко проверить подстановкой. (Дальше будет показано, что других общих решений эти уравнения иметь не могут).

Но, уравнения не имеют ни одного общего решения. В самом деле, какие бы значения мы ни подставляли, при любых x и y выражение x + 2y не может одновременно равняться 15 и 7. Поэтому ни одно решение первого уравнения не может быть решением второго и ни одно решение второго уравнения не может быть решением первого.

Если отыскиваются общие решения двух или нескольких уравнений, то говорят, что эти уравнения образуют систему.

Всякая пара значений неизвестных, удовлетворяющая обоим уравнениям, образующим систему, называется решением данной системы.

Решить систему это значит найти все её решения.

Решать системы двух уравнений можно с помощью:

• способа подстановки;
• способа уравнивания коэффициентов.

Способ подстановки состоит в том, что:

1) из одного уравнения мы находим выражение одного из неизвестных, например x, через известные величины и другое неизвестное у;

2) найденное выражение подставляем во второе уравнение, в котором после этой подстановки будет содержаться только одно неизвестное у;

3) решаем полученное уравнение и находим значение у;

4) подставляя найденное значение у в выражение неизвестного x, найденное в начале решения, получаем значение х.

Способ уравнивания коэффициентов:

1) обе части одного уравнения умножаются на некоторый множитель; обе части второго уравнения умножаются на другой множитель. Эти множители подбираются так, чтобы коэффициенты при одном из неизвестных в обоих уравнениях после их умножения на эти множители имели одну, и ту же абсолютную величину;

2) складываем два уравнения или вычитаем их друг из друга, смотря по тому, имеют ли уравненные коэффициенты различные или одинаковые знаки; этим одно из неизвестных исключается;

3) решаем полученное уравнение с одним неизвестным;

4) другое неизвестное можно найти тем же приемом, но обычно, проще всего, подставить найденное значение первого неизвестного в любое из данных уравнений и решить получившееся уравнение с одним неизвестным.

В элементарной математике рассматривают только некоторые простые частные случаи систем уравнений второй или высшей степени. Такова в частности, система

Разбор заданий тренировочного модуля

Решим систему, используя метод уравнивания коэффициентов. В данной системе коэффициенты уже уравнены, потому просто сложим почленно оба уравнения, получаем:

Задание 2. Какие значения переменных удовлетворяют системе уравнений:

Решим данную систему, используя метод уравнивания коэффициентов. В данной системе коэффициенты уже уравнены, потому просто вычтем почленно из первого уравнения второе, получаем:

Видео:Урок по теме СПОСОБ ПОДСТАНОВКИ 7 классСкачать

Урок алгебры в 7 классе на тему «Системы двух уравнений первой степени с двумя неизвестными»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

6. Тема и номер урока в теме

Сахокия Дильбар Абдумавлоновна

МОУ Гимназия №1 г. Ярославля

Системы двух уравнений первой степени с двумя неизвестными

Алгебра. 7 класс: учебник для общеобразоват. организаций/ ( С.М. Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин).- 3-е изд. -М.: Просвещение, 2016.- 287 с.: ил. – (МГУ – школе).

приобретение новых знаний с использованием ранее изученного материала при решении систем двух уравнений первой степени с двумя неизвестными , выработка умений и навыков в решении систем уравнений методом подстановки, их применение к решению систем двух уравнений первой степени с двумя неизвестными и решению задач.

9. Планируемые результаты:

предметные: уметь в процессе реальной ситуации использовать навыки решения систем двух уравнений первой степени с двумя неизвестными

личностные: умение работать в парах, слушать собеседника и вести диалог, аргументировать свою точку зрения

метапредметные: уметь обрабатывать информацию; формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности

10. Задачи урока:

образовательные (формирование познавательных УУД): обеспечить осознанное усвоение способа подстановки при решении систем двух уравнений первой степени с двумя неизвестными; закрепить навыки и умения применять алгоритмы при решении систем двух уравнений первой степени с двумя неизвестными, создание условий для систематизации, обобщения и углубления знаний учащихся при решении систем двух уравнений первой степени с двумя неизвестными.

воспитательные (формирование коммуникативных и личностных УУД): формировать умение слушать и вступать в диалог, внимательность и аккуратность в вычислениях; воспитывать чувство взаимопомощи, уважительное отношение к чужому мнению, культуру учебного труда, требовательное отношение к себе и своей работе.

развивающие (формирование регулятивных УУД): способствовать развитию творческой активности учащихся; повысить познавательный интерес к предмету; развитие навыков и способностей критического мышления (навыков сопоставления, формулирования и проверки гипотез — правил решения систем уравнений, умений анализировать способы решения систем уравнений); развитие не только логического, но и образного мышления, фантазии детей и их способности рассуждать.

11. Тип урока: Урок открытия нового знания.

12. Формы работы учащихся: фронтальная, работа в парах, индивидуальная

13. Необходимое оборудование: доска, экран, проектор, компьютер, документ камера, карточки самооценки.

14. Структура и ход урока

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

Регулятивные: организация своей учебной деятельности

Личностные: мотивация учения, уважение личности и её достоинства, доброжелательное отношение к окружающим

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Обеспечение мотивации учения детьми, принятие ими целей урока.

Мотивирует учащихся, вместе с ними определяет цель урока через решение систем двух уравнений первой степени с двумя неизвестными подбором, с выходом к решению систем двух уравнений первой степени с двумя неизвестными методом подстановки, акцентирует внимание учащихся на значимость темы

Работают устно, повторяют пройденный ранее материал. Формулируют тему урока. Записывают дату в тетрадь, тему и цель урока.

Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме, умение самостоятельно формулировать цели.

Регулятивные: целеполагание, планирование

Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса.

3. Применение знаний и умений в новой ситуации

Показать разнообразие систем двух уравнений первой степени с двумя неизвестными

Организация и контроль за процессом решения систем двух уравнений первой степени с двумя неизвестными методом подстановки

Решают систему двух уравнений совместно с учителем. Формулируют алгоритм решения систем двух уравнений первой степени с двумя неизвестными методом подстановки. Работают в парах над поставленными задачами. Защита и представление решения.

Познавательные: формирование интереса к данной теме.

Личностные: формирование готовности к самообразованию.

Коммуникативные: умение высказывать свою точку зрения, с уважением относиться к мнению других;

умение договариваться, находить общее решение практической задачи;

умение оформлять свои мысли в устной и письменной форме;

Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата.

4.Выполнение упражнений, закрепление навыков

Работа у доски и на местах

Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме.

Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата.

5. Контроль усвоения, обсуждение допущенных ошибок и их коррекция.

Дать качественную оценку работы класса и отдельных обучаемых.

Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок.

Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения систем двух уравнений первой степени с двумя неизвестными методом подстановки

Личностные: формирование позитивной самооценки

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;

Регулятивные: умение выделить и осознать то, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;

6. Информация о домашнем задании

Обеспечение понимания детьми содержания и способов выполнения домашнего задания

Дает комментарий к домашнему заданию

Учащиеся записывают в дневники задание.

7 . Рефлексия (подведение итогов урока)

Дать количественную оценку работы учащихся

Подводит итоги работы групп и класса в целом.

Учащиеся сдают карточки самооценки.

Регулятивные: оценивание собственной деятельности на уроке

1. Организационный этап

Учитель приветствует учащихся, проверяет их готовность к уроку.

У каждого из вас на столах лежат карточки самооценки. Подпишите их. В течение урока мы с вами будем выполнять различные задания. По окончанию решения каждой задачи, вы должны оценить свою работу

Учащиеся слушают учителя, оформляют карточки.

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

1.Что нового мы узнали на предыдущих уроках? Приведите примеры уравнений первой степени с двумя неизвестными. Назовите коэффициенты при неизвестных и свободный член. Что называют решением уравнения первой степени с двумя неизвестными?

2. Составьте уравнение первой степени с двумя неизвестными по данным

_{3. Покажите, что пара чисел является решением уравнения}

_{4. Назовите коэффициенты при неизвестных и свободные члены уравнений системы:}

_{5. Какая пара чисел , является решением системы:}

6. Каким способом мы решили задачу из предыдущего пункта о возрасте брата и сестры? (Слайд №2)

Возможно ли таким способом, решить например такую систему уравнений? Удобен ли этот способ? Чему вы хотели бы научиться на этом уроке?

Итак, тема нашего урока: (Слайд №3)

Решение систем двух уравнений первой степени с двумя неизвестными методом подстановки

Наша цель на уроке?

Научится решать системы двух уравнений первой степени с двумя неизвестными, составить алгоритм решения системы двух уравнений первой степени с двумя неизвестными, научиться использовать его при решении упражнений

Итак, приступаем к решению системы двух уравнений первой степени с двумя неизвестными.

Решить в классе:

_{Пример 2.} Метод решения остаётся тем же.

Выведем алгоритм решения системы двух уравнений первой степени с двумя неизвестными способом подстановки

Алгоритм решения системы двух уравнений первой степени с двумя неизвестными методом подстановки

Одно из неизвестных ( например у ), выразить через другое ( выбираем удобную неизвестную, с коэффициентом 1 или 2 ) неизвестное из любого уравнения системы

Подставляем полученное выражение вместо у , в другое уравнение системы

Решаем полученное уравнение с одним неизвестным х

Подставив найденное значение в формулу, для у , найдем

Пара чисел и будет единственным решением системы.

(Слайд №4) выдать каждому ученику

1.Уравнение первой степени с двумя неизвестными и системы двух уравнений первой степени с двумя неизвестными. Приводят примеры, называют коэффициенты

Решением уравнения называют пару чисел _{, которая обращает уравнение в верное равенств}

2,3,4,5,6 учащиеся предлагают свои решения. По окончании работы над каждым примером, оценивают результат своей деятельности на листах самооценки.

Отвечают на поставленные вопросы

Предполагаемый ответ: методом подбора.

Нет, не очень удобен.

Решать системы двух уравнений первой степени с двумя неизвестными

Формулируют тему и цель урока, записывают в тетради дату и тему урока.

Предполагаемый ответ: н аучится решать системы двух уравнений первой степени с двумя неизвестными, составить алгоритм решения системы двух уравнений первой степени с двумя неизвестными методом подстановки, научиться использовать его при решении упражнений

Учащиеся решают систему,

записывают решение задачи в тетрадь.

По окончании работы над каждой системой, оценивают результат своей деятельности на листах самооценки.

Выводят алгоритм решения системы двух уравнений первой степени с двумя неизвестными

3. Применение знаний и умений в новой ситуации

Ну а теперь — работа в парах.

Решают системы уравнений на выбор самостоятельно в парах (слайд №5)

Решаем из учебника: №698 (б, г,е )

Учащиеся в группах выполняют решение выбранных задач.

Ребятам предлагается работа в парах, предлагаются на выбор несколько систем

В классе 12 пар. Задачу необходимо решить, оформить решение и «защитить» свое решение (используется документ камера)

По окончании работы над каждым примером, оценивают результат своей деятельности на листах самооценки.

У доски отвечает один ученик, остальные оформляют решение задачи в тетради

оценивают результат своей деятельности на листах самооценки.

4 . Контроль усвоения, обсуждение допущенных ошибок и их коррекция

Наш урок подходит к концу. Давайте обсудим: какие задачи вызвали у вас затруднения и почему?

Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения задач.

5. Информация о домашнем задании

Домашнее задание: (Слайд №6)

на выбор и по желанию один пример из №699

2. Придумать и решить задачу, при решении которой надо будет применить систему двух уравнений

Учащиеся получают домашнее задание, записывают в дневник, выбирают задание.

6. Рефлексия (подведение итогов урока)

1. Понятен ли способ подстановки при решении систем двух уравнений первой степени с двумя неизвестными?

2. Что вызвало затруднения?

3. Что сегодня на уроке было интересно?

4. Где можно встретиться с необходимостью решать такие системы?

Собираются карточки самооценки и выставляются оценки за работу на уроке.

Видео:Алгебра 7 класс (Урок№48 - Решение систем двух линейных уравнений с двумя неизвестными.)Скачать

Конспект урока алгебры в 7 классе по теме : «Решение систем линейных уравнений с двумя переменными.»

Тип урока: закрепления знаний и отработки умений

Цель урока: сформировать у учащихся практические умения решения систем линейных уравнений. Применять систем линейных уравнений к решению задач.

Задачи урока:

• создать условия для обобщения, углубления и закрепления основных знаний, приобретенных за время изучения темы;
• использование их при решении текстовых задач;
• совершенствование практических умений учащихся.

• развитие познавательных процессов учащихся таких как: внимание, память, речь, мышление, восприятие;
• развитие интеллектуальных и творческих способностей обучающихся
• совершенствование у обучающихся логических операций анализа, синтеза, сравнения, систематизации и обобщения;
• развитие воли, эмоций, интересов, способностей и личностных качеств учащихся.

• воспитать у учащихся культуру поведения, чувство ответственности;
• Побуждать учеников к самоконтролю, вызывать у них потребность в обосновании своих высказываний.
• воспитывать коммуникативные компетентности обучающихся, толерантное отношение к окружающим, чувство доброты, сострадания, желание прийти на помощь, аккуратность, дисциплинированность.
• привить интерес к предмету.

Просмотр содержимого документа
«Конспект урока алгебры в 7 классе по теме : «Решение систем линейных уравнений с двумя переменными.»»

МОУ «Степано – Крынская школа»

Донецкой Народной Республики

Конспект урока алгебры в 7 классе

по теме : «Решение систем линейных уравнений с двумя переменными.»

Подготовила и провела

Тип урока: закрепления знаний и отработки умений

Цель урока: сформировать у учащихся практические умения решения систем линейных уравнений. Применять систем линейных уравнений к решению задач.

создать условия для обобщения, углубления и закрепления основных знаний, приобретенных за время изучения темы;

использование их при решении текстовых задач;

совершенствование практических умений учащихся.

развитие познавательных процессов учащихся таких как: внимание, память, речь, мышление, восприятие;

развитие интеллектуальных и творческих способностей обучающихся

совершенствование у обучающихся логических операций анализа, синтеза, сравнения, систематизации и обобщения;

развитие воли, эмоций, интересов, способностей и личностных качеств учащихся.

воспитать у учащихся культуру поведения, чувство ответственности;

Побуждать учеников к самоконтролю, вызывать у них потребность в обосновании своих высказываний.

воспитывать коммуникативные компетентности обучающихся, толерантное отношение к окружающим, чувство доброты, сострадания, желание прийти на помощь, аккуратность, дисциплинированность.

привить интерес к предмету.

Основные методы: устный опрос, взаимопроверка, беседа, письменные упражнения, групповая, коллективная работа.

Оборудование : мультимедийный проектор, ноутбук, экран, карточки.

1. Организационный момент. – 1 мин

2.Проверка домашнего задания. – 1 мин

3. Мотивация урока. – 1 мин

4. Сообщение темы и цели урока. — 1 мин

5. Мотивация учебной деятельности. – 1 мин

6.Актуализация опорных знаний. – 10 мин

7. Закрепление изученного материала. — 24

8.Домашнее задание. – 1 мин

9.Итог урока. – 5 мин

Добрый день, добрый час!
Как я рада видеть вас.
Друг на друга посмотрели
И тихонечко все сели.

Мы сюда пришли учиться,
Не лениться, а трудиться.
Работаем старательно,
Слушаем внимательно!

(Психологический настрой учащихся на продуктивную творческую работу.

2.Проверка домашнего задания. (Учитель сбирает тетради)

Эта история произошла давным – давно. В древнем городе жил добрый мудрец и злой человек, который завидовал славе мудреца. И решил он придумать такой вопрос, чтобы мудрец не смог на него ответить. Пошёл он на луг, поймал бабочку, сжал между сомкнутыми ладонями и подумал: « Спрошу – ка я: о, мудрейший, какая у меня бабочка – живая или мертвая? Если он скажет, что мертвая, я раскрою ладони – бабочка улетит, а если скажет, что живая, я сомкну ладони, и бабочка умрёт». Так завистник и сделал. Поймал бабочку, посадил между ладоней, отправился к мудрецу и спросил его: «Какая у меня бабочка живая или мертвая»? Мудрец ответил: «Всё в твоих руках!»

Как часто, ребята, нам кажется, что ничего не понимаю, ничего не знаю, ничего не решу! Но я хочу повторить слова мудреца «все в твоих руках». Пусть эти слова будут девизом нашего урока.

4. Сообщение темы и цели урока

— Дорогие ребята! Однажды польский писатель Станислав Лем сказал, что, для того, чтобы что-то узнать, нужно уже что-то знать. (слайд 2) Скажите, пожалуйста, какие темы мы изучали на предыдущих уроках? (Ответы обучающихся)

— Какой будет тема нашего сегодняшнего урока? (Ответы обучающихся)(слайд3)

-Вы правы, тема этого урока «Решение систем линейных уравнений с двумя переменными «. — урок закрепления изученного материала.

— Запишите в тетрадях «Двенадцатое марта. Классная работа. Тема: « …..»

— Какой будет цель нашего урока? (Ответы обучающихся)

— Молодцы! Сегодня наша цель – усовершенствовать умение использовать графический способ, способ подстановки, способ сложения к решению систем линейных уравнений, проверить свое умение применять приобретенные знания к решению задач. (слайд 4)

— И поможет нам работать совет Конфуция (слайд 5)

«Чем бы Вы ни занимались в жизни, делайте это всем своим сердцем», Чтобы добиться успеха в жизни, что бы вы ни делали, делайте это с полной отдачей или не делайте вовсе.

— Скажите, сможем ли мы достичь цели урока? (Ответы обучающихся)

— Я также надеюсь, что нам всем вместе удастся добиться успеха.

5. Мотивация учебной деятельности (слайд 6)

Проанализируем логическую взаимосвязь между содержательными линиями

Алгебра

Числа; действия над числами

Выражения; преобразование выражений

Уравнения и системы уравнений

— Для чего мы знакомимся с системами уравнений, рассматриваем алгоритмы решения разными способами? (Ответы обучающихся)

— Да, эти знания нам необходимы для того, чтобы получить определенное «орудие» для самого важного – решения текстовых задач, прикладных задач, моделирования реальных процессов и явлений.

6.Актуализация опорных знаний.

Повторение базовых понятий данной темы:

Что называется системой двух линейных уравнений с двумя переменными? (Линейной системой двух уравнений с двумя переменными называется система вида

г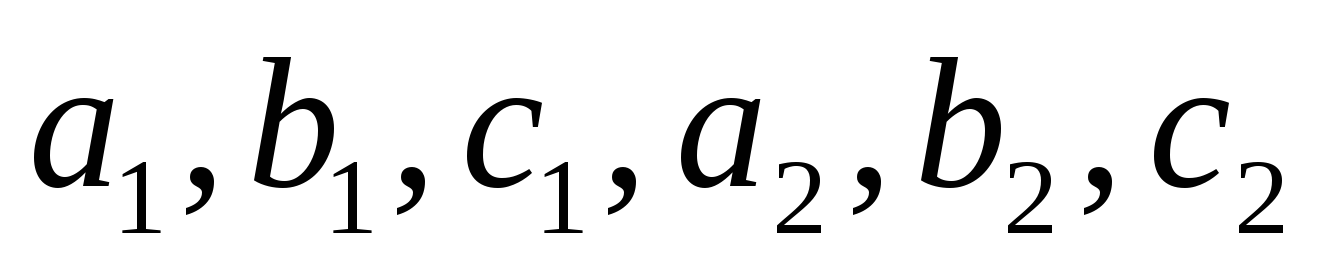де — некоторые числа (одновременно не равны нулю),

Дать определение решения системы двух линейных уравнений с двумя переменными.

(Решением системы называются пара значений (х;у), которая обращает каждое уравнение системы в верное равенство)

Что представляет собой график линейного уравнения?

(Если хотя бы один из коэффициентов a, b линейного уравнения ax+by+c=0 отличен от нуля, то графиком уравнения служит прямая линия.)

Как графически изображается решение системы двух линейных уравнений?

(Координаты точки пересечения графиков линейных уравнений являются решением системы двух линейных уравнений.)

5. Сколько общих точек могут иметь две прямые, которые лежат в одной плоскости?

1.Ни одной. 2. Одну. 3. Бесконечное множество.

6. Какова взаимосвязь между предыдущим вопросом и количеством решений системы двух линейных уравнений с двумя переменными?

Количество решений системы равно числу общих точек прямых, являющихся графиками уравнений системы.

Устный счет: «Одним взглядом» (слайд 8-12)

— Сколько решений имеет система?

— Через какую из точек проходит график уравнения ?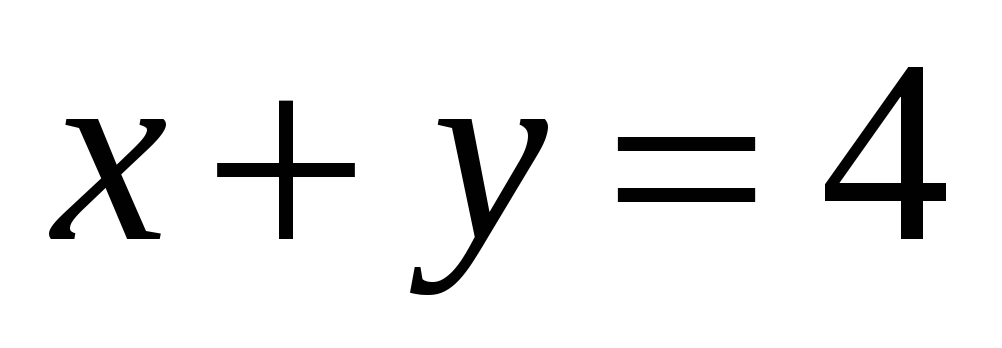

—Через какую из точек проходит график уравнения ?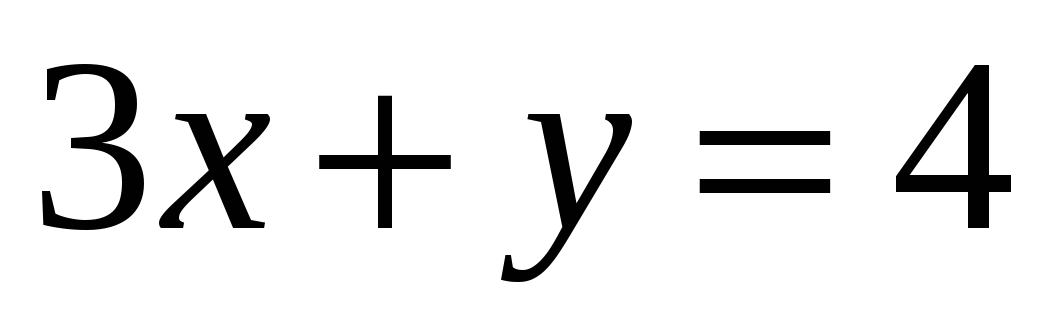

— Через какую из точек проходит график уравнения?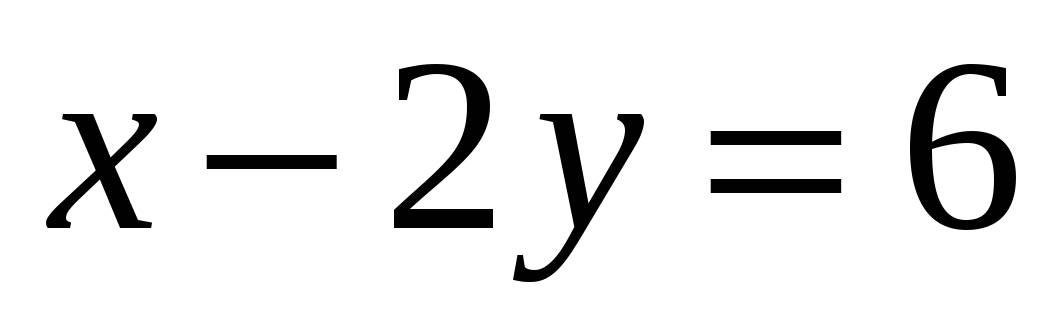

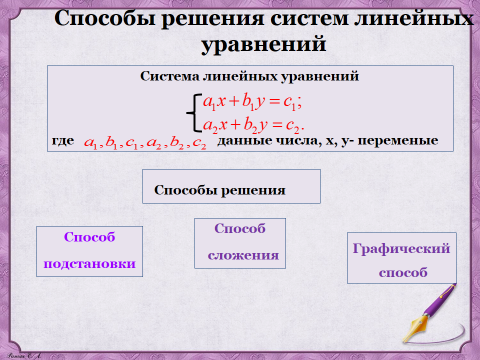
— Вспомним, какие существуют способы решения систем линейных уравнений с двумя переменными? (слайд 13)

— Сформулируйте алгоритм решения системы линейных уравнений графическим способом.

— Сформулируйте алгоритм решения системы линейных уравнений способом подстановки.

— Сформулируйте алгоритм решения системы линейных уравнений способом сложения.

— У вас на партах лежат карточки, определите каким способом удобно решить систему, и подпишите рядом с системой способ.

7. Закрепление изученного материала

Собраться вместе – это начало, держаться вместе – это прогресс, работать вместе – это успех.

(Генри Форд, американский предприниматель) (слайд14)

Решить систему уравнений с двумя переменными

1 команда- методом подстановок

2 команда- методом сложения

3 команда- графическим методом

Решить систему уравнений повышенного уровня сложности:

Ответ х=5, =8. (слайд 17 )

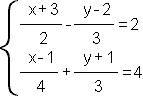
Фильтр от сигареты разлагается на 10 лет дольше, чем консервная банка. С созданием материалов, разлагающихся под воздействием света можно уменьшить период разложения фильтра в 2 раза, а консервной банки в 5 раз, тогда разница между периодами разложения будет 32 года. Найти период разложения каждого предмета.

Итог (теоритический материал) (слайд 21)

— Творческое задание. Составить три системы уравнений и решить разными способами», кроссворд по теме: «Уравнения с одной переменной и методы их решения»

Совет Конфуция по выполнению домашнего задания (слайд 23)

Когда вам покажется, что цель недостижима, не изменяйте цель —изменяйте свой план действий.

Анализ проделанной работы, выставление оценок.

Учитель: Какую цель ставили в начале урока? Достигли?

— Я предлагаю вам самим оценить свою работу на уроке отвечая на вопросы.

Чему мы будем учиться на следующих уроках? (Решать задачи с помощью систем линейных уравнений с двумя переменными)

📽️ Видео

Система уравнений. Метод алгебраического сложенияСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Решение систем уравнений методом подстановкиСкачать

Алгебра 7 класс (Урок№45 - Уравнения первой степени с двумя неизвестными.)Скачать

7 класс, 37 урок, Системы двух линейных уравнения с двумя переменными. Основные понятияСкачать

Алгебра 7 класс (Урок№47 - Равносильность уравнений и систем уравнений.)Скачать

Алгебра 7 класс. 28 октября. Решаем систему уравнений методом сложения #2Скачать

Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

7 класс, 40 урок, Системы двух линейных уравнений с двумя переменными как математические моделиСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

Алгебра 7 класс. Решение систем уравнений методом подстановкиСкачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Видеоурок ЛИНЕЙНОЕ УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать