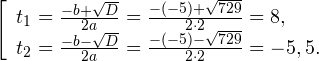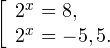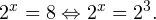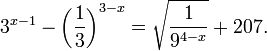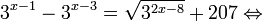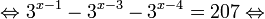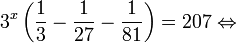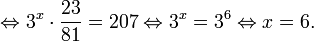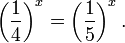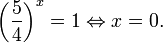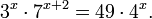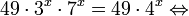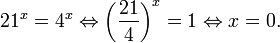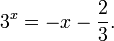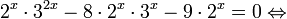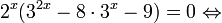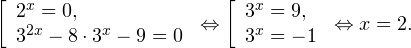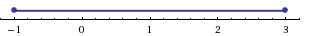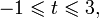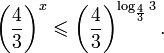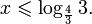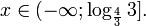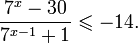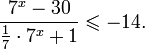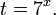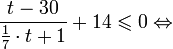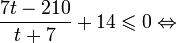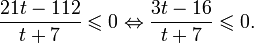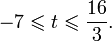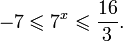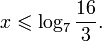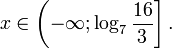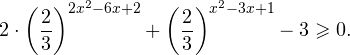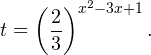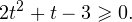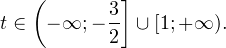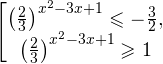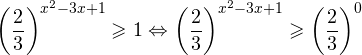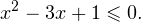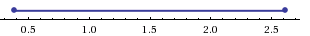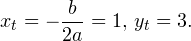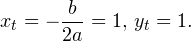Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
- Решении показательных уравнений
- Показательные уравнения и их системы
- Пример №1
- Пример №2
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- Системы простейших показательных уравнений
- Пример №7
- Пример №8
- Пример №9
- Приближенное решение уравнений
- Пример №10
- Нахождение приближенного корня с заданной точностью
- Пример №11
- Показательные уравнения и неравенства
- Показательная функция
- Что такое показательная функция?
- Решение показательных неравенств
- Урок-семинар на тему: «Показательная функция. Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ» план-конспект урока по алгебре (10 класс) на тему
- Скачать:
- Предварительный просмотр:
- 📹 Видео
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
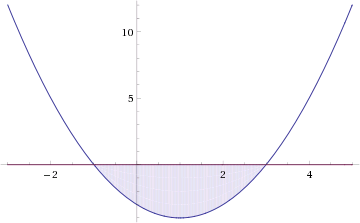
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ системы показательных неравенствСкачать

Показательные уравнения и неравенства
Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению показательных уравнений и неравенств. В вариантах ЕГЭ по математике к такому типу задач относится, в частности, задача C3. Научиться решать задания C3 важно не только с целью успешной сдачи ЕГЭ, но и по той причине, что это умение пригодится при изучении курса математики в высшей школе.
Выполняя задания C3, приходится решать различные виды уравнений и неравенств. Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике «Методическая копилка репетитора по физике и математике» в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
Прежде чем приступить к разбору конкретных показательных уравнений и неравенств, как репетитор по математике, предлагаю вам освежить в памяти некоторый теоретический материал, который нам понадобится.
Видео:Это просто! Как решать Показательные Неравенства?Скачать

Показательная функция
Что такое показательная функция?
Функцию вида y = a x , где a > 0 и a ≠ 1, называют показательной функцией.
Основные свойства показательной функции y = a x :
| Свойство | a > 1 | 0 только в показателях каких-либо степеней. Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему: Помимо этого, полезно помнить об основных формулах и действиях со степенями:
Пример 1. Решите уравнение: Решение: используем приведенные выше формулы и подстановку: Уравнение тогда принимает вид: Дискриминант полученного квадратного уравнения положителен:
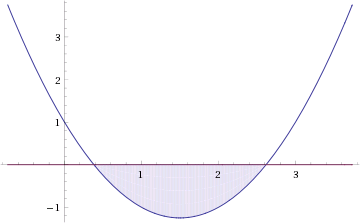
Это означает, что данное уравнение имеет два корня. Находим их: Переходя к обратной подстановке, получаем: Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе: С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию. Ответ: x = 3. Пример 2. Решите уравнение: Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 9 4 -x положительна и не равна нулю). Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней: Последний переход был осуществлен в соответствии с теоремой 1. Пример 3. Решите уравнение: Решение: обе части исходного уравнения можно поделить на 0,2 x . Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид: Ответ: x = 0. Пример 4. Решите уравнение: Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней: Деление обеих частей уравнения на 4 x , как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x. Ответ: x = 0. Пример 5. Решите уравнение: Решение: функция y = 3 x , стоящая в левой части уравнения, является возрастающей. Функция y = —x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет. Ответ: x = -1. Пример 6. Решите уравнение: Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи: Ответ: x = 2. Видео:Показательные уравнения. 11 класс.Скачать  Решение показательных неравенствПоказательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней. Для решения показательных неравенств требуется знание следующей теоремы: Теорема 2. Если a > 1, то неравенство a f(x) > a g(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 f(x) > a g(x) равносильно неравенству противоположного смысла: f(x) 2x , при этом (в силу положительности функции y = 3 2x ) знак неравенства не изменится: Тогда неравенство примет вид: Итак, решением неравенства является промежуток: переходя к обратной подстановке, получаем: Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству: Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству: Итак, окончательно получаем ответ: Пример 8. Решите неравенство: Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде: Введем новую переменную: С учетом этой подстановки неравенство принимает вид: Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство: Итак, неравенству удовлетворяют следующие значения переменной t: Тогда, переходя к обратной подстановке, получаем: Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству: Окончательно получаем ответ: Пример 9. Решите неравенство: Решение: Делим обе части неравенства на выражение: Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем: Воспользуемся заменой переменной: Исходное уравнение тогда принимает вид: Итак, неравенству удовлетворяют значения t, находящиеся в промежутке: Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая: Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе: Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству: Итак, окончательный ответ: Пример 10. Решите неравенство: Решение: Ветви параболы y = 2x+2-x 2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине: Ветви параболы y = x 2 -2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине: Вместе с этим ограниченной снизу оказывается и функция y = 3 x 2 -2x+2 , стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1. Ответ: x = 1. Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене. P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно. Видео:10 класс. Алгебра. Системы показательных уравнений.Скачать  Урок-семинар на тему: «Показательная функция. Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ» |
| Вложение | Размер |
|---|---|
| Презентация к уроку-семинару http://nsportal.ru/sites/default/files/filefield_paths/urok_-_seminar_10_klass_pokazatelnaya.docx | 263.31 КБ |
| otkrytyy_urok_pokazatelnaya_funktsiya_uravneniya_neravenstva.pptx | 844.11 КБ |
Видео:Как решать такие системы показательных уравненийСкачать

Предварительный просмотр:
Муниципальное образовательное учреждение
«Средняя общеобразовательная школа №8»
г. Железногорск Курская область
Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ»
Подготовила и провела
Кушнерева Светлана Федоровна
Тема: “Показательная функция. Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ”.
Обучающие: познакомить с заданиями разного уровня сложности, содержащими показательные уравнения и неравенства и их системы, из открытого банка подготовки к ЕГЭ. Обобщить знания и умения учащихся по применению методов решения показательных уравнений и неравенств, закрепить знание свойств показательной функции в процессе решения показательных уравнений и неравенств. Дать рекомендации для выполнения данных заданий на экзамене.
Развивающие: развивать у учащихся умение решать показательные уравнения и неравенства разной сложности, анализировать условие задачи и выбирать нужный метод решения; умение применять теоретические знания на практике; активизировать познавательную деятельность учащихся посредством использования компьютерных технологий; развивать навыки самоконтроля и самооценки, самоанализа своей деятельности.
Воспитательные: формировать умение выступать перед аудиторией с заданной темой, четко излагать свои мысли, работать самостоятельно, принимать решения и делать выводы. Воспитывать внимательность и упорство при решении задач, стремление к самообразованию и самосовершенствованию, осознание учащимися социальной, практической и личной значимости учебного материала по изучаемой теме.
1.Проектор и презентации учителя и учащихся по теме “ Показательная функция. Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ ”:
2.Схемы-кластеры для учащихся
I. Организационный момент. Сообщение темы, цели и задач урока.
Учитель: — Сегодня мы проведем урок-семинар.
Слайд 2 (Эпиграф)
Эпиграфом к уроку я взяла восточную мудрость: “Приобретать знания — храбрость, приумножать их — мудрость, а умело применять — великое искусство”. Вот и мы сегодня постараемся найти применение знаниям, полученным на уроках математики.
Чтобы определить, какие темы будут рассмотрены на уроке, вы должны ответить на вопросы и вставить слова в кружки схемы-кластера.
Слайд 3 (Кластер)
— Как называется икс в степени с основанием а? (Показатель)
— Какие математические понятия связаны с понятием «показатель»? (Показательная функция, показательные уравнения, показательные неравенства)
Слайд 4 (Тема урока)
Итак, тема нашего урока: “Показательная функция. Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ”. Цель – рассмотреть задания разного уровня сложности и подготовиться к ЕГЭ по данной теме, связать изученный материал с тем, что ждет вас на экзамене. В течение урока я дам рекомендации, как лучше выполнять задания. Для повторения основного теоретического материала к семинару вам были предложены темы:
«Показательная функция, ее свойства и график».
«Показательные уравнения и неравенства и основные методы их решения»
На уроке мы прослушаем выступления по данным темам, рассмотрим примеры применения этого материала на экзамене. У каждого из вас на парте есть данная схема. К концу урока вы должны записать в нее методы решения показательных уравнений и неравенств.
II. Основная часть урока
Учитель: — А сейчас прослушаем первое выступление.
Тема: «Показательная функция, ее свойства и график»
«Показательные уравнения. Методы решения показательных уравнений»
Учитель: — Показательные уравнения, решаемые методом уравнивания показателей, встречаются в базовом уровне под № 7 , а в профильном уровне под №5. Под этими номерами могут также встретиться уравнения других видов: иррациональное, логарифмическое, рациональное, квадратное или линейное.
Вот примеры из демонстрационных вариантов 2017 года:
Как видите, уравнения мало чем отличаются. Их можно решить даже устно. Но на экзамене рекомендуется все же сделать краткую запись решения или проверку: 3 х-3 =81; 3 х-3 = 3 4 ; х-3=4; х=7. Проверка: 3 7-3 =3 4 =81.
Обратите внимание на то, что корень уравнения должен быть один! Если, например, вы решаете квадратное уравнение, получаете два корня, то в ответ идет только корень, удовлетворяющий условию задания.
На экзамене очень важно правильно распределить время. На первые, более простые задачи, отводится около 20 минут. Затем скорость лучше уменьшить. Внимание, как правило, ослабевает. Из-за этого допускается много ошибок.
Слайд 5(Самостоятельная работа. Задания)
Учитель: — Предлагаю вам небольшую самостоятельную работу на 5 минут
📹 Видео
Системы показательных уравнений и неравенств. Практика. Видеоуроки 13. Алгебра 10 классСкачать

Как решать системы показательных уравнений. Урок№ 27Скачать

Системы показательных уравнений и неравенств. Видеоурок 13. Алгебра 10 классСкачать

Как решать Показательные Уравнения? (часть 2)Скачать

ЕГЭ. Математика. Показательные уравнения, неравенства и их системы. ПрактикаСкачать

§14 Системы показательных уравнений и неравенствСкачать

Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать

Показательные неравенства. 11 класс.Скачать

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

Показательные уравнения за 50 минут | Математика ЕГЭ 10 класс | УмскулСкачать

системы показательных уравнений и неравенствСкачать

Как решать показательные неравенства | Часть 2Скачать

Показательные неравенства за 50 минут | Математика ЕГЭ 10 класс | УмскулСкачать











































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);











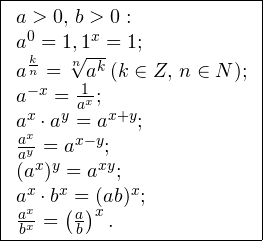 0,, b>0: \ a^0 = 1, 1^x = 1; \ a^<frac>=sqrt[n]
0,, b>0: \ a^0 = 1, 1^x = 1; \ a^<frac>=sqrt[n] 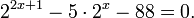
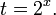
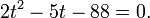
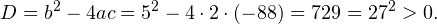 0. ]» title=»Rendered by QuickLaTeX.com»/>
0. ]» title=»Rendered by QuickLaTeX.com»/>